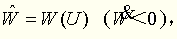企业核心竞争力评价指标体系构建

　　1、评价指标的无量纲化处理。无量纲化是数据的标准化、规格化，它是通过数学变换来消除原始变量量纲影响的方法。反映企业核心竞争力的各项指标都有不同的量纲，应首先对评价指标进行无量纲化处理。评价指标的无量纲化处理实质是将评价指标的原始值转化为评价值的过程。假定我们所研究的定量指标的实际值转化成不受量纲影响的指标评价值时，二者之间呈线性关系，指标数实际值的变化引起指标评价值一个相应的比率变化。利用隶属函数，构造下列无量纲化函数：
　　2、指标权重确定的数学模型。在多级模糊综合评价中，权重值的确定直接影响着综合评价的结果，权重值的变化会引起被评对象优劣程度的变化。因此，科学地确定指标权重在多级模糊综合评判中举足轻重。企业核心竞争力评价指标体系具有多级结构的特点，同时在评价指标体系中，为准确、综合地反映企业的综合发展能力，必须将定性指标与定量指标综合考虑，有机地结合。层次分析法对于含有定性、非量化因素的评价问题，可以统一处理综合评价中的定性和定量因素，通过专家的判断和选择，对评价指标的重要性程度进行量化、排序，计算也简便。所以，多级结构层次分析法较为适合于确定企业核心竞争力评价指标的权重。
　　（1）构建指标权重的判断矩阵。指标体系建立后，上下层次指标间的隶属关系就被确定了。为了比较科学、准确的确定各指标的权重，使层次分析用到的数据具有较高的权威性和可靠性，需要考评专家小组对同一层次指标进行模糊评价，两两比较。为了将比较判断定量化，层次分析法引入见表2所示的1-9比率标度法，并写成矩阵形式，即构成所谓判断矩阵A=（aij）m×n。
　　（2）计算指标权重。计算各层元素对系统目标的合成权重，并对此进行总排序，以确定递阶结构图中最底层各个元素在总目标中的重要程度。
　　（3）计算判断矩阵A的最大特征值λmax，并进行一致性检验。将计算出的最大特征根λmax导入公式进行一致性检验，并通过。具体公式如下：
　　R·I的取值范围见表3。（表3）
　　如果C.R＜0.1，则n阶判断矩阵A的一致性可以接受。
　　（4）指标权重的综合排序向量。根据各位专家给定的判断矩阵，依次计算各目标层指标的权重向量，然后对所有专家给出的权重向量进行综合处理，计算指标体系中对于各目标层指标的综合排序向量。采用几何平均综合排序向量方法对多个判断矩阵进行计算，得到权重的综合排序向量。出于理论分析及实际应用的目的，企业核心竞争力的评价需要有一套量化的指标体系，考虑到企业核心竞争力的评价具有模糊性和主观性的特点，量化指标的确定和获得尚有一定的难度。需要说明的是，尽管层次分析法（AHP）克服了以往在确定绩效考核指标权重过程中主观因素影响太大、以偏概全的弊端，将定性问题定量化，但由于影响绩效考核的因素过于庞杂，而且有些无法进行量化。因此，企业在进行层次分析法构建绩效考核的指标体系时，仍然需要视具体情况与其他方法结合使用，以保证绩效考核的结果客观准确。
 
　　主要参考文献：
　　[1]李显君.国富之源——企业竞争力[M].北京：企业管理出版社，2002.
　　[2]刘伟东，陈凤杰.中小企业现代经营[M].大连：东北财经大学出版社，2002.
　　[3]杜栋，庞庆华，吴炎.现代综合评价方法与案例精选[M].北京：清华大学出版社，2004.