理性房地产开发企业的非理性决策
内容摘要:文章使用卡尼曼的“前景理论”初步分析了理性的房地产开发在市场竞争中出现的非理性行为,进而导致了市场结构的非理性均衡。
关键词:房地产开发企业 理性博弈 非理性决策前景理论
房地产和住宅市场是一个复杂的系统;作为重要组成部分的新房市场对其影响巨大。在北京房地产和住宅市场日益成熟的今天,竞争使开发企业占据在新房市场的不同层次上可将其简单的划分为高端、中端和低端市场。处于高端市场的开发企业向市场提供高档商品房、别墅等项目,处于中低端市场的开发企业向市场提供普通商品房或适用房等项目。在面对市场需求结构变化后,处于不同层次的房地产开发企业在竞争博弈过程中出现的非理性决策行为导致了市场结构的失衡。
博弈模型
本文设定在高端市场开发企业为甲类企业(以下简称为甲),在中低端市场的开发企业为乙类企业(以下简称为乙)。假设如下:在博弈模型中甲乙均是理性人,即追求自身效用的最大化;甲乙进行的是非合作博弈;在市场机制失灵出现开发过热、房地产泡沫或结构失衡时,政府实施的宏观调控政策符合甲乙的长期利益。在此假设条件下,由于房地产开发周期长区域性强等特点,甲乙之间的博弈可视为静态博弈。按照不完全信息静态博弈原理可知,每个参与人只知道另一参与人类型的概率分布而不知道其真实类型,他不可能准确地知道另一参与人实际上会选择什么策略;但他能正确地预测到其他参与人的策略是如何依赖于各自的类型。他决策的目标就变为给定自己的类型和别人的类型的情况下,最大化自己的期望效用。
假设住宅市场需求结构发生了较大变化,乙获得高利润的可能性是x;住宅市场需求结构发生较小变化,乙获得低利润的可能性是(1-x)。
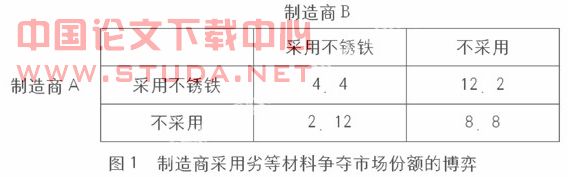
甲乙博弈策略及支付表达式:
r1、c1:甲成功进入中低端市场开发项目获得的收益和用于项目建设的必要成本;
r2、c2: 乙在中低端市场开发项目获得的收益和用于项目建设的必要成本;
c12:甲进入乙斗争使甲付出的额外成本;c21:甲进入乙斗争使乙付出的额外成本;
c11:甲进入乙默许中低端市场竞争加剧使甲支出的额外成本;
c22:甲进入乙默许中低端市场竞争自然加剧使乙支出的额外成本;
表中0表示甲不进入在中低端市场获得的效用为0;
字母大小写含义是:大写代表处于住宅市场需求结构发生较大变化条件下;小写代表处于住宅市场需求结构发生较小变化条件下。
甲的策略为δ=(α,1-α),即甲以α的概率选择进入,以1-α的概率选择不进入;
乙的策略为γ=(β,1-β),即乙以β的概率选择默许,以1-β的概率选择斗争;
(0≤α,β≤1)。
甲的效用函数U1=α{[(R1-C1-C11)x+ (r1-c1-c11)(1-x)]β+[(R1-C1-C11-C12)x+(r1-c1-c11-c12)(1-x)](1-β)}+(1-α)×0
对上述效用函数求导,得到甲最优化的一阶条件,并解为:
β°=[(R1-C1-C11-C12)x+ (r1-c1-c11-c12)(1-x)]/[- C12x-c12(1-x)]
乙的效用函数V=β{[(R2-C2-C22)x+(r2-c2-c22)(1-x)]α+[(R2-C2)x+(r2-c2)(1-x)] (1-α)}+ (1-β){[(R2-C2-C22-C21) x+(r2-c2-c22-c21)(1-x)] α+[(R2-C2)x+(r2-c2)(1-x)]( 1-α)}
对上述效用函数求导,得到乙最优化的一阶条件α[C21x+c21(1-x)]=0,并解为:
αo=ε(0≤ε≤1)
即上述非合作不完全信息静态博弈混合策略的纳什均衡解为:
αo=ε (1)
βo=[(R1-C1-C11-C12)x+(r1-c1-c11-c12)(1-x)]/[- C12x-c12(1-x)](2)
混合策略纳什均衡解的存在性:
C21x+c21(1-x)=0,即:x=c21/(c21-C21) (3)
[(R1-C1-C11-C12)x+(r1-c1-c11-c12)(1-x)]<[-C12x-c12(1-x)]
即 x>(r1-c1-c11) /[(r1-c1-c11)-(R1-C1-C11)] (4)
只有当(1)、(2)式成立时混合策略的纳什均衡解才得以存在。(1)表示甲只能以概率为ε选择进入,或者说有ε比例的企业从高端市场进入中低端市场。(2)表示乙以β°的概率选择默许,或者说在中低端市场有β°比例的企业选择默许。混合策略纳什均衡是: αo=ε,β°=[(R1-C1-C11-C12)x+(r1-c1-c11-c12)(1-x)]/[- C12x-c12(1-x)]。(4)式中[(r1-c1-c11)-(R1-C1-C11)]通常情况下为负值,所以(4)式通常情况下成立;但(3)式中(c21-C21) 通常情况下为正值,所以(3)式通常情况下不成立;则混合策略的纳什均衡解不存在。若(3)式不成立,由乙最优化的一阶条件α[C21x+c21(1-x)]=0可知αo=0,存在的是纯策略的纳什均衡解“甲不进入,乙任意”。欲使(3)式成立,则需要改变甲对β、x和(c21-C21) 等值的认知;否则在现实中形成博弈“僵局”,使得房地产供给结构不能及时适应需求结构的变化,造成房地产市场的结构性失衡。
就上述博弈模型自身而言,即使在混合策略的纳什均衡解存在的条件下,甲是否选择进入还需进一步考虑机会成本和进入前后获取效用增量函数ΔU的风险。此处ΔU= U1-U0,U0代表甲固守高端市场的效用函数。
甲对β、x、C21、c21和ΔU等值的准确判断依赖于贝叶斯定理大数法则,这不仅要使用大样本的所有信息,也需要利用先验信息(以往存在的知识)。这意味着需要大量的有关住宅市场信息,对甲来说要花费大量的信息搜寻成本。
在信息搜集和积累过程中,客观上由于房地产相关政策不完善和制度的不透明以及其他房地产开发的前期工作的隐蔽性和建设周期长等诸多原因,使得甲收集的信息的准确性降低和时效性变差;并且在现实中,甲处于高端市场,在不断的开发中逐步取得学习的优势,在竞争中更容易建立关于高端市场的信息优势。主观上,对乙而言甲选择不进入策略是乙期望效用最大化的理想条件,于是乙就会有意隐瞒信息以降低甲对β、x、C21、 c21和ΔU等值的准确判断。这样导致甲建立的关于市场结构和各特征变量的初始值就在很大程度上带有甲对高端市场的偏好,对进入中低端市场获取利润正增量的把握性降低,增大了进入的风险。
卡尼曼与特韦尔斯基认为,人们在对不确定事物进行判断和估计的时候通常会设定一个初始值,然后根据反馈信息对这个初值进行修正。随着社会、人口、经济的,房地产市场需求结构处于不断的变化中,种种变化信息所反映的增量值不断修正着甲的初始值。由于甲对高端市场的偏好,再加上上述的主客观原因,在高端市场仍能够带来较高利润水平时,他对高端市场的诸多变化较之中低端市场的要敏感的多,于是造成这种持续修正过程也是非理性占较大比重的决策过程。
卡尼曼“前景理论”(Prospect Theory)的三个基本原理:大多数决策个体在面临获得的时候是风险规避的;大多数决策个体在面临损失的时候是风险偏爱的;决策个体对损失比对获得更敏感。同时卡尼曼和特韦尔斯基的研究表明,在不确定性条件下,人们的偏好主要是由增量而非总量决定的,效用函数对正的增量是凹的,对负的增量是凸的。这反映了人们在面临亏损时不是“风险厌恶”者,而是“风险追求”者。
从需求上看,2003年的北京住宅市场的总体趋势是:购房主体低龄化,低总价、中小户型需求潜力巨大;市场中坚力量萎缩导致中档定位的项目将更加艰难,高端市场(这里主要指高档商品房和别墅)基本上维持原有的发展状态,由于别墅用地的限制,供给相对固定,从供求关系的角度来讲,高档市场还有一定的成长机会和空间。此时对甲来说,如果高端市场利润有所下降,经过修正的特征变量x 、(c21-C21)和ΔU的正增量对他的效用函数ΔU是凹的,并且此时由于甲对高端市场的偏好使甲选择进入策略的风险依然很大。根据原理(1),此时甲是风险规避的,那么即使在市场需求结构发生较大变化时,他选择比较稳妥的获利方案,即采取不进入策略。从另一个角度说,如果高端市场利润略有上扬,甲的效用函数ΔU对这个负的ΔU增量是凸的,此时放弃高端市场相当于是一种损失。根据原理(2),此时甲是风险偏爱的,短期内无视市场的变化,采取不进入的策略。以上的分析也符合原理(3)。
依据市场调查显示,北京高端市场仍然有大量项目在建和上市。于是整个房地产市场的结构性失衡问题难以解决。
结 论
政府在遵循理性和非理性决策的客观的基础上,必须出台相关政策,以改变甲在不确定的情况下对市场结构的认知并使其产生偏好逆转,进而使其开发行为符合宏观调控的需要。
资料:
1.张维迎,博弈论与信息经济学[M]上海人民出版社,1996
2.瑞典皇家院,[P]2002年经济学诺奖公告,2002.10
3.易宪容、诺贝尔奖得主卡尼曼:在理性与非理性间徘徊[N],经济时报,2002.10
4.北京中原市场研究部,[R]北京楼市新趋势,2003.6.8
5.九力营销顾问公司,[R]2003北京住宅市场需求研究报告,2003.6.10