房地产开发商与施工企业工程款的博弈分析

【摘要】本文利用博弈论的分析方法，针对房地产开发市场上的两个最主要的利益主体房地产开发商和施工之间关于工程款的市场行为进行了博弈分析，可以为房地产开发商、施工企业、政府部门等提供一定的决策，也为房地产市场体系的建设提出一些建议。

　　【关键词】房地产开发商 施工企业 博弈
　　
　　一、概述
　　
　　建设工程领域的工程款问题是党中央国务院高度重视的一项工作，解决欠款问题不仅可以促进建筑业的健康，而且可以有力地保护人民群众的利益。从2004年到2006年，用三年的时间基本解决工程欠款问题和农民工工资问题，是本届政府的一项任务。一系列行之有效的政策措施的出台，加快了这项工作的实施。但是应该看到，部分地区清欠进度滞后，边清边欠问题仍然存在，预防与惩治拖欠的法规制度还有待完善。
　　建筑工程项目从前期的可行性研究到工程最后发挥效益，是一个涉及许多利益相关方的过程。这些利益相关方包括：施工企业、开发商、购房者、设计单位、监理单位、行政主管部门等。因此，在这个过程中，必然会涉及多方的博弈。但是，施工企业和开发商是最为重要的两个参与人，工程款项产生拖欠之后，双方行为产生的相互影响是很值得研究的。所以，本文运用博弈论的方法就房地产开发商和施工企业两方关于工程款问题进行博弈分析。
　　
　　二、房地产开发市场中的博弈
　　
　　作为房地产开发市场上最重要的博弈双方来说，开发商和施工企业在追求各自利益最大化的过程中会产生相互的影响，而这种影响又会体现到他们行为的不同。根据博弈的假设条件、信息结构、行动顺序、简化条件等的不同，可以将房地产开发商和施工企业的博弈过程分为：完全信息的静态博弈过程、以完全信息静态博弈为阶段博弈的重复博弈过程（也就是完全信息动态博弈）等，下面就房地产开发项目过程中常见的开发商与施工企业之间经常产生矛盾的工程款问题来分析。
　　
　　1、完全信息静态博弈
　　（1）假设条件。博弈双方都符合理性人假设；博弈双方都有关于自己和对方的完全信息；博弈双方是一次博弈。
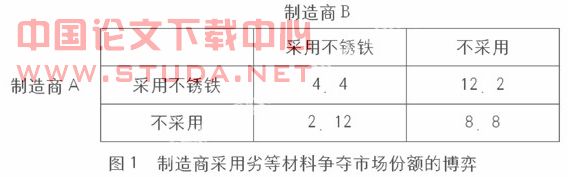
　　（2）博弈模型具体化。博弈双方：Ai，i=1,2（1表示开发商，2表示施工企业）；双方的策略空间：Si，i=1,2（房地产开发商两种策略：及时拨付工程款；延期付款。施工企业两种策略：积极施工；不积极施工）。
　　
　　F表示应支付的工程款；I1表示应支付工程款的利息；I2表示房地产开发商利用工程款进行其它投资的收益或者延期付款的利息；C代表施工企业因不积极施工而节约的成本；G表示符合要求的工程的价值（积极施工）；B表示不符合要求工程的价值（不积极施工）。
　　(3)博弈的纳什均衡。该博弈有唯一稳定的解，即有唯一的纯策略纳什均衡（不积极施工，延期付款），就是说，在该博弈中，施工企业的最佳策略是不积极施工，这样可以降低投入，降低施工成本，从而获得最大程度的利润；开发商的最佳策略是延期付款，获得资金利用上的优势。这个均衡对于房地产开发商和施工企业来说都是理性的选择，但是对于这个集体却是最坏的结果，也就是施工企业积极施工，开发商及时付款时的得益F+I1+G。
　　
　　2、有限次重复开发商与施工企业的博弈
　　动态博弈的特征是各博弈方是先后、依次进行选择或行动，因此在动态博弈中可能不止一次行为，所以每个博弈方在一个动态博弈中就可能有多个甚至无限个博弈阶段。重复博弈就是博弈的多次重复构成的博弈过程，这个重复多次的博弈就称为原博弈。
　　（1）假设条件。博弈双方都符合理性人假设；博弈双方都有关于自己和对方的完全信息；博弈双方是有限次重复博弈。
　　（2）有限次重复博弈的均衡。如果将上述讨论的完全信息静态博弈作为原博弈进行有限次重复，因为原博弈有唯一的纯策略纳什均衡，所以各博弈方的总得益为原博弈的整数倍，平均得益等于原博弈中的得益，也就是开发商和施工企业在博弈的每个阶段都采用一次博弈时的策略。
　　同样，在有限次重复博弈下，均衡是低效率的，没有实现集体的最大利益。
　　

　　3、无限次重复开发商与施工的博弈
　　如果博弈问题不是经过一定次数重复以后就肯定会结束，而是似乎会永远重复下去，这样的重复博弈称为无限次重复博弈。
　　（1）假设条件。博弈双方都符合理性人假设；博弈双方都有关于自己和对方的完全信息；博弈双方是无限次重复博弈；折扣系数是δ，δ=1/（1+r），r是一定期限内的市场利率。
　　（2）无限次重复博弈的均衡。与有限次重复博弈相同，试图合作和惩罚不合作也是无限次重复博弈能实现较理想的结果的关键。也就是博弈双方都是先试图合作，在第一次时无条件选择积极施工（或及时付款），一旦发现对方不合作（延期付款或不积极施工），则也用不合作报复，改变自己的策略，迫使对方也会选择相应的策略，结果是双方都取得较小的得益，即假设双方都采用触发策略。
　　首先，假设施工企业采用触发策略，即施工企业试图与开发商合作，在第一阶段的策略是积极施工。对于开发商来说，如果开发商每个阶段都积极配合，即及时付款，那么总得益V= G/（1-δ）；如果开发商在第一阶段延期付款，那么它会受到惩罚，因此总得益
　　V'=G+I₂）+（B+I₂）*δ+（B+I₂）*δ²……
　　=（G+I₂）+（B+I₂）*δ/（1-δ）。
　　当V≥V'，开发商会选择及时付款，即G/（1-δ）≥（G+I₂（B+I₂）*δ/（1-δ）时，此时δ≥I₂/（G- B）。………………(1)
　　接着，假设开发商采用触发策略，即开发商试图与施工企业合作，在第一阶段的策略是及时付款。对于施工企业来说，如果施工企业每个阶段都积极配合，即施工企业积极施工，那么他的总得益V0=（F+I₁）/（1-δ）；而如果开发商在第一阶段不积极施工，那么他会受到惩罚，因此总得益
　　V0'=（F+I₁+C）+（F+C）*δ+（F+C）*δ²+……
　　=（F+I₁+C）+（F+C）*δ/（1-δ）。
　　当V0≥V0'时，施工企业会选择积极施工，即（F+I₁）/（1-δ）≥（F+I₁+C）+（F+C）*δ/（1-δ）时，此时δ≥C/I₁。…………(2)
　　若假设G-B＜I₁，同时由（1）、（2）式得出，折扣系数δ≥I₂/（G-B）。
　　同时注意，C2，这是因为C是施工企业因偷工减料等原因而非正常节约的成本。
　　由此看出，在房地产开发商和施工企业的无限次重复博弈中，是可以实现集体利益的最优的，当然必须使δ满足相应的条件。
　　
　　三、结论
　　
　　我们分析的博弈过程都是在博弈双方都有自己和对方的完全信息的基础上的，不同的是一次博弈还是多次博弈。从上面的分析看出，相对于静态博弈和有限次的重复博弈来说，房地产开发商和施工企业之间的无限次的重复博弈无论是对于双方还是对于整个集体，都实现了较高的效率，也就是各方在追求自身的利益最优的同时，也使集体的利益达到了最优。
　　在实际中，对于双方的一次博弈，纯策略均衡（不积极施工，延期付款）是存在的。对于开发商，延期付款强化了开发商的支付控制权，而且合理地利用了资金的资金成本；对于施工企业来说，不积极施工可以降低成本，更大程度的获得利润，从而产生了道德风险。
　　所以，看待双方的关系应该从长期来看，也就是双方必须考虑各自长期的利益最大程度的优化，那么，无限次的重复博弈可以实现这样的结果。
　　同时，工程款问题的解决思路不仅可以通过上述两方之间的博弈来解决，而且可以介入第三方的力量，通过改变双方的支付矩阵，使均衡发生改变。如建立健全社会体系、积极推行工程款支付担保制度等。
　　
　　【】
　　[1] Mary Ann Dimand and Robert W．Dimand A History of Game Theory[M]．London and New york．1996。
　　[2] 谢识予：博弈论[M]．上海：复旦大学出版社，1997。
　　[3] 张维迎：博弈论和信息经济学[M] ．上海：三联书社，1996。
　　[4] 李建伟等：博弈论在房地产企业中的应用[J]．安徽建筑，2006。