摘  要  本文提出一种验证功能完善、安全性更高的门限RSA签名方案。该门限签名方案利用有理数域上的插值公式，Shamir秘密共享方案以及改进的门限RSA签名方案等理论，解决了在 中对元素求逆和代数结构扩张的问题以及共享服务器合谋的问题。     关键词  门限密码体制，门限签名，RSA算法，门限RSA签名方案 

1  引言

    门限签名是门限密码学的主要研究内容之一，最初由Desmedt和Frankel等人引进的，并基于ElGamal密码方案建立了第一个(t，n)门限密码体制。在(t，n)门限签名方案中，n个成员共享群体的签名密钥，使得任何不少于t个成员的子集可以代表群体产生签名，而任何少于t个成员的子集则不能产生签名。门限签名方案的基本假设是：在系统生命周期中，至少有(t-1)个非诚实成员。由于RSA算法满足构成门限密码体制的同态性要求，并且在CA中被广泛使用，所以这里选择基于RSA的门限签名方案。    但是对于RSA密码系统，情况要复杂一些。首先剩余环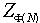不是域，其中的元素未必都可逆，于是不能利用一般的秘密共享方法共享签名密钥d；其次，为了保护RSA模数N的因子分解，不能让参与签名的成员知道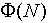，因此给在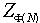上建立秘密共享方案和建立门限签名方案都带来了困难。另外一个需要解决的问题是由于采用Shamir秘密共享方案共享签名私钥，任意t个或更多个成员共享的密钥就是签名私钥，所以他们合谋可以恢复出秘密密钥，从而假冒系统生成有效的群签名。这些问题都是我们在设计门限签名方案时应该考虑的。    本文以基于有理数域上插值公式的Shamir的秘密共享方案为基础，将改进的门限RSA签名体制、两方共享与(t，n)门限方案相结合，提出了一个需要可信任中心的安全性增强的基于门限RSA签名方案。利用由hash函数建立的特殊形式的RSA签名体制，很好解决了在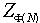中对元素求逆和代数结构扩张的问题，为实现带来了方便。同时在签名过程中对分发的子密钥、部分签名以及签名都进行了验证，保证子密钥和签名的正确性；保证在签名过程中不会被敌人入侵和欺诈，同时也防止了共享服务器合谋的危险。因此是一个安全性更高的门限签名方案。

2  门限秘密共享方案分析

    通过前面的分析我们知道门限秘密共享方案是构成门限签名方案的基础。现有的许多门限签名方案采用的是ITTC项目中的方案，采用随机和的拆分方法，也就是将秘密密钥d按多种(t，t)共享方案分割，每种分割称为一种联合，每种联合含有t份子密钥，这t份子密钥分别存储在n个服务器中的t个不同共享服务器上，不同的子密钥联合对应不同的t个共享服务器组合。这种方案具有方法简单，运算效率高的特点，但是它的子密钥分发和管理都比较困难。它需要客户机或是组合者指定共享服务器而不具有任意性，对于客户机的要求很高，实现起来比较困难。    本文采用有理数域上的插值公式和经典的Shamir(t，n)秘密共享方案作为构造门限签名方案的理论基础。这是因为Shamir门限体制具有以下特点：    (1)增加新的子密钥不用改变已有的子密钥。在参与者P₁， P₂， …， P_n中成员总数不超过q的条件下可以增加新的成员而不用重新撤销以前分发的子密钥。当系统需要增加共享服务器时，我们只需要对新增加的服务器分发新的子密钥，而不需要将已经分发的子密钥一起替换掉，这样可以减少系统的工作，提高系统效率。    (2)可以通过选用常数项不变的另一（t-1）次新的多项式，将某个成员的子密钥作废。当某个共享服务器被攻破时，需要作废它的子密钥，我们可以采用这种方法。    (3)组合者可以任意选择共享服务器的子密钥进行密钥恢复而不需要指定它们。这是我们选择Shamir(t，n)秘密共享方案的一个重要原因。当共享服务器完成部分签名后组合者Combiner可以在n个服务器中任意选择t个进行最后的组合，而不需要去指定由某些服务器的部分签名构成最后的签名。    这里我们给出这样一个假设：任意t个共享组件所构成的信息与n个共享组件所构成的信息应该是完全等价的。在此基础上给出本文的基于RSA门限签名方案。

3  基于RSA门限签名方案设计

3.1 密钥初始化

    定义5-1可信任中心A(Administrator)指将签名私钥分给n个秘密共享者的组件。可信任暗含了A一定能确保秘密信息不会被泄漏，并且在执行完密钥的分发后将签名私钥和其它信息一起销毁。    (1)假设可信任中心A选择好RSA模数N，公钥e和私钥d以及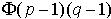，使得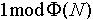。其中，模数N为两个安全大素数p，q的乘积。    (2)取定一个固定的正整数k及值域包含于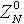(指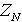中最高两个比特为0的数构成的集合)的适当的hash函数h(如MD5)，H由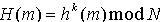得到，由于对N的分解是困难的，所以H(m)是强无碰撞的、单向的函数。    (3)d₁为随机数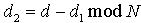，，现在可信任中心A欲将d₂分发给n个共享服务器Share Server_i 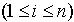，将d₁发给密钥服务器K。这里签名私钥d由d₁和d₂组成，各共享服务器共享私钥d₂。

3.2 子密钥的生成与验证

    可信任中心A按如下步骤将签名密钥d₂分发给n个共享服务器Share Server_i 。    (1)A随机选取多项式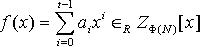使f(0)=a₀= d₂，下式：

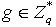    其中g是可信任中心A随机选取的信息样本。    A将d_2i秘密地发送给Share Server_i，而将N，n，e，h公开，将所有的g，c_i，y_i广播给各Share Server_i，p， q不再使用将其销毁。    (2)各共享服务器Share Server_i(i＝1，2，…，n)收到可信任中心A发送来的子密钥d_2i后，利用已广播的公开信息验证子密钥d_2i的正确性，方法如下：    ①每个共享服务器Share Server_i判断下面的式子是否成立：   

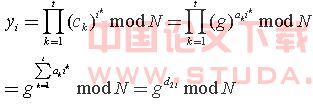    ②由于(5-4)式是所有共享服务器都收到的，因此方案中任何的组件都可以验证，故称为公开验证部分；式(5-5)由每个共享服务器自己验证，故称为秘密验证部分。对于Share Server_i来说，秘密验证就是用自己的子密钥d_2i和收到的g计算y_i并与从可信中心A发送的y_i比较是否一致来判断d_2i的正确性。    ③公开验证的正确性说明如下：    当公开验证和秘密验证中有一个不成立就认为验证失败，Share Server_i宣布可信任中心A发放的子密钥是错误的，于是可信任中心A被认为是不合格的，协议至此中止。可信任中心A将重新选择N和密钥对(d，e)重复上面的步骤发放新的密钥，否则可信任中心A分发密钥成功，可以进行下面步骤。这时可信任中心A

3.3  部分签名的生成与验证

    首先密钥服务器K利用密钥d₁对消息m的hash函数值进行签名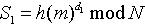。然后各共享服务器Share Server_i利用自己的子密钥d_2i对消息m的摘要进行签名，如下所示并广播其部分签名：

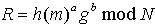    共享服务器Share Server_i生成对消息m的部分签名后，本文借助交互验证协议来验证Share Server_i的部分签名是否正确。在交互验证协议中可以由任何一方来验证部分签名的正确性，这里为了方便后面系统设计故规定共享服务器Share Server_i的部分签名是由Share Server_i＋1来验证。若协议成功，则Share Server_i＋1确信Share Server_i的部分签名S_2i是正确的；否则S_2i是不正确的。方法如下：    (1)Share Server_i＋1任意选取a，b∈_R[1，N]，计算出 并将R发送给Share Server_i；    (2)Share Server_i收到R后，计算出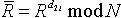并将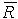发送给Share Server_i＋1；    (3)Share Server_i＋1收到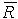后，根据下式是否成立来判断S_2i是否为Share Server_i之部分签名；    下面我们来说明协议的安全性，假设N为两个安全素数p，q之积。若非诚实验证者P不能攻破RSA系统，则上述验证RSA部分签名的交互式协议满足以下性质：    (1)完备性 若P， Share Server_i都是诚实的，则Share Server_i总是接受P的证明。    (2)合理性 非诚实证明者P使Share Server_i接受不正确部分签名的成功率是可忽略的。    (3)零知识性 非诚实验证者除了能知道部分签名是正确外，不能获得其他任何信息。因此由这样的交互式协议验证为正确的部分签名基本可以认为是正确的。

 

3.4 签名的生成与验证

    若已有t个部分签名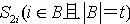通过正确性验证，则由Combiner(组合服务器)可以出共享服务器对消息m的门限RSA签名S。     (1)Combiner将x_i(i=1，2，…，t)看作整数环Z上的元素，在整数环Z上计算。

    (2)各共享服务器的门限签名S₂的计算公式如下：                    

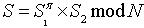最后系统的签名为。    (3)接着Combiner利用公开密钥e，按下式来验证门限签名(m， S)的正确性，若成立则接受S为m的合法签名。 

3.5 签名算法

    这里给出了门限签名方案的实现算法，其中需要运用java.io.*； java.security.*； java.math.*； javax.crypto.*； javax. crypto.spec.*；java.security.spec.*；java.security. interfaces.*； java.util.*； javax.crypto.interfaces.*等系统提供的类和方法。    (1) RSA签名私钥生成算法：      public class RSA {  KeyPairGenerator kpg=KeyPairGenerator.getInstance ("RSA")；     kpg.initialize(1024)；     KeyPair kp=kpg.genKeyPair()；     PublicKey pbkey=kp.getPublic()；     PrivateKey prkey=kp.getPrivate()；     //保存RSA公钥       FileOutputStream f1=new FileOutputStream("skey_ RSA_pub.dat")；       ObjectOutputStream b1=new ObjectOutputStream (f1)；       b1.writeObject(pbkey)；    //保存RSA私钥       FileOutputStream f2=new FileOutputStream("skey_ RSA_priv.dat")；       ObjectOutputStream b2=new ObjectOutputStream (f2)；       b2.writeObject(prkey)；}(2)子密钥生成算法：public class shareRSA {//读取私钥d及RSA参数         FileInputStream f=new FileInputStream ("skey_ RSA_priv.dat")；                ObjectInputStream b=new ObjectInput Stream(f)；                RSAPrivateKey prk=(RSAPrivateKey) b.readObject()；                BigInteger d=prk.getPrivateExponent()；                BigInteger n=prk.getModulus()；                byte[] x=new byte[16]；                Random d1=new Random()；                d1.nextBytes(x)；                BigInteger c=new BigInteger(x)；                BigInteger m=c.mod(n)；                BigInteger d2=d.subtract(m)；                //保存秘密密钥d1                FileOutputStream f1=new FileOutput Stream("partkey1_RSA.dat")；               ObjectOutputStream b1=new ObjectOutput Stream(f1)；               b1.writeObject(d1)；                //保存秘密密钥d2                FileOutputStream f2=new FileOutput Stream ("partkey2_RSA.dat")；               ObjectOutputStream b2=new ObjectOutput Stream(f2)；               b2.writeObject(d2)；                }    然后根据实际选择的t和n值进行多项式的选择，以d₂作为多项式的a₀，计算n个子密钥分发给共享服务器。    (3)各共享服务器用子密钥进行数字签名算法：public class signature {//获取要签名的数据存放在data数组     FileInputStream f=new FileInputStream("msg.dat")；      int num=f.available()；      byte[] data=new byte[num]；      f.read(data)；      //获取私钥     FileInputStream f1=new FileInputStream("partkey2i_ RSA_priv.dat")；         ObjectInputStream b=new ObjectInputStream(f1)；         RSAPrivateKey prk=(RSAPrivateKey)b.read Object()；     //数字签名                Signature sig=Signature.getInstance("MD5WithRSA")；　　   sig.initSign(prk)；　　   sig.update(data)；　　  byte[] signature=sig.Sign()；    for(int i=0；i<data.length；i++){System.out.println(signature[i]+"，")；  }}

4  结束语

    本章给出了安全增强的基于RSA可验证门限签名方案的全过程，解决了 中对元素求逆和代数结构扩张的问题，防止了共享服务器合谋的威胁。我们可以看到它是更安全可靠的，而且原理也很简单。利用这个方案我们可以将CA签名私钥分发到各个共享服务器中，通过共享服务器对用户申请的公钥证书信息进行部分签名，然后由组合服务器得到最后的公钥证书，从而保证公钥证书的安全可靠，同时也不会使系统变得复杂而难以实现。

[1] Santis A D， Desmedt Y， Frankel Y et al. How to share a function securely. In： Proceedings of the 26th ACM Symp on Theory of Computing. IEEE， 1994. 522-533 [2]D.Boneh，M.Franklin， ”Efficient generation of shared RSA keys”，in Proceedings Crypto’97，425~439[3]Desmedt Y， Frankel Y. Threshold cryptosystems. In： Brassard G ed. Advances in Cryptology——CRYPTO'89 Proceedings. Lecture Notes in Computer Science 435. Berlin： Springer Verlag， 1990. 307~315[4]N.Alon，Z.Galil and M.Yung，”Dynamic-resharing verfiable secret sharing”， ESA 1995[5]T.P.Pedersen. Distributed provers with applications to undeniable signatures.In D.Davies editor，Proceedings of Eurocryp’91，Lecture in Computer Science No.547，pages 522~526，Springer-Verlag，1991.[6]Gennaro R， Jarecki S， Krawczyk H et al. Robust and efficient sharing of RSA functions. In： Koblitz N ed. Advances in Cryptology——CRYPTO'96 Proceedings. Lecture Notes in Computer Science 1109.　Berlin： Springer Verlag， 1996，157~172[7]Boyd C. Digital Multisignatures. In H. Beker and F. Riper， editors， Cryptography and coding， clarendon press，1989，241~246