摘  要  准确的预测是帮助管理层做出正确明智决策的前提。本文首次将数据处理组合方法（GMDH）用于电信行业的数据预测，并收到良好的效果。     关键词  GMDH；预测；电信 

0  引言

    我国电信市场竞争日趋激烈，要在竞争中保持自身持续稳定，必须有针对性的制定正确及时的决策。现在各行业中广泛应用的决策支持系统（DSS）正是充分利用数据资源，进行智能化分析，从而帮助管理层做出科学决策的有效方法和手段。然而目前在实施基于数据仓库的电信决策支持方案时，往往只是构造了决策支持的基础，即仅仅实现数据仓库和多维分析OLAP，而对于如何从大量数据中提取所需信息——数据挖掘，还在进一步研究和探索中。数据挖掘是DSS中至关重要的技术，主要是发掘隐藏在数据背后潜在有用的信息，使分析者得到启示，从而真正实现决策的支持。其中，预测又是数据挖掘的重要部分，没有科学的预测就没有科学的决策，准确的预测是做出正确决策的依据。^[1]    电信行业的业务量、收入总量等指标值，往往会受到各种不同因素的影响，既呈现一定，又有一定随机性。本文首次尝试将A.G.Ivakhnenko提出的数据处理组合方法（Group Method of Data Handling，简称GMDH）用于电信行业复杂时间序列的预测，该方法用多项式作为数据处理和建模的基本形式，并在结构上有自组织和全局选优的特性，非常适合进行非线性数据的拟合。表明其预测效果令人满意，比目前广泛使用的挖掘工具IBM Intelligent Miner要好。

1  GMDH基本原理及算法

1.1  GMDH基本原理

    预测来自于对以往数据轨迹的把握，不同的预测器是以不同的方式获取数据的规律，并以此来推测未来的数据走向，原则上任何一种轨迹都可以由Kolmogorov—Gavbor多项式来表示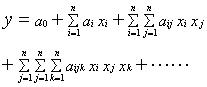：     （1）    只要有足够的数据和计算量，就可以拟合式（1）的系数，得到轨迹的表达式。然而，要完全确定a_0，a_i……等参数值是不现实的，因为随着次数和变量个数的增加，其项数急剧增加，会产生巨大的维数灾难，加之计算时的不稳定性，因而无法直接拟合式（1）建模。    70年代前后由苏联学者Ivakhnenko提出的数据处理组合方法（GMDH）通过多层自组织结构方式，解决了这一问题。    GMDH方法的基本思想是以生物有机体演化的方法构造数学模型 。由系统各输入单元交叉组合产生一系列的活动神经元，其中每一神经元都具有选择最优传递函数的功能，再从已产生的一代神经元选择若干与目标变量最为接近的神经元，被选出的神经元强强结合再次产生新的神经元，重复这样一个优势遗传，竞争生存和进化的过程，直至新产生的一代神经元都不比上一代更加优秀，于是最优模型被选出。^[2]

1.2  GMDH方法概述

    GMDH 方法只利用输入和输出变量的观测数据，不需要事先设置任何参数和模型的具体形式，而是根据研究对象的具体情况，通过计算由某些判据自动地寻找出数据间的函数关系。^[3]这种基于变量自组织和优选法原理对时间序列进行建模和预测，往往能得到满意的结果。首先从输入变量x₁，x₂，…x_m出发，对输入的每一对x_i和x_j及输出变量y计算如下的回归方程： y=A+Bx_i+Cx_j+Dx_i²+Ex_j²+Fx_ix_j      （2）    这将产生出m(m-1)/2个较高阶变量，替代最初的m个变量x₁，x₂，…x_m，对输出变量y进行估计。在从一组输入、输出观测中找到这些回归方程后，利用一个判据来对每个回归方程进行评估，选出其中最优者保留下来，得到一组（假定m₁个）对y进行最佳估计的二次回归方程（每个估计只依赖于两个自变量），再利用每一个刚得到的回归方程生成第二代输入变量的观测值，代替原始的x₁，x₂，…x_m的观测值。    和上述一样，计算y对这些新的输入变量的二次回归方程，将得到新的一组m₁( m₁ -1)/2个用新的变量估计y的回归方程。选择这些变量中的最优者，用所挑出的方程生成第三代输入变量来代替第二代，并用第三代输入变量逐对组合构造二次回归方程。继续这一过程，直到回归方程开始比前一代回归方程的估计能力有所下降。在逐代构造回归方程的过程停止后，挑选出最后一代的二次多项式中最好的一个，然后进行反向代数替换，将得到复杂的Ivakhnenko多项式。^[4]

1.3  单变量时间序列的GMDH建模

    用GMDH进行预测前，不需要了解时间序列的一些特征，仅仅根据已知样本，通过网络自组织的形式建立网络模型。GMDH网络的构建过程主要是一个不断产生活动神经元，由外部准则对神经元进行筛选，筛选得到的神经元再结合产生下一层神经元，直至具有最佳复杂性的模型被选出的这样一个过程。GMDH模型的建立需要以下几个步骤：设有时间序列{x_i},（i=1,2,…n）    1) 数据的预处理    数据预处理的方法不一，一般包括相关分析、样本离散度分析、中心化处理等，这里采用下列方法对数据做预处理：  ，其中，x为序列的均值，x_iˊ为x_i经预处理后的值（为方便，以下预处理后的序列仍用{x_i}表示）。    2) 把样本数据分为A，B两组    将{x_i}按下列方式排成矩阵

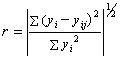     矩阵的(a)、(b)部分分别表示因变量和自变量取值，而A, B部分则分别为训练矩阵和检验矩阵，一般A组占样本总量的70~80%，B组占样本总量的20~30%左右为宜，而k的取值则根据对象的某些特性（如周期，拟周期）和经验来决定。    3）选定部分多项式，对所有变量进行两两组合    部分多项式通常采用以下形式：    y_ij=A+Bx_i+Cx_j+Dx_i²+Ex_j²+Fx_ix_j        (4)     (i≠j)    式中系数A，B，C，D，E，F由矩阵（3）中训练矩阵A估计，本文采用最小二乘法求估系数。    4）选择中间变量    用检验矩阵B数据按选定准则对（4）式得到的所有拟合方程进行评估，这里我们采用方均根判据：              （5）    其中y_ij为y_i的估计值。设定一阈值r_g，去掉那些r>r_g的拟合方程，筛选出较好的模型输出构成中间变量，作为下一层的输入，并记录该层的最小方均根r_min。    5）若该层最小方均根r_min比上一层小，则以该层模型的输出作为下一层的输入，转向步骤3)继续，否则转向步骤6)。    6）当r_min由下降变为上升时，用上一层最好的模型作为最终模型，设第k代的r_min达最小，则用第k代方均根最小的那个序列的二次函数循原路径往回代，就可得到最高阶次为2k的非线性回归模型。

2  GMDH方法用于电信数据预测

    GMDH特别适用于数据预测，目前GMDH方法已成功应用于股票市场，降雨量，天气预报等的预测。本文给出了两个用GMDH网络预测电信数据的例子。表1  某市各月份电信欠费金额（元）

年月	实际值	用GMDH计算值	用IM计算值
2000,8	3.96628E7	——	4.53419E7
2000,9	4.46599E7	——	4.76537E7
2000,10	5.46209E7	——	5.00832E7
2000,11	4.89902E7	——	5.26367E7
2000,12	6.05368E7	5.73955 E7	5.53203E7
2001,1	7.20029E7	6.56621 E7	5.81407E7
2001,2	6.84462E7	7.98948E7	6.11051E7
2001,3	6.36706E7	7.32368E7	6.42204E7
2001,4	6.08451E7	6.40432E7	6.74947E7
2001,5	6.64965E7	6.16582E7	7.09358E7
2001,6	6.58098E7	7.01210E7	7.45524E7
2001,7	7.03115E7	7.01950E7	7.83534E7
2001,8	8.04067E7	7.37680E7	8.23482E7
2001,9	8.96519E7	8.47849E7	8.65467E7
2001,10	9.53095E7	9.34776E7	9.09592E7
2001,11	1.00881E8	9.88436E7	9.55967E7
2001,12	1.07273E8	1.04933E8	1.00470E8
2002,1	1.16102E8	1.12140E8	1.05593E8
2002,2	1.17929E8	1.22060E8	1.10976E8
2002,3	1.03757E8	1.25507E8	1.16635E8
2002,4	1.10771E8	1.10749E8	1.22581E8
2002,5	1.27080E8	1.19842E8	1.28831E8
2002,6	1.33788E8	1.33149E8	1.35399E8
2002,7	1.50232E8	1.41848E8	1.42302E8
预测值：
2002,8	1.70022E8	1.64741E8	1.49558E8
2002,9	1.85796E8	1.81216E8	1.57183E8

    电信行业的业务量、收入总量等指标，往往会受到诸如优惠政策的实施、市场的波动、竞争对手的策略、节假日的安排、社会的等等各种各样因素的综合影响，既呈现一定，又有一定随机性，各数据间关系非常复杂，因而，它们所构成的时间序列可看成是一复杂时间序列。我们用GMDH方法对这类序列进行拟合预测，收到了良好效果。    表1列出了某市电信部门统计的2000年8月至2002年9月该市的实际欠费金额。我们用2000年8月到2002年7月的数据建立模型，并用所建模型对2002年8和9月欠费金额进行外推预测。选择4输入端GMDH网络，即利用前四个月数据预测后一个月数据，计算时，先将数据排列成矩阵（3）的形式，可得到20组数据样本，将前17组数据作为训练用，后3组数据作为选择评价用，最后一次迭代结束时多项式中最好的一个是  y=A+Bu+Cv+Du²+Ev²+Fuv，    式中A=32474076，B=1.25，C=-1.032，D=0，E=0，F=0。    拟合和预测的结果见表1和图1。可以看到，用GMDH方法得到的结果与实际符合得较好，尤其是2002年8月和9月的数据，既未参加训练，也未参加选择，但预测的结果却很好，预测8月份欠费额的相对误差仅为3.1%。同样这组数据，用目前广泛使用的挖掘软件IBM Intelligent Miner分析时，由表和图中可看到其拟合效果不如GMDH方法，由于样本数据并不充足，Intelligent Miner在用传统方法预测时，将模型建成一个指数方程，其整体拟合误差达到8.9%,预测8月份欠费额的相对误差为12%，预测精度远不如GMDH方法高。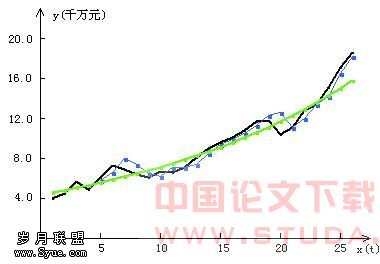图1 欠费额模型计算值与实际值对比曲线    1）实际欠费金额    2）GMDH模型的计算值    3）IM模型的计算值    因为GMDH在建立网络模型时，是通过在样本拟合精度和新数据集预测精度之间寻找平衡点，确保了即使是在小样本或数据噪声较大时，算法仍能最大程度上反映系统真实的内部关系。从而确保了所建模型的最优性和泛化能力。    图2 是分别运用GMDH方法和Intelligent Miner工具对某地区2000年6月28日到7月19日每日话务量的拟合预测结果。其数据具有一定的周期性，由图中可看到，拟合和预测的结果也令人满意。IM工具拟合的整体误差为2.8%,而GMDH方法拟合的整体误差为2.7%，其预测误差也仅为3.4%。

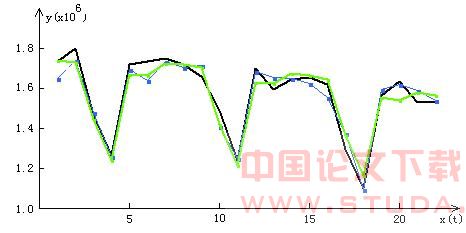
图2 某地区通话时长拟合预测结果图    1）实际通话时长    2）GMDH模型的计算值    3）IM模型的计算值    由此可见，对于电信行业中的复杂时间序列，无论是类似于图1那样无明显规律的，还是如图2的有一定周期性的，GMDH模型都能较准确的拟合数据间的关系及变化。采用GMDH方法进行建模预测，能够得到较高的精度，其准确率普遍比IM工具要高。GMDH方法完全适合于电信数据的预测分析。

3  结束语

    GMDH网络通过自组织来优化网络结构，在建模过程中需要的先验知识很少，网络的结构也可随时改变，有很高的灵活性。GMDH预测方法在建模思想和解决实际问题的能力上，都比传统的回归拟合方法要优越得多。本文针对电信领域数据特征，提出了基于数据处理组合GMDH的预测方法，计算表明，其拟合和预测的精度都令人满意，将GMDH用于电信数据的预测是可行且有效的。

[1] 孙枫林．预测技术再电信业务发展规模决策中的应用[J]．湖南大学学报，2001,（12）：117-121.[2] 刘光中，颜科琦，康银劳．基于自组织理论的GMDH神经网络算法及应用[J]．数学的实践与认识，2001，（7）：464-469.[3] 易顺民，赵文谦，蒲迅赤．河流水环境有机污染物的自组织预测模型及应用[J]．环境研究，1999,（12）：46-49.[4]  A.G.Ivakhnenko and G.A.Ivakhnenko. The review of problems solvable by algorithms of the group method of data handling. [J]Pattern Recognition and Image Analysis.Vol.5,No.4,1995,527-535