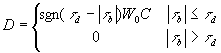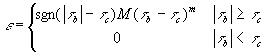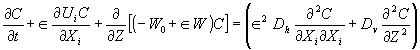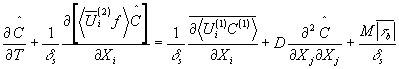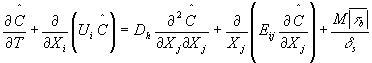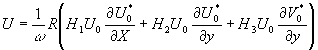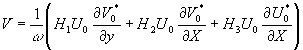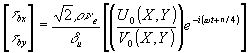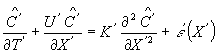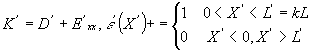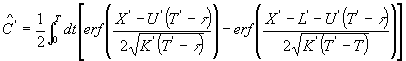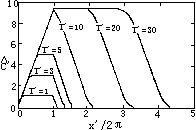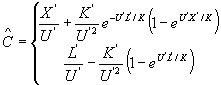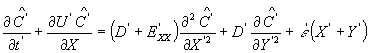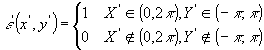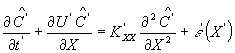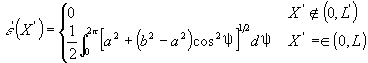波浪边界层中细颗粒粘性泥沙的再悬浮和扩散输移
摘要:本文用多尺度摄动方法从理论上推导了波浪边界层中细颗粒粘性泥沙的再悬浮和扩散输移的,并用几个算例细致地分析了波浪对细颗粒粘性泥沙再悬浮和扩散输移的作用。指出:在近岸及湖泊地区,波浪不仅是细颗粒粘性泥沙再悬浮的主要动力,而且其引起的泥沙扩散输移的强度和风生流相当。
关键词:波浪边界层 粘性泥沙 再悬浮 扩散输移
1 引言
底部泥沙的再悬浮和运移是海岸过程的中心问题。由于泥沙往往是重金属和氮、磷等污染物的载体,近年来,泥沙的扩散输移得到了广泛的研究并建立了许多数学模型。Horikawa(1968)和Van Rijn(1993)等讨论了非粘性泥沙扩散输移的数学模型[1,20],Sheng(1979,1984,1991a,b)等则建立了粘性泥沙的数学模型[12~16]。这些模型在技术和紊动模式方面比较成熟,但许多特征参数尚赖于野外和实验室资料的率定,这就增加了模型的不确定性,同时这些模型仅仅考虑到波浪对底部切应力的贡献,即对泥沙再悬浮的贡献。事实上,除了波浪对泥沙的侵蚀作用外,对悬浮泥沙的扩散输移也有重要作用。波浪二阶雷诺应力产生的波生流流速随水平方向变化,和风生流流速相当。如美国Okeechobee湖,水深较深区域的实测流速为5~10cm/s,而一波高15cm,周期3s的代表波,其一阶轨道速度为30cm/s,产生的流动大于或与风生流流速相当。同深海波生流会改变表层风生Ekman漂移(Madsen,1978)一样[4],此流动也会使近底水质点产生漂移。同时波浪边界层中较大的切应力也将加剧泥沙的扩散输移(Mei & Chian 1994)[8]。因此,一个完整的泥沙模型需同时包含波和流。为了更好地理解波浪边界层中泥沙的再悬浮和扩散输移,本文重点从理论上分析细颗粒粘性平坦海床在简谐波边界层中泥沙的再悬浮和扩散输移。
2 基本方程
对波浪边界层的紊动理论已进行了大量的研究并提出了许多半经验半理论模型和数学模型(紊动粘性,混合长度,K~ε、二阶模型等),Sleath(1990)对此进行了回顾和指出[17],不论紊动粘性系数随时间或空间变化,其给出的速度剖面与常紊动粘性系数的结果相差不大。一些实验表明(Jonsson & Carlson 1976;Horikawa,1968)紊动扩散系数随时间变化,而这种变化会对流动产生影响(Trowbridge & Madsen 1984)[1,2]。但由于实验数据太少,不足以得到可信的模式,为了得到解析解,本文采用常紊动粘性系数和常紊动扩散系数。
泥沙的扩散方程为
| (1) |
式中 C为体积含沙量,W0为泥沙沉速,Dh,Dυ分别为水平和垂直方向上的紊动扩散系数,i=1,2,(X1,X2)=(X,Y),(U1,U2)=(u,υ)分别为水平坐标及流速分量,Z和W为垂直坐标及流速分量。
对粘性细颗粒泥沙,底部边界条件为(Van Rijn,1994)
| (2) |
式中 D和ε通常有如下形式(Patheniades,1965;Krone,1962)
| (3) |
| (4) |
其中τb、τd、τc分别为底部切应力,泥沙临界淤积切应力和临界冲刷切应力,τd<τc,m和M则为系数。
在大部分河口及湖泊地区,底床表层沉积物呈半固结或非固结状态,很难承受切应力,其τd,τc非常小,伽马仪都很难测到(Patheniades,1965,Mehta & Patheniades,1982)[6,9]。本文只研究泥沙的再悬浮和扩散输移,波浪产生的底部切应力通常大于τc,因此不失一般性,本文忽略(2)中的沉积项并简化为
| (5) |
在边界层外 |
|
C=0 Z→∞ | (6) |
如果给定含沙量的初始条件,此问题变成为可冲刷边界条件下泥沙的长时间扩散问题。
3 量级分析
本问题共有三个特征长度。一是稳定含沙量区厚度δ?s,在此区域泥沙重力和垂直扩散相平衡。
δs=Dυ/ W0 | (7) |
另两个特征长度为两种边界层厚度,分别对应于动量和物质扩散。
| (8) |
其中ω波浪圆频率。 |
|
一般地,假设三个特征长度相当,也就是
O(δs)=O(δu)=O(δc) | (9) |
则Schmidt数的量级为 |
|
Sc=υe/Dv=δu/δc=O(1) | (10) |
现在我们考虑小振幅简谐波,其圆频率足够大使得
∈=KA<<1 β=Kδc | (11) |
式中K为波数,,A为近底水质点波动半径。 |
|
不失一般性,假设∈=O(β),我们可以引入如下无量纲量
Xi=KXi,Z*=Z/δc,t*=ωt | (12) |
C*=C/C0,UI*=Ui/ωA,W*=W/KδcωA |
则方程(6)保持形式不变,方程(1)成为
| (13) |
式中Pe=W0δc/Dυ是Peclet数。
在边界层中选取长度为dx的微元,微元中周期平均含沙量C的变化由水平方向上波生平流的对流和紊动扩散以及底床的冲刷决定,波生平流流速的量级为O(ωΚΑ2),则我们可得??
|
而底部切应力的量级τ0为 |
| (14) |
则可得含沙量量级C0为 |
|
| (15) |
底部边界条件(2)可无量纲化成 |
|
| (16) |
式中 |
|
| (17) |
4 扩散方程的多尺度摄动展开
通过以上量级分析,我们把量级参数放入无量纲方程(13)和(16)可得
| (18) |
| (19) |
对应垂直和水平长度尺度,此对流扩散过程有两个时间尺度。扩散穿越边界层的时间尺度和波周期相当为O(ω-1)=O(δ2/Dυ),而扩散波长的距离的时间尺度为O(1/K2Dh)这两个时间尺度的比为O(K2δ2(Dh/Dυ))≡O(β2)。考虑到假设∈=O(β),本文引进两种时间坐标t和T=∈2t,则速度和含沙量可摄动展开为
Ui=U(1)i+∈U(2)i+O(∈2) | (20) |
W=W(1)+∈W(2)+O(∈3) | (21) |
C=C(0)+∈C(1)+∈2C(2)+O(∈3) | (22) |
式中 U(n)和W(n)为Xi、Z和t的函数,而C(n)=C(n)(Xi,Z,t,T)。参照Mei和Chian(1994)的工作,我们可推得边界层上(垂线平均含沙量)的控制方程
| (23) |
式中〈f〉为f(z)沿边界层的垂向积分。
这是Mei和Chian(1994)工作的推广,其差别在于Mei和Chian未考虑泥沙的再悬浮,即没有方程(23)右边的代表底床侵蚀的源项。同样的方程也曾用在定常河流的冲蚀中(Van Rijn,1994)[8]。0
上式中![]() 产生的对流并产生明显的扩散,这类似于泰勒扩散,第二项则由紊动产生(Mei & Chain,1994)[8]。设边界层外理想流的首阶流速为
产生的对流并产生明显的扩散,这类似于泰勒扩散,第二项则由紊动产生(Mei & Chain,1994)[8]。设边界层外理想流的首阶流速为
Ui=R(V0ie-iωt) | (24) |
式中U0i=U0i(Xj),则方程(23)可化为 |
|
| (25) |
| (26) |
| (27) |
| (28) |
式中U和V为欧拉流的垂向加权平均,向量Eij由〈U(1)iC(1)〉得到,系数Hn(n=1,2,3,4)为Pe和Se的系数,Mei & Chian(1994)曾给出其详细形式和图[8]。由于H4为复数,则Eij非对称,也就是Eij≠Eji。式(25)右边的源项为一个波周期内的平均侵蚀速率,可以由底部切应力求出
| (29) |
下面我们用几个算例研究不同波型和可侵蚀底床几何条件的影响。在所有算例中Dh=Dυ=Ue=D,Pe=1,Sc=1,δs=δc=δu=δ0。由Mei & Chian(1994)可知[8]
H1=-0.122058+0.659452I | (30) |
H2=0.033333 | |
H3=-0.155391+0.659452I | |
H4=0.023615+0.233866I | |
5 前进波作用下泥沙的再悬浮和输移
设底床仅0<X<L,-∞<y<∞可冲刷,一波列垂直此可冲刷无穷条带行进,近底理想流为
U(1)=RU0(x)e-iωt=R(Ubeikxe-iωt) | (31) |
Ub=Aω=A0ω/sinhkh | (32) |
式中A0为表面波波高。底部切应力为
τb=( | (33) |
时间平均的侵蚀速率为 |
|
M|τb|=22 | (34) |
引入无量纲量 |
|
X′=kx,T′=[(k2U2b)/ω]T, U′0=U0/Ub, | (35) |
其中 |
|
C0=2 | (36) |
无量纲系数为 |
|
U′=Uω/kU2b=I(H1),D′=Dω/U2b,E′xx=ExxωU2b=R(H4) | (37) |
可得 |
|
| (38) |
其中 |
|
| (39) |
此问题的解析解为 |
|
| (40) | |||
| ||||
图1为U′=0.659452,E′=0.023615,D′=0.001,L′=2π时的解析解。初始,底部含沙浓度仅在可冲刷条带上方增加,其后部向前传递,而前部则向波前进方向延展,较长时间以后,在可冲刷区域上形成稳定的含沙浓度。
| 0<X’<L | (41) |
X’>L’ | (42) |
在此算例中K′/U′2=0.0566《1,因此稳定的含沙量主要由上式第一项决定。当含沙水体前部进入非可冲刷区域,稳定的含沙量也随之进入此区域。当然这只能在可冲刷区域无限可供沙和波浪不衰减这种理想情况下才有可能。
如果可冲刷区域为0<X′<2π,-π<Y′<π,则控制方程为
| (43) |
其中 |
|
| (44) |
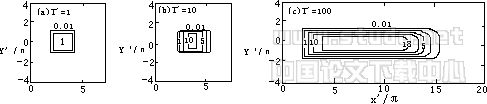
此方程可用解析或有限差分法求解。图2为含沙量随时间的变化。含沙水体先从可冲刷区域产生,逐渐成长为一圆角的矩形平台,平台前部随时间沿波传播方向延展,后部同样向前传递。由于紊动粘性较小,横向运移非常缓慢。较长时间后,在平台的后部达到一有限的高度。
|
图2 前进波作用下泥沙再悬浮和输移 |
Sediment resuspension and transportation under the actions of progressive waves |
6 垂直海墙前入射波浪作用下的泥沙再悬浮和扩散输移
设y轴和垂直海墙一致。一列单射波向海墙入射并产生反射,则表面水质点位移为
ξ=2A0cos(kx cosθ)e(ikysinθ-ωt) | (45) |
近底理想流流速为
U0=2iUbcosθsin(kx cosθ)eiky sinθ | (46) |
V0=2Ubsinθ cos(kx cosθ)eiky sinθ | (47) |
同样地用式(37)无量纲化,则扩散方程中的无量纲系数为(Mei and Chian,1994)[8]
U′=[2R(H1)cos3θ+R(H3)-R(H2)sinθ sin(2θ)]sin(2x′cosθ) | (48) |
Exx=4R(H4)cos2θsin2(X′cosθ) | (49) |
而冲刷项变为
| (50) |
其中 |
|
a=cosθ sin(x′cosθ), b=sinθ cos(x′cosθ) | (51) |
| (52) |
由于输运方程中所有系数和强制项都与Y无关, ![]() ^C′的控制方程可简化为一维
^C′的控制方程可简化为一维
| (53) |
其中 |
|
| (54) |
| (55) |
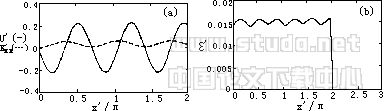
由(48)和(49)可知U′和K′xx为X′的周期函数,图3(a)为θ=π/4的U′和K′XX。从图3(a)可
|
图3 垂直海墙入射波作用下的侵蚀速率 |
Erosion rate of waves reflected from a seawall |
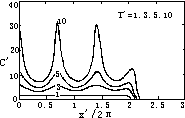
|
图4 垂直海墙入射波作用下的泥沙再悬浮和输移 |
Sediment resuspension ondtransportation of waves reflected from a seawall |
知,对流项的零点和扩散项的最小值相应,从而泥沙向直线2X′cosθ=nπ汇集,在此处扩散最弱。图3(b)为正则侵蚀速率,图4为可冲刷区域为0<X′<4π时的含沙量分布随时间的变化。明显地,泥沙趋向于向对流速度转向处汇集。
7 结语
本文从理论上论证了波浪对泥沙再悬浮和扩散输移的作用,并通过几个算例进行了详细阐述。由于波生流的强度与风生流相当,因此今后工作中应不仅仅考虑波浪对底切力和冲刷速度的贡献。
1 Horikawa.K.& A.Watanabe.(1968).Laboratory study on oscillatory boundary layer flow.Coatal Eng.Japan,11,13-28.
2 Jonsson,I.G.& Carlson,N.A.(1976)Experimental and theoretical investigation in an oscillatory turbulent boundary layer.J.Hydrau.Res.14,45-60.
3 Krone,R.B.(1962).Flume studies of the transport of sediment in estuarial shoaling processes.Univ.Calif.Hydrau.Eng.& Sanitary Eng.Res,Lab,Berkley.110 pp.
4 Madsen,O.S,(1978) Mass transport in deep-water waves,J.Phy.Occano.8,1009-1015.
5 Mehta,A.(1984),Characterization of cohesive sediment properties and transport processes in estuaries.in Estuarine cohesive sediment dynamics(ed。)A.Mehta,Springer-verlag.290-325.
6 Mehta,A.J.& Partheniades,E,(1982).Resuspension of deposited cohesive sediment beds.Coastal Engineering.1569-1588.
7 Mei,C.C.(1989)Applied Dynamics of Ocean Surface Waves,World Scientific.
8 Mei,C.C.& China,C.M.(1994)Dispersion of small suspended particles in a wave boundary layer,J. Phy.Ocean.24,2479-2495.
9 Partheniades,E.(1965)Erosion and deposition of cohesive soils.J.Hydraulics Div.ASCE,91 HYI.105-139.
10 Partheniades,E.(1971).Erosion and deposition of cohesive materials.River Mechanics,H.W.Shen Ed.Vol.Ⅱ。Ch.25.
11 Sanford,L.P.(1994)Wave-induced resuspension of upper Chesapeake Bay muds.Estuaries,17,148-165.
12 Sheng,Y.P.(1984)Modeling bottom boundary layer and cohesive sediment dynamics in estuarine and coastal waters.in Estuarine cohesive sediment dynamics[WTBZ](ed).A.Mehta,Springer-verlag.360-400.
13 Sheng.Y.P.Eliason,D.E.Choi J.K.Chen,X.& Lee,H,K.(1991).Effect of sediment resuspension on numerical simulation of three-dimensional wind-driven circulation and sediment transport in Lake Okeechobeeduringspring 1989.University of Florida Coastal and Oceanographic Engineering Laboratory Report91-019.
14 Sheng.Y.P.& Chen,X.(1991),A three-dimensional numerical model of hydrodynamics,sediment transport and phosphorus dymamics in Lake Okeechobee:Theory,model development and documentation.University of Florida Coastal and Oceanographic Engineering Laboratory Report C91-2393.
15 Sheng,Y.P.,& Cook,V.Resuspension and vertical mixing of fine sediments in shallow water,Part B,University of Florida Coastal and Oceanographic Engineering Laboratory Report C90-020.
16 Sheng,Y.P.& Lick,W.(1979)The transport of resuspension of sediments in shallow lakes.J Geophy Res.84(No.C4),1809-1826.
17 Sleath,J.F.A.(1990).Seabed boundary layers.The Sea.Vo1.9.part B.Bernard Lemehaute and D.M.Hanes Eds.Wiley-interscience.694-727.
18 Trowbridge,J.& Madsen,O.S.(1984a).Turbulent wave boundary layers.I.Model formulation and first order solution.J.Geophys.Res.89(No.C5),7989-7997.
19 Trowbridge,J.& Madsen,O.S.(1984b).Turbulent wave boundary layers.H.Second order theory and mass transport.J.Geophys.Res.89(NO.C5),7999-8007.
20 Van Rijn,L.C.(1993),Principles of sediment transport in rivers,estuaries,and coastal seas,Aqua Publications.