随机利率的三因子模型及其参数估计

                         作者：侯丽英　刘振忠　董继学

　　内容摘要：本文在分析利率期限结构模型的基础上，将影响短期利率行为特征的均值回复、随机波动和跳跃因素同时考虑到利率期限结构模型的构建中，建立了三因子模型。并且对模型参数进行了有效矩估计，比较几个同类模型，结果表明三因子模型对我国国债回购利率具有较好的拟合能力。
　　关键词：随机利率 三因子模型 有效矩估计
　　
　　随机利率模型概述
　　
　　利率作为市场上最重要的价格变量之一，一直是金融学研究的重点，特别是短期利率，它直接影响着资产定价、金融产品设计、保值和风险管理、套利以及投机等金融活动。因此，学者们提出了许多利率期限结构模型来刻画利率的随机行为，例如，Merton(1973)、Vasicek(1977)、Cox(1985)、CKLS(1992)模型等，这些模型假设利率的动态变化都遵循扩散过程，即瞬时利率可用下列随机微分方程的一般形式来表达：
　　
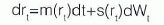
　　其中，m(rt)为漂移项，表示利率变化的瞬时期望；s(rt)为扩散项；s2(rt)为利率变化的瞬时方差；dWt为布朗运动的微分增量。当漂移项或波动率函数选择不同形式时，就能得到已有的各个著名随机利率模型，它们都属于单因子利率参数模型。
　　但金融市场自身的复杂性决定了仅仅用单因子模型来描述是不完全的，国内外大部分的实证研究表明，瞬时利率变动的总体方差绝大部分来自于两到三个因素的贡献，并且三个主要因素基本上能解释短期利率曲线80%以上的动态特征。因此本文将影响短期利率行为特征的均值回复、随机波动和跳跃因素同时考虑到利率期限结构模型的构建中，建立了三因子模型；并利用上海证交所国债回购利率数据，对模型参数进行了有效矩估计，比较已有的同类模型，说明该模型具有较好的拟合能力。
　　
　　三因子模型的建立
　　
　　在已有的期限结构模型中，CKLS模型对短期利率的动态行为特点的研究具有推动作用，现今几乎所有与期限结构相关的实证大都基于CKLS 模型或与其有关，其具体形式为：
　　drt=(α+βrt)dt+σrtγdWt（1）
　　式中，(α+βrt)dt为漂移项，α为短期利率的长期均值水平。σrtγdWt为扩散项，σ为短期利率标准差；γ表示利率波动性对利率水平敏感程度的参数，γ越大，短期利率方差对利率水平效应越敏感；dWt为标准维纳过程。对（1）中的四个参数α、β、σ、γ作适当的限制，就可得到现有中几乎所有的单因素利率模型，这些模型总体上漂移项是线性的。
　　Ait-Sahalia（1996）使用非参数方法估计短期利率的边际密度函数时，发现利率过程的漂移项和扩散项都呈现出非线性特征，即倒数形式；而AG模型则假定漂移项是瞬时利率rt的二次函数。综合以上结果，本文假定瞬时利率服从以下随机微分方程：
　
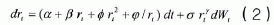
　　其中，α、β、φ、、σ、γ为常数。
　　利率的水平因素并不能完全描述利率的随机行为，波动项也表现出明显的随机特征，所以在波动项增加一个不确定因素，就能够更好地描述利率随机行为，于是基于（2）的连续时间随机波动模型为：
　
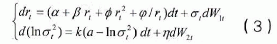
　　其中dW1t、dW2t为不相关的标准维纳过程，k为波动率因素的均值回复速度，a为波动率因素的长期平均，η为波动率因素的标准差。
　　更进一步，无论是CKLS模型还是非线性的随机波动模型，它们都是建立在随机贴现因子及其状态变量的影响因子服从布朗运动的条件之上的。布朗运动的样本路径是连续的，这意味着用布朗运动描述的变量的变化过程是连续且密集发生的，不会有跳跃或不连续的情况。
　　但从金融市场的来看，利率、股价等变量的连续性经常会被一些不可预测的随机事件所破坏，带来因子的突然跳跃，例如金融危机、股市崩盘等。为了在模型中充分反映这些突发事件的影响，本文把价格过程分解成连续和跳跃两部分，连续部分用布朗运动来描述，跳跃过程用泊松过程来描述，并且假定跳跃过程与连续过程是相互独立的，具体模型为：
　
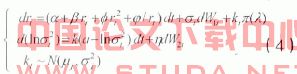
　　其中，π(λ)是产生跳跃的泊松过程，kt表示t时刻随机跳跃的大小，它是一个随机变量，服从正态分布N(μj，σj2)，称之为三因子模型。
　　
　　有效矩估计 　　
　　有效矩估计（EMM）方法是由Gallant and Tauchen提出来的，是一种路径模拟方法。该方法对随机变量的条件分布密度函数不作假定，这对利率模型的实证研究是非常理想的，因为很多连续时间利率模型的条件密度函数无法通过解析的形式表达出来。EMM方法估计的具体步骤为：
　　第一步，选择一个辅助模型并得到该模型参数的极大似然估计值，所选的辅助模型应能够捕捉到样本数据的主要结构特征，并且是一种简约形式。
　　第二步，由极大似然估计参数产生模拟数据，以辅助模型刻度向量为矩条件进行模拟矩估计，即通过最小化二次型求得结构模型参数。
　　（一）辅助模型选择
　　为了便于估计，使用连续模型的近似欧拉离散形式，设从t到t+1所用时间为1，因此（4）的离散形式为：
　　
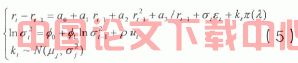
　　其中εt，ut为不相关的标准维纳过程，参数向量。辅助模型的选择首先必须能捕捉到时间序列的主要特征，并能够应用最大似然方法对模型参数进行估计。本文把观测数据映射成下列辅助模型：
　  
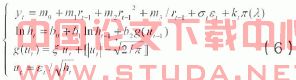
　　其中ht=E[εt2]，参数向量为θ=(m0，m1，m2，m3，b0，b1，b2，ξ，μj，σj，λ)。设转移密度为，且Yt-1=(yt-1，K，y1)，用极大似然法估计辅助模型的参数向量θ，则估计量满足下列一阶条件：

 
　　（二）权重矩阵的确定
　　对样本辅助模型的刻度向量非对称协方差的一致性估计量，若辅助模型足够近似原模型，则权重矩阵的计算式为：

　　
　　
　　实证结果分析
　　
　　（一）初始数据估计
　　尽管我国的主要存贷款利率并未实现市场化，但某些利率如CHIBOR、国债回购利率已经基本市场化。随着交易量的不断增加，这些利率在一定程度上反映了我国金融市场上的资金供求情况。

　　本文采用上海证券交易所国债回购利率R007作为无风险短期利率的替代样本，数据选择从1999-12-20到2007-12-20的每日交易收盘价。在利率模型中，各种不同期限的利率以连续复利形式表示，所以按下列公式将国债回购利率转换为等价连续复利。

    
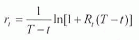
　　其中t为当前时刻，T为到期时刻，Rt为对应单利率，rt为对应连续年复利。对转化后的样本数据进行统计检验（结果见表1）。

      
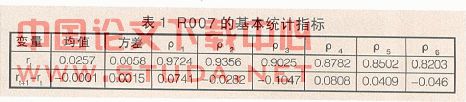
　　表1列出了rt和rt+1-rt的均值、标准差和自相关系数，其中ρj为第j阶的自相关系数。为了检测样本序列的平稳性，分别对rt和rt+1-rt进行ADF检验（结果见表2）。 

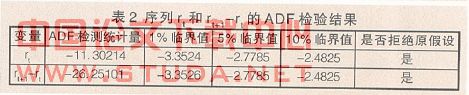
 　　从表2可以看出，rt和rt+1-rt检验的t统计量分别小于显著性水平1%的临界值，所以检验结果拒绝原假设，即可以认为序列{rt}和{rt+1-rt}在1%的显著水平下都不存在单位根，是平稳序列。
　　（二）有效矩估计结果
　　按照有效矩估计的步骤，首先对辅助模型进行参数估计，其次利用（7）式协方差矩阵，用辅助模型参数产生模拟序列，以辅助模型刻度向量为矩条件进行模拟矩估计（估计结果见表3）。

  
　　表3中td为t分布函数值，各参数值均显著，这说明上海证券交易所国债回购利率基本可以用三因子模型来描述，并且回购利率表现出均值回复特性和明显的异方差效应，不但具有时变特征，而且具有持续性。
　　（三）拟合能力比较
　　各模型能否有效地描述回购市场利率行为，主要包括两方面的比较，一是对利率水平的解释能力；二是对利率波动的解释能力。本文利用有效矩估计方法，采用相同的数据分别对几何布朗运动（GB）模型、带跳跃的几何布朗运动（GBJD）模型、CKLS模型分别进行参数估计，并在样本内条件下计算各模型的均方误差（MSE）和平均误差（MAE），作为各模型拟合能力比较标准（结果见表4）。

      
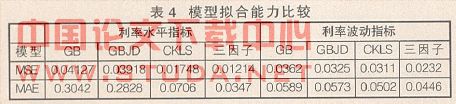
　　比较表4中的各个指标值可以发现，GB和GBJD两个模型对利率水平解释能力大致相同，变化不是很大；CKLS和三因子模型在对利率水平和波动的解释能力上虽然变化不明显，但却表现出比前两个模型明显的优势，三因子模型相对具有更好的拟合解释能力。
　　
　　结论
　　
　　本文将影响短期利率行为特征的均值回复、随机波动和跳跃因素同时考虑到利率期限结构模型的构建中，建立了三因子模型，它不仅能够嵌套漂移项为线性和非线性的两类模型， 并且在非线性的形式上包括了二次函数和倒数函数形式。通过对我国货币市场的利率进行参数估计和结果的比较，表明随机利率的三因子模型能够较好地描述我国货币市场利率的非线性均值回复和异方差特性，从而为利率相关的问题研究奠定了基础；另外模型的参数估计部分运用了有效矩估计方法，解决了传统最大似然估计法需要显式条件密度函数的难题，也避免了广义矩估计对小样本特性数据估计不完整的缺陷，该方法在期限结构模型的实证估计中具有较好的应用前景。
　　
　　：
　　1. Duffie D, Singleton KJ．Simulated moments estimation of Markov models of assets prices[J]．Econometrica , 1993 , 61
　　2.Gallant A R, George T．Estimation of continuous time models for stock returns and interest rates[J]．Macroeconomic Dynamics , 1997(1)
　　3.Chan K C, Karolyi A, Longstaff F, et al．An empirical comparison of alternative models of the short-term interest rate[J]．Journal of Finance , 1992 , 47 (3)
　　4.周丽，李金林，冉伦.随机波动利率期限结构的有效矩估计[J].北京理工大学学报，2006（5）
　　5.马晓兰，潘冠中.单因子利率期限结构模型的广义矩估计及对货币市场的实证检验[J].数量技术经济研究，2006（1）