“第三次世界大战”的预言——金融“核”战争
人类正经历着从“野蛮”残杀转变为“文明”博弈时代的蜕变,但人的本性并没有改变,只不过是随着时间的其表现形式呈现为螺旋式推进。
在完全市场体系下,投机且唯有投机是遏制与化解人类这一“战争”危机的有效途径。其效果看起来就像人类正因为核武器的发明,以毁灭性的武器,最终达到了避免大残杀的效果。在混沌的世界里,人类的一切多么像自组织临界点的舞蹈!
摘 要:金融安全关系到国家经济发展、社会稳定、国防巩固,是国家安全的重要组成内容。在当前国际经济、金融一体化发展趋势中,金融交易市场安全的重要性尤为突出。特别是不断出现的金融风暴的影响和日益显著的金融交易市场波动的全球化趋势已使预测并控制大的金融风险成为各国政府和金融机构严重关注的问题,并且这个问题正在变得日益严峻。
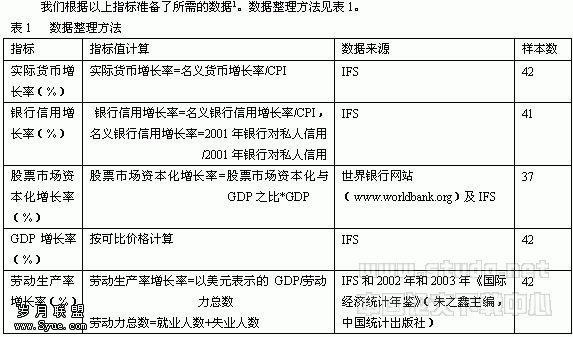
目前,金融市场交易系统提供的各种高频数据与物研究体系在时空结构上具有相当程度的严格对称性,可反应出系统的演化过程和行为特征,并且数值模拟技术已经为金融市场数值预测研究提供了前所未有的技术基础,因此现在已经进入了探索和构造金融市场物理模型并用高频金融数据检验这些模型的模式辩识与市场演化趋势跟踪能力的时代。
尽管金融交易市场价格波动预测是一个举世公认的国际性难题,但在强化各种减轻金融交易市场风险问题措施的同时,仍须大力推进金融交易市场数值预测研究。为此,需要打破长期徘徊在以线性的、完全理性的均衡范式的(主流)金融学为基础的经验性预测局面,把注意力尽快转向研究以非线性动力学为基础的金融交易市场价格波动数值预测。
以金融交易市场数值预测为目标的非线性金融市场动力学的理论、模拟试验和实际观测,数据同化和软件的开发应成为今后研究的重点。现在的问题是,需要我们积极借助数值分析天气预报、物理建模地震预测和航位推算弹道导弹等学科领域的经验,强化多学科,多部门的组织协调,尽早在我国股市和期市开展金融交易市场价格波动动力学数值预测的科学试验。金融交易市场价格波动数值预测研究必将极大地促进我国金融市场基础研究和金融风险预警系统的进一步发展。
关键词:国家安全,金融安全,金融市场,价格波动,数据挖掘,数值预测
一、问题的提出
金融之威力可以从亚洲金融风暴看得很清楚。原本经济很有活力的东南亚,1997年的10月一夜之间数百亿美元被调得无影无踪,致使东南亚的经济陷于瘫痪,元气大伤。
由于近年来发生在全球一系列灾难性金融风暴预先没有察觉,引发了国际金融科学界关于“金融市场能否预测”,“是否应该把金融市场预测作为研究目标”的激烈争论。值得指出的是,我国学术界对如何推进金融市场预测研究尚无具体、明确的认识,甚至对是否应该把发展的重点放在金融市场预测也有不同的看法。
随着加入世贸组织过渡期的结束,随着国民待遇的实现,市场准入的逐步放松,金融业面临的国际竞争将进一步加大。这要求我国尽快建立全方位、多层次的金融市场体系。其中防御和减轻金融市场风险对我国来说是一个无法回避的重要问题。其发展战略和技术路线不但是专业部门的问题,同时也需要引起相关部门和相关学术领域的关注。这是因为金融市场孕育、发生的过程确实十分复杂。突破金融市场预测难关不但涉及若干金融学分支;甚至远超出金融学的范畴。开放的,而不是封闭或半封闭的研究和探讨,无论从那个角度来说都是绝对必要的。
近年来,金融学的基础研究得到了较大的关注,尽管多数研究给人以鞭长莫及的印象,但在金融市场数值预测方面已经有了实质性的突破。今后的发展方向和发展战略问题已经到了必须进一步深思和研讨的时候。为此,本文试图对今后我国金融交易市场价格波动数值预测(简称金融市场预测)研究的发展问题提出某些未必成熟的思考和建议,希望有助于打破某些固定的思维模式,有助于吸引其他部门领域的关注,有助于推进我国金融市场预测事业的发展。我们的讨论将从最基本的问题开始。
二、金融市场预测研究面临的社会需求和压力
当前,世界金融市场的表现与发展具有经济与、金融与贸易、投资与投机交错和复杂性扩大的特点与趋势。世界金融市场的研究特点和趋势是,在方法论方面,从原来线性的、完全理性的均衡范式、使用传统的统计学方法(主流金融学)向非线性[1]-[4]、有限理性的非均衡范式、应用分形维数理金融学方法(基于复杂系统理论的金融经济学,如金融物理学[5]、信息经济学和行为金融学[6])转变;在空间方面,将市场宏观层面的研究与微观结构的研究结合起来向市场生态系统[7](有机整体)的研究拓展;在技术手段方面,计算机技术的发展促进了实验金融学的产生和发展,目前能够获取的金融和经济的高频数据如同物理实验一样,提供了验证或推翻任何相关理论的手段。总的发展趋势是,将现代数理金融学[8]从现有架构基础上提升到分形维尺度的复杂系统层面。
当前,中国金融交易市场(股票、期货)日趋成熟,总体而言,进入到了一个“协同博弈”阶段。由于金融交易市场是一个非均衡的演化着的复杂系统,因此,股市和期市的交易价格波动显然是一个非线性动力学[9]问题。由此可知,对于这样一个混沌的金融市场,应用均衡范式的主流金融学方法,以及仅凭经验地、直觉地进行金融市场预测显然是不科学的,存在着很大的问题,其盲目性,不确定性因素太大,难以真正认识和发现金融交易市场价格波动的。而科学有效的方式方法是,基于复杂系统科学理论,以非线性动力学建模,可以面对更为多样且更真实的金融交易市场情况,是解决金融交易市场复杂问题和进行金融交易市场预测的有效途径和手段。
从复杂系统理论角度研究现代金融市场,一些学者进行了市场混沌特性、分形、分数布朗运动等实证研究,对市场的本质有了较深刻的认识,[10]-[14]但对金融交易市场的高频数据进行数据挖掘,建立与市场相适应的前瞻性的控制模型,特别是为管理决策者提供具有实用价值的金融市场数值预测,这方面的研究工作尚未见公开报道。
随着我国金融市场进一步对外开放,金融市场将变得更加活跃和复杂。这种基本的金融市场背景决定了我国必然长期面对大范围金融交易市场频繁活动和价格波动暴涨暴跌频发的局面。我们必须对我国面临日益增加的金融交易市场价格波动风险(简称金融风险)威胁有足够清醒的认识。
为抵御和减轻这些金融风险,最主要的措施可归结为两个方面:一方面从金融生态环境自身建设层面上加强相关政策制度的制定和实施,搞好金融风险设防,对于减轻损失具有极为重要的作用,这并没有异议。另一方面,从科学技术层面上加强金融风险的定量预测和控制,金融市场预测最重要的价值在于提前采取必要的防范措施,这对于减轻和消除金融风险,保持社会稳定具有重要意义。随着国民经济的快速发展,金融风险问题作为各类风险的集中表现显得尤为突出和重要,因此,必须进一步加大对金融市场预测研究的投入,其中股市和期市为其预测研究的重点。这是我们无法回避的现实。三、由市场能否预测争论引发的思考
首先,让我们来从层面对“预测”(Prediction)概念进行认识,预测特指由专家做出的科学研究的并给出确定性的结论,具体是指根据对象属性之过去观察值来推估该属性未来之值,为决策问题提供定性或定量的决策信息。如地震预测,用科学方法对未来地震发生的时间、地点和强度(震级和烈度)作预先的估计。预测的准确性(精度)取决于对所预测系统的认识程度及其所采用的预测物理模型及其方法。此外,在预测时间上,按照时间尺度的长短不同,可以(人为地)分为长期预测(年时间尺度)、中期预测(月、日时间尺度)、短期预测(时、分时间尺度)等,这是一个人为的工作分类,并无明确的物理意义,并且不同作者对于这些术语的意义也有不同的理解。
金融市场是一个演化着的复杂系统,类似于地震和飓风的科学现象。各类市场参与者共同构成了开放的市场生态环境,且在混沌的市场状况下不断调整彼此关系及局部的非线性相互作用,而自发地涌现出的系统总体性状、结构与动力学行为。金融市场预测的科学前提是认识金融市场孕育和发生的生态环境演化过程,包括各类市场参与者共同构成的市场的异常变化。但是人类对金融交易市场价格波动的成因及其发生的还知之甚少,主要是因为由人所出来的金融市场行为,不同于其它属于纯物理过程的自然现象,其影响因素过于复杂,还可能有人类未知的因素存在,可以说是更高层次的自然现象。不过,从金融物角度来看,价格涨落本质应该是在某一区域的构成介质(市场参与者)的非平衡定态发生失稳,并伴随有应变能的加速释放(响应发生:价格波动、暴涨、暴跌)。[15]这与地震发生的原理十分类似。
尽管在金融市场预测的研究和实践方面开展了大量有价值的工作,但我国金融市场预测主要仍是基于线性的、理性的均衡范式的(主流)金融学系统下,人们所能做的是对一些基本面信息进行分析和观测,或者应用一些有限的手段对已发生的行情进行所谓的技术分析和观测,这种分析和观测通常是不完全的和不完善的,其认识必然都带有很强的局限性和主观性。我们不难发现,各种统计方法充斥于现有的金融市场预测。这是经验预测合乎逻辑的必然结果。统计方法虽可用于寻求宏观规律或某种因子关系,并在研究的初级阶段具有某种价值和意义,但进一步的深入则有赖于对问题本质的揭露。总体上,定性的金额市场成因研究较多,定量的金融市场动力学研究相对不足,对今后的发展缺少明确、具体的突破方向。如果不能建立金融市场预测的新理论,金融市场预测的效果和水平将会长期停滞在目前的状况,难以适应我国金融风险威胁日益增大的形势。
不可否认,金融市场预测的确是一个国际性的科学难题。正因为如此,金融学界至今对金融市场能否预测仍没有统一的认识,某些学家甚至以非常率直的语言表达了明确的否定意见。应该说这些为经院学者们所不屑的“金融市场数值预测”,的确不是传统的金融学的内容。但换个角度来看的话,又确实是金融投资市场中的一场博弈(信息经济学)。我们很遗憾地发现,长期以来学者对市场“技术分析”人士的工作内在原理(物理学、动力学)没有足够的重视,尽管价格波动问题困惑着包括学者们在内的所有人。然而,金融市场的高速发展又促使我们从理论原则的高度,重新审视价格波动预测面临的困难和问题。所幸,复杂系统理论,非线性动力学(混沌、分形、孤子)在新世纪已受到人们越来越多的关注,会不会出现金融学的新纪元?
长沙非线性特别动力工作室基于复杂系统科学,应用非线性动力学原理,进行了“金融交易市场价格波动数值预测建模”研究开发,即对现代金融交易市场数据,如价格、成交量、时间区间等,进行多种特定的相空间重构和时间序列处理;在重构的高维空间中,构造非线性特别动力因子——金融孤子;将无规则可寻的锯齿状价格波动映射成较光滑的函数曲线;运用鞅方法和不动点理论,以动力因子处理连续时间的市场价格波动(即所谓布朗运动),实现对金融交易市场价格波动进行跟踪逼近和预测。该模型具有气象预报一样的数值分析、地震预测一样的物理建模、弹道导弹一样的航位推算的特点。[16]
显然,对于如此重要、如此复杂的金融市场来说是十分需要这样数值预测的,能作出有实用价值预测,即同时报出发生时间、市场(指数或品种)和强度(幅度),且越准确越好,越早越好。但是,要达到这一点对科学家来说挑战很大,你要知道,预测未来,特别是预测比较长的未来,预见发生一个实际上概率很小的事件发生的未来,这个风险是很大的。但这并不意味着对金融市场预测的否定,而只是对金融市场预测的提法要更加科学、合理。
首先,应该认清金融市场动力学系统到底是完全混沌系统还是“弱混沌”系统,这是一个非常重要的问题。
完全混沌系统是指不稳定和无序的体系存在一个时间尺度,超过这个时间尺度,就不可能对其行为进行预测。如地球大气的时间阶段是以五天为单位的,也就是说,每五天空气在地球上流动一次。人们在五天的时间段中可以精确地推算出天气变化的情况。但是,要预测出更长时间的天气变化就需要精确地掌握当前的大气状况并要进行几乎是不可能的复杂计算。我们不可能超越季节平均值预测六个月以后的气候变化。据此,金融交易市场价格波动是不可长期确定性预测的。
弱混沌系统,即自组织临界状态的系统,不存在这样一个时间尺度,因而可以对其行为进行长期预测。[17]据此,金融交易市场价格波动是可长期确定性预测的。
不管将非线性金融市场动力系统看成完全混沌系统,还是将其看成“弱混沌”系统,确定性的短期(有限时间内)预测都是有效的,这里的预测有效不是一个精确值,而是一系列的逼近值。因为,混沌的初始条件敏感性使得对于未来的测量不存在精确的办法。长期预测成为不可能,但只要有足够好的模型和对初始条件的精确观察,它的确定性却使之在预测能力消失以前可以进行短期预测。要准确地预测金融交易市场价格波动发生应该包括四个要素(具体时间、具体指数或品种、具体价格涨落幅度以及具体成交量),显然这是不可能的事情。由此可知,对于金融交易市场价格波动发生的具体时间、波动幅度以及成交量是不能事先预测的。看来,对于金融交易市场价格波动的预测更加科学和合理的提法是趋势的跟踪逼近,类似于代数中“无穷小”概念,某些曲线可以无穷接近坐标轴,但永远不会与坐标轴重合或相交,也就是永远会有误差存在。然而,即使就是这样的跟踪逼近也是一件十分困难的事情,即金融市场的凯恩斯选美难题,这是一个世界性科学难题。
要开展金融市场预测研究工作,必须具备和完善以下条件和基础。
(1)有必要进一步深入分析不同时间尺度金融市场预测的主要难点,并应遵循先易后难的原则,确定金融市场预测的突破方向,恰如其分地确定金融市场预测的内涵和阶段性目标。如长沙非线性特别动力工作室对金融交易市场的高频数据,运用多种数理原理进行数据挖掘,得出了一些不同于主流金融学的结果,即价格波动的有限尺度布朗运动,它是指在证券期货市场中,追踪价格波动的一种操作性概念,具体来说,是根据交易市场高频数据所构造的空间时序结构,选择与其相匹配的尺度并进行划分和变换,应用分形原理发掘标准布朗运动中的关联增量过程,从而发现相应尺度的有偏随机游走的趋势(上鞅或下鞅)。
(2)必须充分重视不同时间尺度金融市场预测研究的科学基础,不能把追逐不同时间尺度的涨跌前兆指标作为发展金融市场预测的基本思路。金融市场的形成必然伴随非平衡定态的积累和失稳过程。因此,相应的动力学研究应是解决金融市场预测难题最根本的科学基础,并应作为我们集中力量研究的重点。
(3)天气变化、地震形成和金融交易市场价格波动都是自然界中的非线性复杂过程。就非线性复杂过程的预测本身来说,金融市场与地震和天气一样,应是有可能做出某种时间尺度的预测。对金融市场预测研究来说,天气预报和地震预测的经验值得借鉴。在现阶段,没有必要把金融市场形成过程中的非线性混沌现象作为金融市场预测研究的障碍,而应把研究和发展金融市场动力学预测作为今后金融市场预测发展开拓的主要方向。
四、市场数值预测的可能性
所谓数值预测指的是根据数据记录中的其他变量预测某个连续变量的值,实质上就是根据物理问题的数学模型对系统的演变过程作出定量化的结论。
金融市场数值预测包括了对金融市场具体指数或品种价格波动成因及其动力学过程的研究。金融交易市场价格波动是由影响金融市场的内部、外部等因素之间复杂的关系。外部因素有国家的政策、方针、上市公司的各种行为、产品的销售、竞争中的优劣等,内部因素是市场参与者的心理预期和操作策略等,它的变化直接产生系统的波动。即使是同一国家甚至同一地域的两个市场,都可能有明显的不同。但金融市场的某些观察量,如:交易价格、成交量、交易频率和市场指数值的统计性质对于十分不同的金融市场看起来却有令人惊讶的相似性。这意味着金融市场作为复杂动力学系统可能存在“普适”的行为与。这些都构成了进一步深入开展金融市场非线性动力学预测研究的理论和技术基础,而数值分析则是揭示金融市场的涨落规律,发现能够导致涨落和变化的因素与动力学机制以及推进金融市场动力学预测最根本的途径和手段。
与天气、地震系统一样,金融市场的孕育和形成并不是一种孤立现象,而是多种因子相互作用的结果,可视为相互作用的多粒子体系,并表现为一种复杂过程。因此,任何孤立因子的研究都不可能对金融市场的孕育和形成过程作出有效的预测。数值预测的优势恰恰在于对金融交易市场价格波动的完整过程进行系统的,而不是孤立的研究。
根据天气数值预报的经验,对某种系统演化过程进行数值预测的必要条件:(1)必须对研究的系统有较为充分的理论认识,即能够建立起充分反映问题本质的数学-物理模型;(2)必须能够对该系统进行符合客观实际的参数化;(3)必须具备相应的数据处理能力。金融市场数值预测的必要条件如下:
1.金融市场数学-物理建模
金融市场数值预测能否可行的最大疑问首先在于是否能够建立相应的物理模型和数学模型。关于金融市场与物理时空结构对称性研问题,应该说已有的研究成果已经为此提供了相当的理论和实验基础。[18]-[24]长沙非线性特别动力工作室应用金融孤子(非欧几何)构造规范变换建模。
应用非Abel定域规范变换方程
, (1)
其中, 为非线性动力特征函数, 为对数的底, 是虚数单位, 是孤子的特征量, 是描写该变换的参量。进行多种时空、规范对称变换,特别是非Abel定域规划变换,辨识孤子。[25]
价格波动的自组织临界性决定了转捩点(皮卡不动点)的存在,因此,应用不动点理论
, (2)
可以对价格的波动峰、谷值可推算逼近、辨识和确认,判别临界点(峰不动点),指导买卖交易。[26]
鞅方法为带预期的最优消费选择,运用杜布半鞅分解定理跟踪价格变化趋势
, (3)
当谷不动点测出,跟踪上升趋势时,这里 ;当峰不动点测出,跟踪下降趋势时,这里 。本实验应用上鞅方程 跟踪波动趋势。[26]
当前人类对价格波动形成过程认识的不足并不应该成为进行金融市场数值预测研究的障碍。恰恰相反,金融市场数值预测的实践将会进一步检验和有力地推进人类对金融市场复杂过程的认识,并将在很多方面弥补单纯理论研究和实证实验的不足。如长沙非线性特别动力工作室基于复杂系统,以非线性动力学原理建模,应用鞅与不动点理论对金融交易市场进行数值预测,关注动力学的时间关联和非平衡态性质,在实践中已经有了较好的结果。由此可知,进行价格波动数值模拟研究,首要的问题并非来自物理模型本身的缺陷,而常常是因为缺乏对金融市场复杂性的数据挖掘,以至于以往的动力学数值模拟研究不得不限于的或者定性的研究阶段。
2.金融市场高频数据参数化
机科技手段处理下的股票、期货等交易市场,提供了巨量的市场参与者的交易数据,高频数据这为开展金融市场复杂介质结构及其动力学响应奠定了前所未有的技术基础,并对以价格波动数值模拟为目标的模型参数化无疑具有重要意义。
金融市场的模拟离不开边界条件的确定,但边界条件的确立可以看成是一个金融交易市场价格波动数据的反演过程[27]。价格波动的连续观测提供了不断修改边界条件,并逼近真实情况的可能性。金融交易市场数据可以提供金融市场即时数据。通过相应的数据的数值模拟可以获得研究区域内价格波动过程及其能量释放的各种信息和数据,以及参与者的行动过程。因此,可以对实时交易市场的数据,如价格、成交量、时间区间等,进行多种特定的相空间重构和时间序列处理,在重构的高维空间中,构造非线性特别动力因子(金融孤子)。通过对金融交易市场数据挖掘,可以得到相关动力学的行为特征。
3.数据处理系统
实时跟踪逼近金融交易市场,包括价格波动的孕育和形成过程无疑是一项复杂和艰巨的任务。强大的数值计算能力是不可缺少的支撑条件。幸运的是,现在我国证券交易市场和期货交易市场上所使用的计算机系统已经为此提供了前所未有的技术基础,并仍有巨大的潜力。例如我国证券和期货交易所均拥有适用可靠的计算机交易系统,通过高容量光纤及数据专线、双向卫星、联网等通讯手段确保前台和远程交易的实时和安全可靠。同时,通过中心数据库实现结算、资金、交割、异地交割仓库、风险监控等系统数据的实时同步传送和交换。因此,对于金融市场数值预测来说,计算和数据处理能力应该并不存在不可逾越的技术障碍。
这实际上是长沙非线性特别动力工作室开展的,命名为金融市场数值预测计划——金融交易市场价格波动数值预测建模。该工作室的同仁们发现这些高频数据有效地描述了市场参与者的行动过程,而行为心理的原理表明,这些交易活动就是群体的高阶逻辑思考过程(信息)的反映,即发现了金融交易市场非线性特别动力因子(金融孤子)存在,并且根据孤立波是非线性方程的行波解,孤子具有粒子的特性,通过孤子可以观察跟踪一些非线性变化,从而为金融市场(股票、期货)交易价格波动行情进行跟踪、预测提供依据。该项研究的主要目标是要利用股市和期市的交易数据,研究金融市场预测的数值方法。该项研究已经完成无交互作用模拟操作实验(表1),以及股票、期货实盘交易(附件1),尽管在为管理决策者提供金融市场数值预测方面仍面临着一系列理论和技术的问题仍然需要解决,但这标志着金融市场预测研究将开拓数值分析的新纪元。如果我国的金融市场预测研究仍然固守原有的研究思路而裹足不前,那末我们将面临失掉机遇的危险。
表1 中国联通600050数值分析及交易报告
Table 1 The numerical analysis and trading report of China Unicom 600050
基本面 大盘、电信、指标股
流 动 性 评 估 1.流通盘 (总持仓量) M= 500,000 万股/仓单
2.流通市值 Q=H×M= 1,555,000 万元,今日收盘价H= 3.11 元/股
3.区间统计
类型 时间 成交万元 换手率% 振幅% 均价元
长期 021011~030918 6,724,076 425.57 35.50 3.16
中期 030319~030918 3,771,463 233.53 25.88 3.23
短期 030725~030918 287,610 17.92 7.44 3.21
价格波动模式识别 不动点类型 时 间 价格元 成交额万元 换手%
逼近 谷 (谷/峰)不动点 030912 3.17 8,976.0/日 0.56
辨识 谷 (谷/峰)不动点 030930 3.10 5,480.6/日 0.35
确认 谷 (谷/峰)不动点 031119 3.41 7,842.5/日 0.64
辨识、确认 上 (上/下)拐点 040113 4.89 90,760.5/日 3.56
波 动 曲 线 模 式 图
交易结果 买入:
共 32日 交易单位(分、时、日)
最高价 3.64 元/股,最低价 3.07 元/股,振幅 18.56 %
均价 3.37 元/股,换手率 52.12 %
总交易量 26,060万股,总交易金额 878,336 万元
总 买入 (买入/卖出)量 260,600,000 股
总发生金额 878,336,000 元 卖出总结:
共 10日 交易单位(分、时、日)
最高价 5.36 元/股,最低价 4.61 元/股,振幅16.26 %
均价 5.00 元/股,换手率 36.06 %
总交易量 180,300 万股,总交易金额 902,786 万元
总 卖出 (买入/卖出)量 260,600,000 股
总发生金额 1,303,000,000 元
结果统计 交易成本:(87,833.6+130,300)×0.8%=1745.7万元
收 益:130,300-87,833.6-1745.07=40,721.33万元
收 益 率:40,721.33÷87,833.6=46.36%
运 作 期:030930-040205共计127天。
报告人: 马非特 签收人: 马金龙
五、结论和讨论
金融市场数值预测的重要价值是不可否认的。为了解决社会发展对金融市场预测的需求与金融市场预测水平处于徘徊不前状况的矛盾,我们必须对我国金融市场预测研究发展的方向和重点作出新的战略决策。其根本出路在于必须尽快开拓以金融市场数值预测为导向的发展道路。固守经验预测的后果将严重制约金融市场数值预测研究的发展,难以改变金融市场科研与预测实践脱节的状态。
金融市场预测研究应该充分吸收和借鉴气象预报、地震预测和弹道导弹等学科领域的成功经验,谦逊地吸纳人类的最高智慧,如数学、物理理论,建立模型来指导自己的实践活动。应用非线性动力学原理充分对金融交易市场数据进行挖掘,建立的金融市场数值预测系统,随着该系统的建设,实际观测经验的积累和相关理论研究的深入,金融市场预测问题将会不断取得实质性的进展。最后,建立由金融市场系统概念的产生并形成数值模式。应该指出的是,金融市场是由这么一群人构成的一个时空世界,比起那些相对缺乏生命活力的物理世界来,自然还要复杂得多,因此,应上升到一个新的层面来对待。长沙非线性特别动力工作室的最新研究表明,现代金融市场这一战场,早已从原始的TNT“炸药”时代进入了原子“核”时代。所以,战争的成败恐怕将取决于“核”能的威力,而不是简单的炸药吨位的多少。在这个问题上必须要有清醒的认识。
鉴于金融市场数值预测的技术特点,当前金融市场数值预测突破的目标无疑应首先主要集中在金融市场的中、短期预测。根据我国的具体情况,目前在股市和期市的有关指数或品种作为研究的重点。现阶段的当务之急在于选择某些流动性好的品种作为试验对象,建立相应的研究开发组织,开展理论和方法研究,开发相应的技术软件,通过实时模拟(或实盘)同步交易操作实践,尽快取得经验和实效。
在金融市场数值预测研究的带动下,价格波动失稳的过程的阵列连续跟踪观测,金融市场的属性及性质,金融风暴的触发条件,金融市场的孕育和失稳过程的理论、模拟试验和实际操作,非线性金融市场动力学等都将成为研究的重点。在推进金融市场预测取得实质性进展的同时,这也必将有力地推动我国金融学及非线性动力学的快速发展,并在一系列关键性科学和技术问题的研究方面走向深入。
[1]欧阳莹之. 复杂系统理论[M].上海:上海科技出版社,2002,1-140.
[2]陈平. 文明分岔、混沌和演化经济动力学[M].北京:北京大学出版社,2004,4-560.
[3]宋学峰, 杨列勋, 曹庆仁主编.复杂性研究进展[M].全国第一、二届复杂性科学学术研讨会集,北京:科学出版社,2004,1-429.
[4]埃德加•E•彼得斯. 资本市场的混沌与秩序[M].王小东译,北京:经济科学出版社,1999,64~83.
[5]卡里尔•伊林斯基. 物[M].殷剑峰,李彦译.北京:机械出版社,2003,1-94,246.
[6]李心丹. 行为金融学——理论及的证据[M].上海:上海三联书店,2004,1~211.
[7]戈峰. 生态学[M].北京:科学出版社,2002,4-460.
[8]史树中. 金融经济学十讲[M].上海:上海人民出版社,2004,1-249.
[9]刘秉正,彭建华. 非线性动力学[M].北京:高等教育出版社,2004,1-565.
[10]埃德加• E•彼得斯. 分形市场分析——将混沌理论应用到投资与经济理论上[M].储海林,殷勤译,北京:经济科学出版社,2002,1-325.
[11]Peters, E. Fractal structure in the capital markets[J]. Financial Analyst J, 1989(7):434-453.
[12]G W Wornell and A V Oppenheim. Estimation of fractal signals from noisy measurements using wavelets[J]. IEEE Transactions on Signal Processing, 1992,40(3):611-623.
[13]B B Mandelbrot, H W Van Ness. Fractional Brownian motions, fractional noises and applications [J]. SIAM Rev, 1968,10(4):422-436.
[14]H E Hurst. The long term storage capacity of reservoirs [J]. Transactions of the American Society of Civil Engineer, 1951,116:770-808.
[15] 马金龙,马非特,金融市场开放交易系统的自适应控制投资模型的研究.2005,中国金融学术研究网http://www.cfrn.com.cn.
[16]孤立波、非线性动力与价格波动投机——金融市场凯恩斯“选美问题”有解可求.期货日报,2005年11月10日,第三版.
[17] Per Bak and Chao Tang. Earthquakes as a self-organized critical phenomenon[J]. Journal of GeoPhysical Research. 1989, 94(BⅡ): 15635-15637.
[18] Robert J. Aumann. Existence of competitive equilibria in markets with a continuum of traders. Econometrica.1966, 34, 1-17.
[19]Schaden M. Quantum finance[J]. Phys A. 2002, 316, 511-538;
[20]陈泽乾、汪寿阳. 量子金融的几个问题[J]. 科学进展,2004,14(7):742-748.
[21]Young K. Foreign exchange market as a lattice gauge theory[J]. Am. J. Phys. 1999, 67, 862-868.
[22]Emanuel Derman. The perception of time, risk and return during periods of speculation[J]. Quantitative Finance,2002, 2, 282-296.
[23] Shi Leilei. Does Security Transaction Volume/Price Behave a Probability Wave? [J], Physica A, (待刊).
[24]谢彦波. EZ模型中的有限尺寸效应[J]. 物理学报,2003,52(10),2399-2403.
[25]金融交易市场发现孤子存在的意义——橡胶、沪铜实时模拟同步交易实验报告.2005,中国金融学术研究网http://www.cfrn.com.cn.
[26]马非特、马金龙,基于鞅与不动点的数值预测原理——少数人博弈惯性策略.2005,价值中国http://soliton.chinavalue.net.
[27]肖庭延等. 反问题的数值解法[M].北京:科学出版社,2003,1-244.



![金融资本全球化是否历史发展的必然[下]](/d/file/20100626/b3c2c2820f9fdcfe57ba7658c0bbc299.jpg)