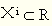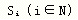经济增长和“均衡”是什么关系？

内容提要：本文首先指出“均衡”概念的局限性，认为研究增长尤其不能使用“均衡”概念。经济学家必须首先弄清楚自己是在研究什么经济问题，然后才考虑使用合适的数学方法。文章最后期望北京大学、武汉大学能够出几位与西方主流经济学唱反调的经济学家。

一．引言
    在西方主流微观经济学和宏观经济学的教科书中，到处可以见到关于“均衡”的描述。有人吹嘘：
    “均衡分析作为一种方法，在1947年，被一位精通当时数学各种方法的学生——萨缪尔森在其博士中系统地建立起来。所谓‘系统地’，是说萨缪尔森的工作如此彻底，他运用数学工具于经济分析是如此娴熟，以致今天（90年代）出版的教科书里，这种方法已经被写成可以机械地一步一步执行的‘菜谱’和机程序。人们可以不用任何思维就从输入一组‘数据’得到关于整个问题的解答。……萨缪尔森为此得到了他的诺贝尔奖。”（博客）
    但是“均衡”究竟是什么含义，究竟是怎么定义的，很多学者，依我看，甚至包括诺贝尔经济学奖得主，都是稀里糊涂。难怪老有人问：何为“均衡”？在欧美主流经济学教科书中，有关“均衡”通常是这样解释的：“经济分析中使用的均衡一词，原是从机械力学借用来的一个词语，意指相互作用的力量因大小相等、方向相反而处于静止不变的平衡状态。……因此，经济理论的均衡分析方法，实际上可以归结为，考察供给和需求这两种力量在其相互作用中（1）是否趋向均衡，即所谓均衡的存在性（existence）问题；（2）均衡是否稳定，即均衡的稳定性（stability）问题；以及（3）达到均衡状态所需具备的条件。”（宋承先，1997，第20－21页）由以上引述可知，所谓“均衡”，是指经济系统“处于静止不变的平衡状态”。既然经济学里的“均衡”是从力学里借用过来的，那我们就先回忆一下力学里“静止不变的平衡状态”是个什么概念。
    力学里讲，如果施加于一个质点的合力为零，则该质点处于相对静止或匀速直线运动状态；而如果合力不为零，则该质点的加速度与合力成正比。显然，力学里讲运动状态，一般有三种：静止、匀速直线运动、加速运动；运动并非静止一种。静止和平衡也不是一个概念。静止是指质点速度为零，而平衡是指质点所受合力为零。静止时不一定平衡，平衡时也不一定静止。例如钟摆，当钟摆摆到最高位置时刻，此时速度为零，钟摆瞬间处于静止状态，但此时钟摆所受合力不为零，所以钟摆不会停在最高位置，而是往回摆动。当钟摆摆到最低位置时，按说钟摆应该停在这里，但钟摆也不会停留在这个位置上，因为它要按现在的速度继续往前运动。如果考虑运动有能量损耗，则最低位置是钟摆的稳定平衡位置，因为在这个位置上，当运动速度最后趋向于零时，钟摆上的合力为零；而且，这个最低位置也是稳定的，如果你把钟摆偏开一点，它最终还会回到原来的平衡位置。这样，静止、平衡、稳定是三个不同的概念。西方主流经济学里的“均衡”如果是指“静止不变的平衡状态”（宋承先，1997，第20－21页），这等于说西方主流经济学是研究一只死钟的“学问”，其意义可想而知。
下面我们就以诺贝尔经济学奖得主、美国经济学家索洛（Robert Solow）的新古典经济增长模型为例，说明胡乱套用“均衡”是何等荒谬。

二．索洛经济增长模型的荒谬

    “例3.2.1  Solow 方程给出的人均资本存量的积累方程为
        dk(t)/dt = sf(k)－nk(t) ≡φ(k)，            (3.2.2)
    和初始资本存量k(0)=K(0)/L(0)给定。其中f(k)为人均生产函数，满足性质f(0)=0，f’(k)>0和f’’(k)<0，s为固定储蓄率，n为人口增长率。”“方程(3.2.2)表示人均储蓄用来增加人均资本存量和补偿人口的增长所占有的资本存量。通过这个方程，在给定的生产函数下，可以得到人均资本存量积累的路径。”
“性质3.2.1
    如果生产函数，参数n和s满足0＜n/s＜f’(0)，则存在惟一的k*，满足φ(k*)=0，即系统(3.2.2)存在惟一的均衡点，它为k*。”
“性质3.2.2
    在性质3.2.1的假设下，系统(3.2.2)的均衡点k*是渐近稳定的。即在理性预期的假设下，从任意的初始资本存量出发的系统(3.2.2)的解将收敛到均衡点k*”
    以上引文见（龚六堂，2002，第61－63页）。这个例子“证明”了经济增长系统均衡点的存在及其稳定性。
    下面我们指出索洛（Robert Solow）的新古典经济增长模型的荒谬之处。
    （1）索洛认为经济系统一定要达到“均衡”，均衡时满足dk/dt=0，或φ(k*)=0，人均资本k不随时间而变化，即人均资本保持为常量。人均资本保持为常量，意思是要求资本存量K的增长与劳动力人口L的增长保持同步：人口增长，资本存量也增长；人口下降，资本存量也下降。而事实是，劳动力人口无论是增长、持平或者下降，资本存量都有可能实现增长。索洛的这个结论特别不能用来指导人口已经很多的中国家发展经济，这些国家应该控制人口数量的盲目增长，以便尽可能快地赶上发达国家的生活水平。
    （2）索洛认为，为了实现“均衡”，人口增长率n和固定储蓄率s应该满足不等式0＜n/s＜f’(0)。首先，根据这个不等式，“均衡”要求人口增长率n一定要大于零，等于或者小于零则经济系统不可能达到“均衡”。前面说了，人口数量持平或者适度下降都有可能使经济增长，人们要求的就是经济增长，不“均衡”才是人们期望的经济状况，这样，您要求经济系统达到“均衡”还有什么意义？其次，要求分母上的储蓄率s不能取得较低，特别不能趋向于零，因为这样肯定会使后面的不等式不成立，从而也使经济系统不可能“均衡”。但是我们知道，储蓄率s＝0，表示没有积累，资本存量K保持常量，生产按原有规模进行简单再生产，这在理论上也是一种可能的生产模式。如果资本存量K保持常量，而人口的增长率为n，则人均资本存量k肯定要按指数率衰减：k(t)=k(0)exp(-nt)，最后衰减到零，在理论上这也是一种稳定状态（属于人类应该避免的“均衡”状态）。而根据索洛的经济增长模型，显然得不到上式，因而也解释不了这种经济现象。
    （3）在几乎所有西方经济学教科书中，人们还画出了经济系统趋向“均衡”的收敛轨迹，如果k(t)   （4）根据上面的公式（3.2.2），可以得到“均衡”时的人均产出是：
        y＝f(k*)=(n/s)k*  ―――――――――――――――――――（1）
    根据这个公式（1），人们可以得到这样两个结论：（1）如果人口的增长率n>0但很低很低，则人均产出就会越来越低，而不管人均资本k*是多大。这符合实际吗？（2）如果储蓄率s越来越小，每年的产出几乎吃光用光，没有什么积累，人均产出反而越来越大。这可能吗？这不在骗人吗？
    我这里给出一个人均产出y的公式，起码可以避免以上矛盾，供讨论：
        y=y0exp(s/a－n)t  ―――――――――――――――――――（2）
    这里y0表示初始产出，s为储蓄率，a为资本－产出比率，n为人口增长率，t为时间。这个公式中的人口增长率n可正可负，都解释得通。如果n=0，表示人口数量保持不变，这时y=y0exp(s/a)t，人均产出依靠储蓄积累获得增长。如果储蓄率s=0，这时y=y0exp(-nt)，没有积累而人口如果增长的话，n>0，则人均产出就会下降，这也好理解；而如果人口数量适度下降，n<0，则人均产出也有可能适度增长，这当然也好理解。
    我们再把公式（2）中的各参量的量纲说一下。资本存量K的量纲是“元”，写成式子为：［K］＝元。Y为每年的收入，所以，［Y］＝元/年。根据公式K=aY，a为资本－产出比率，所以，［a］＝年。人口增长率n的量纲，［n］＝1/年。储蓄等于资本存量的增加，应该有下式：dK/dt=sY，所以储蓄率s无量纲。时间变量t的量纲是“年”：［t］＝年。另外，劳动力数量L的量纲是“人”：［L］＝人。人均资本k的量纲：［k］＝元/人，即每人多少元资本。人均产出的量纲“［y］＝元/(年·人)，即每年、每人多少元产出。
    公式（2）的一个明显的特点是不存在稳定的“均衡”点，即没有局限于“静止不变的平衡状态”，增长的经济系统是个不稳定系统。

三．结论

    由以上分析可知，现象和其他现象一样，并非只有“静止不变的平衡状态”可供研究。既然我们研究的是经济增长，那就不应该是“静止不变的平衡状态”，经济总量将会不断增长，不一定非要达到所谓“均衡”。Robert Solow囿于“均衡”，难免要闹出些笑话。难怪有人会说：“我越来越感觉到数学已经成为了经济学家们故弄玄虚的道具”。数学成为经济学家的道具不可取，经济学家必须首先搞清楚自己是在研究什么问题，然后考虑用什么数学工具，不能千篇一律地把所有现实经济问题统统硬塞进“均衡”的框框中。
    本来我想把我的一些不同看法与龚六堂先生交流交流的，后来看见主编邹恒甫先生有言在先：“我们期望同学们指出丛书中的缺点和错误，以便我们在重印和再版时加以修正”。“如有独到见解和发现，望用撰稿给我们主编的Annals of Economics and Finance.”（龚六堂，2002，编者说明）。我既不属于“同学们”，也不会“用英文撰稿”，更不懂得与国际经济学接轨，所以只好作罢。我就怀疑，邹恒甫先生和龚六堂先生的那么多高足中间，许多年来就没有人提出过“独到见解和发现”？德国的资产阶级学校，培养出了马克思、恩格斯这样的无产阶级伟人；苏联的无产阶级学校，方针是“为无产阶级服务”，结果培养出来的许多知识分子“世界观基本上是资产阶级的”；满清的科举制度腐朽透顶，结果还出了个主张维新改革的状元郎谭嗣同。所以，我在这里斗胆狂言，有朝一日，在北京大学、武汉大学的校园里，一定会站出一位或者几位与西方主流经济学唱反调的、不平凡的经济学家。


［1］龚六堂，2002，《动态经济学方法》，北京大学出版社。
［2］宋承先，1997，《西方经济学》，复旦大学出版社。