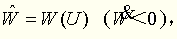广告效果的多级模糊综合评价
[摘要] 广告效果的多层次性使得广告效果具有模糊性。模糊数学中的多级模糊综合评价为广告效果的测定提供了有效的评价途径。运用多级模糊综合评价模型测定广告效果,关键在于设计广告效果综合评价的指标体系和确定各评价指标权重。
[关键词] 广告效果;模糊评价;权重;指标体系
广告效果的测定结果常常差强人意,这源于广告运营的高度复杂性。复杂性意味着因素的多样性,而大量可以精确描述的单因素错综复杂地交织在一起,必然产生出具有新质的属性,即模糊性。模糊性问题应用模糊方法予以解决。由于广告效果包括了多个层次,其构成具有多层次性。本文借鉴多级模糊综合评价来进行探讨。
一、多级模糊综合评价模型
按确定的标准,对某个或某类对象中的某个因素或某个部分进行评价,称为单一评价;从众多的单一评价中获得对某个或某类对象的整体评价,称为综合评价。在实际工作中,评价的对象往往受各种不确定性因素的影响,其中模糊性是最主要的,这样,将模糊理论与经典综合评价方法相结合进行综合评判将使结果尽量客观。而遇到多个带有模糊性的因素,且各种因素又具有不同的层次,而且权重分配又比较均衡的问题时,需要采用多级模糊综合评价来解决。多级模糊综合评价的具体步骤如下:
第一步:建立因素集
因素集是评价对象各个因素组成的集合。设因素集为U=u1,u2,Λ,un,将因素集U=u1,u2,Λ,un按某种属性分成若干组U=U1,U2,Λ,Us,即Ui=Ui1,Ui2,Λ,Uini,i=1,2,Λ,s。
第二步:建立评价集V
评价集是评价者对评价对象可能做出的各种评价结果所组成的评价等级集合。设V=(v1,v2,Λ,vp)。评价等级个数p通常要求大于4而不要超过9,因为,一方面,p过多将超过人的语义区分能力,不易判断对象的等级归属;另一方面,p过少又不合模糊评价的质量要求。
第三步:建立权重集
先设因素类权重集。设第i类因素Ui的权数为ai( i = 1,2,Λ,s),则因素类权重集为:Λ=(a1,a2,Λ,as)。
再设因素权重集。设第i类中的第j个因素uij,则因素权重为:Λi=(ai1,ai2,Λ,aini),i=1,2,Λ,s
权重的确定有Delphi法(专家调查法)、AHP法(层次分析法)等方法,为适合于模糊运算,一般要求权重的分量和为1。
第四步:进行一级模糊综合评价
对每一类的各个因素进行综合评价,设一级模糊综合评价的单因素评价矩阵为:
第i类因素的模糊综合评价为:
B i= Ai OTRi
=(bi1,bi2,Λ,bip)
公式中“O”为模糊矩阵的合成算子。
第五步:进行二级模糊综合评价
二级模糊综合评价的单因素评价矩阵,应为一级模糊综合评价矩阵,因此有:
于是,二级模糊综合评价为:
如果有的子因素集Ui仍含有较多的因素,可将Ui再划分,于是有三级模型。这样依次的划分下去,实际上是对影响因素先分大类,然后再分小类,这样就反映了因素的层次特性。评价时,从最后一次划分的最低层的因素开始,一级一级往上评,直到评到最高层。
二、广告效果综合评价的多级指标体系
广告效果是广告给消费者所带来的直接或间接影响。而这种影响是广泛的、多种多样的。因此,为了有效地对广告效果进行评价,人们常常对广告效果进行的分类,从不同的角度把广告效果分成相互关联的很多种类。每一种类中又包含了许多不同的变量,这就形成了广告效果的多层结构。在这个结构中,各个变量之间是相互关联的。美国南加州大学的杰拉德·丁·泰利斯教授认为,可以把广告的作用看成为一个沟通的过程,有关广告及其效果测量的所有指标可以归纳为广告输入、消费者处理和市场输出三类。具体如下图:
据此,我们把广告效果的等级描述如下:
广告输入指标是配合其他手段如价格、促销和产品质量来说服消费者购买其产品的一种力量,分为广告强度、广告媒体和广告内容三类。广告强度是指广告施加于受众的水平,广告媒体是广告触及受众所要经过的沟通渠道,广告内容是广告的创意质量。
市场输出指广告主引进的消费者或市场需求在行为上的改变。它们可分为品牌选择、购买强度和合计指标三类。品牌选择是指消费者对品牌的取向,购买强度是指消费者一时期中购买某一品牌的程度,合计指标反映了个体消费者选择的集合,如销售数量、收入和利润。
三、广告效果模糊综合评价
根据上面建立的多级模糊综合评价模型和广告效果综合评价的指标体系,我们进行广告效果的模糊综合评价。
(一)建立广告效果模糊综合评价因素集
设U=广告输入,消费者处理,市场输出。将U=广告输入,消费者处理,市场输出分为三组:U=U1,U2,U3,即:U1=广告强度,广告媒体,广告内容,U2=认知,感受,意向,U3=品牌选择,购买强度,合计指标。
(二)建立广告效果模糊综合评价的评价集
因评价的目的是评价广告效果的好坏,因此,设V=(V1,V2,V3,V4),其中:V1表示好;V2表示较好;V3表示一般;V4表示差。
(三)建立广告效果模糊综合评价的权重集
设因素类权重集为:A=(a1,a2,a3),再设因素权重分别为:A1=(a11,a12,a13)、A2=(a21,a22,a23)、A3=(a31,a32,a33)。
假设采用Delphi法(专家调查法)确立权重,经对专家调查结果的统计,得出各因素的权重假设为:A =(0.20,0.35,0.45),A1 =(0.30,0.42,0.28),A2 =(0.20,0.50,0.30),A3 =(0.30,0.30,0.40)。
(四)进行一级模糊综合评价
我们仍然采用Delphi法(专家调查法),请有关专家评价小组对单因素层的各个指标进行评价(打分或投票),对评价结果统计后假设得到如下三个评价矩阵:
为了突出主要因素,采用模型M(∧,∨)进行合成运算,一级综合模糊评价结果。
(五)进行二级模糊综合评价
显而易见,二级模糊综合评价时的单因素评价应为相应的一级模糊综合评价。因此,二级模糊综合评价的单因素评价矩阵应为一级模糊综合评价矩阵。
令总单因素评价矩阵为:
同样采用模型M(∧,∨)进行合成运算,计算二级综合模糊评价结果,则广告效果的综合评价集为:
(六)综合评价结论
按最大隶属度原则,广告效果较好。因为在B =(0.30,0.35,0.30,0.20)中,0.35最大,而0.35对应的评价是较好。
:
[1] [美]杰拉德·丁·泰利斯.广告效果评估[M].北京:劳动社会保障出版社,2005.
[2]胡宝清.模糊理论基础[M].武汉:武汉大学出版社,2004.
[3]李士勇.工程模糊数学及应用[M].哈尔滨:哈尔滨大学出版社,2004.
[4]谢季坚,刘承平.模糊数学方法及应用[M].武汉:华中科技大学出版社,2000.
[5]孔玉生.中小核心竞争力的模糊评价[J].江苏大学学报(社会版),2003,(1).