江苏化工产业集聚度与经济增长的关系研究

　内容摘要：本文以江苏省1993-2003年化工产业集聚度与增长的关系进行实证性研究，并在利用单位根检验对变量平稳性考察的基础上，应用协整方法对变量的长期均衡进行分析，最后对集聚度和经济增长作了回归分析。结果表明，在1993-2003年样本区间内化工产业集聚度与经济增长之间存在长期的均衡关系，集聚度和经济增长存在的不是简单的线性关系，而是三次函数关系。

　　关键词 ：区位商 经济增长 因果关系
　　
　　江苏的沿江开发战略首选的产业是化工产业，规模以上化工增加值占全省规模以上工业增加值的比重由2001年的10.86％提高到2005年的11％，2010年将达到12％；2005年全省化工销售收入预计达到2288亿元；精细化工产品产值率在2005年将达到45％，2010年将达到50％，接近发达国家先进水平；预计2010年石油化工技术水平基本接近国际先进水平，精细化工到2010年将达到17％。由此看来，已经初步形成了化工产业集群。现在长江沿岸化工产业带已经集中了江苏省2/3以上的化工生产能力，形成规模和特色及集群优势有以扬子石化、金陵石化、仪征化纤、南化集团为主体的特大型南京化工生产基地，有南京化学工业园、南京经济开发区化工园区、镇江国际化学工业园、扬州沿江化工区等11家国家级、省级化工园区。
　　江苏的经济增长和化工产业集群的是息息相关，而江苏省化工产业的集聚度与经济增长之间是否保持一种长期的均衡关系，是否具有因果关系，它们之间的回归关系如何，这些都是本文想要解决的问题。
　　
　　产业集群与经济增长分析
　　
　　按照《国民经济行业分类》（GB/T4754-2002）的分类标准，本文研究的化工产业包括化学原料及化学制品制造业、医药制造业、化学纤维制造业、橡胶制品业、塑料制品业五个产业，数据来源于1993~2003年各年度的江苏省统计年鉴。测度化工产业的集聚度，用区位商来表示化工产业的专业化程度和集群状况。区位商的公式如下：
　　
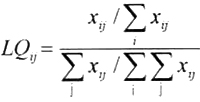
　　式中：i为第i个产业；j为第j 个地区；xij表示第j个地区的第i产业的产值指标；产业规模区位商也称区域规模优势指数，表示该地区该行业的规模在全国的位置。当产业规模区位商大于1时，表明该地区该产业具有比较优势，它一定程度上显示出该产业具有较强的竞争力，产业规模区位商越大，表示该地区该产业的比较优势越显著，竞争能力越强；产业规模区位商等于1时，表示该地区该产业处于均势，该产业的优势还不明显；产业规模区位商小于1时，表明该地区该产业处于比较劣势，竞争能力弱。
　　通过计算，得到化工产业从1993年到2003年的区位商均大于1，表明江苏省存在着化工产业集群，且集聚度年均增长0.41%。但其中医药制造业和橡胶制品业区位商均小于1，没有形成集群。同时，医药制造业集聚度逐年降低，年均增长率-1.92%，而橡胶制品业集聚度逐年上升，年均增长率5.22%。化学原料及化学制品制造业、化学纤维制造业和塑料制品业区位商均大于1，已形成产业集群，并且化学原料及化学制品制造业和化学纤维制造业集聚度逐年上升，年均增长分别为4.67%、4.18%，而塑料制品业集聚度逐年降低，年均增长率-5.56%。
　　江苏省的经济增长用人均GDP来表示，下文主要验证化工产业集群的发展和经济增长的关系。
　　产业集群与经济增长之间的关系，国内外学者有过相应的研究。LuraPaija(2001)通过对芬兰ICT产业集群的实证分析，认为ICT产业集群是芬兰基于知识的经济增长的发动机，优化了芬兰的产业结构，构筑了芬兰国家竞争优势。Leo、Braun和Winden（2001）的研究表明，产业集群对城市或更小的经济区域的经济发展可以发挥决定性的作用。Fan 和Scott（2003）研究了东亚地区和我国的产业集群与经济增长之间的关系，发现二者之间具有双向促进关系，新加坡、香港、上海和北京等城市都利用产业集群策略来吸引外商直接投资，加速地区经济发展。法国的伯兰克在2000年实证研究了IT产业集群，主要包括电缆、电信、互联网、软件、数据处理和计算机系统几个产业在美国各个州区域的比较以及与各个州就业和州经济增长的贡献等等。国内学者对其进行了大量的定性论述，但对因果分析方面的实证研究较少。
　　
　　实证分析
　　
　　20世纪后期，诺贝尔经济学奖获得者、著名计量经济学家格兰杰提出的基于平稳时间序列的因果检验方法，通过解释变量和被解释变量之间的相关性分析，确定变量之间的因果关系，这一研究方法对传统的研究进行了修正，一个完整的格兰杰因果检验过程可描述为时间序列的单位根检验、变量之间的协整和格兰杰因果关系检验。
　　

　　（一）单位根检验
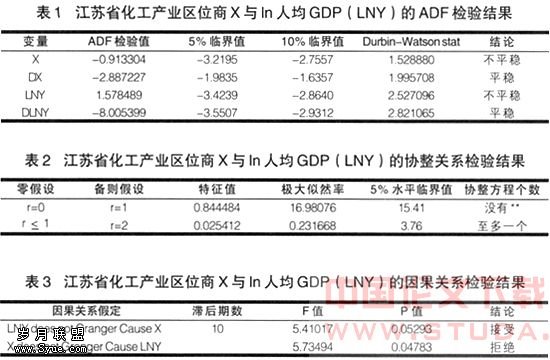
　　检验变量是否稳定的过程称为单位根检验（Augmented Dickey-Fuller Test）。该检验法的基本原理是通过n次差分的办法将非平稳序列转化为平稳序列，具体方法是估计回归方程式：
　　
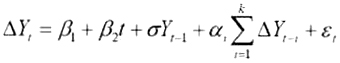
　　其中β₁为常数项，t为时间趋势项，k为滞后阶数（最优滞后项），ε_t为残差项。该检验的零假设 H₀：δ=0；备择假设 H₁：δ≠0。如果δ的ADF值大于临界值则拒绝原假设H₀，接受H₁，说明{X_t}是I(0)，即它是平稳序列。否则存在单位根，即它是非平稳序列，需要进一步检验，直至确认它是d阶单整，即I(d)序列。加入k个滞后项是为了使残差项ε_t为白噪音。
　　（二）协整检验
　　变量序列之间的协整关系基本思想在于，尽管两个或两个以上的变量序列为非平稳序列，但它们的某种线性组合却可能呈现稳定性，则这两个变量之间便存在长期稳定关系即协整关系。
　　Johansen(1988)和Juselius(1990)提出了一种用极大似然法进行检验的方法，通常称为Johansen检验。其基本思路是在多变量向量自回归(VAR)系统回归构造两个残差的积矩阵，矩阵的有序本征值(Eigen value)，根据本征值得出一系列的统计量判断协整关系是否存在以及协整关系的个数。它可用于检验多个变量，同时求出它们之间的若干种协整关系，这也是本文采用的方法。
　　由于使用的是两变量系统，因此零假设为无协整关系H₀：r=0，H₁：r=1，拒绝零假设则表明存在协整关系。极大似然率为16.98076，大于5%水平临界值15.41，所以拒绝零假设，即接受X和LNY存在协整关系。在考虑有协整关系的情况下，进一步检验有多少个协整关系，极大似然率0.231668小于5%水平临界值3.76，所以接受零假设，即存在一个协整关系。
　　（三）因果关系检验
　　协整检验结果说明变量之间是否存在长期的均衡关系，在协整基础上，利用因果分析(Granger Causality Test)对这种关系是否构成因果关系进行研究。格兰杰因果关系检验的基本原理是：在做Y对其他变量(包括自身的过去值)的回归时，如果把X的滞后值包括进来能显著地改进对Y的预测，即X是Y的（格兰杰）原因；类似地定义Y是X的（格兰杰）原因。为此需要构造：
　　
　　即F的统计量服从第一自由度为m，第二自由度为n-(k+m+1)的F分布。若F检验值大于标准F分布的临界值，则拒绝原假设，说明X的变化是Y变化的原因。
　　当显著性水平为5%时，滞后10期时LNY不是X的原因，X是LNY的原因。化工产业的集聚度是人均GDP对数的原因。
　　（四）回归模型建立
　　用SPSS做化工产业集聚度和增长的回归分析，可以看出Cubic曲线的拟和优度最好，通过以上的分析比较，得到人均GDP和区位商之间的关系选择三次函数Cubic来进行回归分析的结论。具体模型为：
　　LnY=51.32-96.92X₂+56.31X₃ ；其中，Y代表人均GDP，X代表区位商。
　　综上所述，本文的结论为江苏省的化工产业集聚度和经济增长不具有平稳性，但是化工产业集聚度和经济增长一阶差分均具有平稳性。协整结果分析，产业集聚度与经济增长之间具有显著的协整关系，这说明它们是一种稳定的长期均衡关系。协整关系所蕴含的长期稳定关系，与集聚度和经济增长的趋势是基本相符的。格兰杰因果检验表明，当显著性水平为5%时，滞后10期时经济增长不是集聚度的原因，化工产业集聚度是经济增长的原因。化工产业集聚度和经济增长存在三次函数回归关系。
　　
　　：
　　1.Van den Berg, L.Braun, E and van Winden, W., Growth Clusters in European Cities: An Integral Approach [J]. Urban Studies, 2001
　　2.李金昌，徐雪琪.浙江省经济增长与收入分配差异实证分析.[J].商业经济与管理，2005（10）