基于GARCH模型族的上海股市波动性分析
摘要:以上证综合指数为研究对象,采用GARCH模型族对2000—2006年上海股票市场的波动情况进行了实证分析。研究表明,上海股市具有明显的ARCH效应,股指收益率具有显著的“尖峰厚尾”特点,存在波动的集群性,市场“杠杆效应”显著,期望收益与期望风险之间存在正相关关系。
关键词:上证综合指数;波动性;GARCH模型族
1 引言
股票市场价格的波动性主要体现在未来价格偏离期望值的可能性,价格上涨或下跌的可能性越大,股票的波动性越大。可以说,股票的波动性代表了其未来价格的不确定性,这种不确定性一般用方差或者标准差来刻画(Markowitz,1952)。
传统的计量模型在描述股票市场收益率时,一般都假设收益率的方差保持不变,但是大量的对股票收益率数据的实证研究结果表明,这一假设是不合理的。大量研究结果表明,股票收益率表现为在某个时间段波动大,而在另一个时间波动段又比较小的现象。对于这种具有“尖峰厚尾、微弱但持久记忆、波动集群”等现象的时间序列,传统经济计量方法要求的同方差性的条件得不到满足,因此运用传统的回归模型进行建模进而进行统计推断往往会产生严重偏差。Engle(1982)[1]首先提出了ARCH模型(Autoregressive Conditional Heteroskedasticity Model),为解决此类问题提供了新的思路。Bollerslev(1986)[2]在Engle的基础上对异方差的表现形式进行了直接的线性扩展,形成了应用更为广泛的GARCH模型。在随后的几十年中,经济学家们又对上述模型进行了扩展和完善,形成了GARCH-M、TARCH、EGARCH等模型,进而形成了一个GARCH模型族。本文即运用GARCH模型族作为工具,对以上证综合指数为代表的上海证券交易所的股票价格的波动性进行了实证分析。
2 模型概述
时间序列的一个显著特点是条件异方差性。Engle(1982)[1]提出自回归条件异方差(ARCH)模型,Bollerslev(1986)[2]将其推广到广义ARCH模型(GARCH)。ARCH类模型现在已被广泛应用于金融计量领域。在波动性研究中最广泛采用的是GARCH模型,其定义由均值方程和条件方差方程给出。
2.1 GARCH(1,1)模型
均值方程:yt=cxt+εt
条件方差方程:ht=Var(εt|Ψt-1)=a0+a1ε2t-1+β1ht-1
其中a1>0,β1>0同时为保证GARCH(1,1)是宽平稳的,要求a1+β1<1。
2.2 GARCH(1,1)-M模型
为了更好地描述金融收益率序列的特征,人们发现随着风险程度的加大,股票收益率也随之加大,为此可以将GARCH(1,1)模型进行推广,允许条件方差对收益率产生影响,这就是由Engle和Robins(1987)等[3]引入的GARCH(1,1)-M模型。
均值方程:yt=c'xt+εt+λht
条件方差方程:ht=Var(εt|Ψt-1)=a0+a1ε2t-1+β1ht-1
当存在风险奖励时,在上述均值方程中当期条件方差的调整系数λ>0;当存在风险惩罚时,在上述均值方程中当期条件方差的调整系数λ<0。
2.3 杠杆效应的TARCH(1,1)模型
资本市场中的冲击常常表现出一种非对称效应,这种非对称效应允许波动率对市场下跌的反应比对市场上升的反应更加迅速,被称为“杠杆效应”。杠杆效应可以通过在GARCH模型中引入一定程度的非对称来实现,即Zako an (1994)[4]引入的TARCH(1,1)模型。
均值方程:yt=c'xt+εt
条件方差方程:ht=Var(εt|Ψt-1)=a0+a1ε2t-1+β1ht-1+γε2t-1Dt-1其中变量Dt-1是表示绝对残差变化方向的虚拟变量,当 εt-1<0时Dt-1=1,当εt-1≥0时Dt-1=0,参数γ允许ARCH效应是不对称的。好消息(εt-1≥0)对条件方差的影响为a1,坏消息(εt-1<0)对条件方差的影响为a1+γ。因此,当γ≠0且统计上显著时,说明信息是不对称的,存在杠杆效应。若γ>0,表明坏消息(εt-1<0)对波动的影响更大;若γ<0,表明好消息(εt-1≥0)对波动的影响更大。
2.4 EGARCH(1,1)模型
Nelson(1991)[5]提出的EGARCH模型或指数GARCH模型清晰地融合了对冲击的非对称反映,形式为

模型中条件方差采用了对数形式,意味着ht非负,且杠杆效应是指数型的。若γ≠0,说明信息作用非对称。如果γ<0且显著,那么坏消息就会有更大的影响。
3 实证分析
本文以上证综合指数为研究对象,选取2000年1月4日至2006年11月7日共1 645个交易日的日收盘指数的数据,分别采用上述模型来研究股价指数的收益率波动特性。本文的资料来源于“大智慧”软件所导出的数据,所使用的分析软件为Eviews5.0。股价指数的日收益率用相邻两天股价指数对数的一阶差分来表示,即Rt=lnPt-lnPt-1,其中Pt为第t日的收盘指数,Pt-1为第t-1日的收盘指数,Rt为第t日股价指数的日收益率。
Rt的各项统计特征如图1所示。图1表现出正的偏度,表明收益率明显右偏;从图1可以看出峰度为8.612198,远大于正态分布的峰度值3,表现出过度峰度,表明日收益率分布与正态分布相比呈现出“尖峰厚尾”的分布特征,反映出股市存在暴跌暴涨现象;Jarque-Bera正态检验统计量相当之大,从而拒绝正态分布的原假设。而从线性的描述了上证综合指数每天收益率的图2中,我们可以看出收益率的波动很大,而且呈现出很明显的波动群聚特征,即大波动之后跟随较大的波动,小波动之后跟随较小的波动。
对样本的日收益率序列进行单位根检验(采用Augmented Dickey-Fuller检验),检验结果显示在1%的显著性水平下,上证指数日收益率序列的ADF检验t统计量的值为-39.40537远小于MacKinnon临界值,从而拒绝原假设,即上证综合指数日收益率序列不存在单位根,是平稳序列。

为了准确地度量上证综合指数日收益率的异方差,在试算的基础上根据赤池信息准则(Akaike Information Criterion)确定了模型的滞后阶数为3阶。对上证综合指数收益率序列利用ARMA(3,0)模型进行回归估计。对回归模型的残差序列进行自相关检验,结果表明,在大部分时滞上,收益率序列残差的自相关函数和偏自相关函数值都很小,表明收益率序列残差并不存在自相关。对残差平方序列进行自相关检验,发现残差平方序列存在明显的自相关。同时,进行滞后3期的ARCH-LM检验,检验结果显示相伴概率P趋近于零,从而拒绝残差序列不存在ARCH效应的原假设,说明上证综合指数收益率序列存在明显的ARCH效应,适宜采用GARCH模型。
由于GARCH(1,1)是刻画条件异方差最简洁的形式,且能很好地拟合许多时间序列,因此我们在实证中采用这一模型,下表列示的是得出的GARCH(1,1)模型族的参数估计的结果:
进一步对GARCH(1,1)模型族拟合结果的残差序列进行ARCH-LM检验,检验结果显示,ARCH-LM检验均接受了不存在ARCH效应的原假设,说明经过GARCH(1,1)模型族的拟合后,明显降低了原序列的波动,而且去掉了其条件方差性。
从下表所列示的GARCH模型族参数估计结果我们可以得到以下几点结论:
(一)GARCH模型族的β1的系数都比较大且通过了显著性检验,说明股价波动具有“长期记忆性”,即过去价格的波动与其无限长期价格波动的大小都有关系。条件方差方程中,系数a1和β1都显著为正,说明过去的波动对市场未来波动有着正向而减缓的影响,从而使股市波动出现群聚性现象。a1+β1都接近于1,这说明股市波动对外部冲击的反应函数以一个相对较慢的速度递减,股市一旦出现大的波动在短期内很难消除。另外,由于GARCH(1,1)、TARCH(1,1)、GARCH(1,1)-M模型中a1+β1小于1,说明收益率条件方差序列是平稳的,模型具有可预测性。

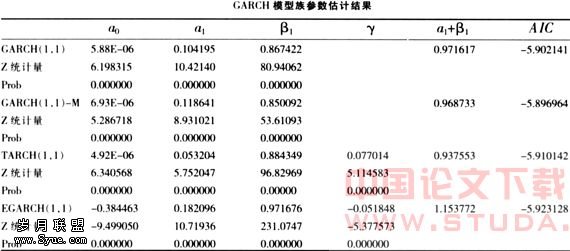
(二)用EGARCH(1,1)模型和TARCH(1,1)模型反映出不同性质的冲击对预期收益的影响是显著不同的,在EGARCH(1,1)模型中γ<0,在TARCH(1,1)模型中γ>0,显示出杠杆效应的存在。显然在上海股市上坏消息引起的波动比同等大小的好消息引起的波动要大,这说明投资者对损失的敏感性要高于同等程度的盈利的敏感性,人们更在乎已经得到的东西。这与美国学家卡尼曼的理论是吻合的。在TARCH(1,1)模型的估计结果中,好消息对ln(ht)条件方差的影响为0.053204,而坏消息的影响为0.130228,不对称效应是明显的。
(三)GARCH(1,1)-M模型中的参数估计结果中,均值方程的ht项的系数是0.180172,在5%的显著性水平下显著大于0,这表明日收益率与市场风险水平呈弱正相关,验证了高风险对应于高收益的投资组合理论。
4 结论
本文以上证综合指数2000年1月4日至2006年11月7日共1 645个交易日的日收盘指数的数据为样本,以相邻两天收盘指数的对数一阶差分来表示股票市场日收益率,通过建立GARCH族模型对股市收益波动性进行实证分析。结果表明:第一,上海股票市场收益率具有显著的“尖峰厚尾”特点,存在波动的集群性,过去的波动对未来的影响是逐渐衰退的,具有波动的持续性。第二,上海股市的波动具有信息不对称性,坏消息引起的波动比同等大小的好消息引起的波动要大,杠杆效应存在。第三,期望收益与期望风险之间存在正向关系。GARCH模型族可以模拟我国上海股市收益的特点。
:
[1] Engle, Robert F. Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K. Inflation. Economet
rica,1982,50:987-1008.
[2] Bollerslev, Tim. Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics,1986,31:307-327
[3] Engle,Robert,David M. Lilien, and Russell P. Robins. Estimating Time Varying Risk Premia in the Term Structure? The
ARCH-Model. Econometrica,1987,55:391-406.
[4] Zako an, J. M. Threshold Heteroskedastic Models. Journal of Economic Dynamics and Control,1994,18:931-944.
[5] Nelson, Daniel B. Conditional Heteroskedasticity in Asset Returns? A New Approach. Econometrica,1991,59:347-370.
[6] 高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2006.











