服装物流业评价指标体系设计的方法探讨

　　[摘要] 物流产业集群指标体系，是实现预测物流产业集群等级这一管理目标的必要手段，本文就服装物流业的自身特点，结合运用层次分析法和模糊综合评价法，对其评价指标体系的设计方法进行了的探讨。
　　[关键词] 指标体系 层次分析法 模糊综合评价法
　　
　　物流产业集群指标体系,是实现预测物流产业集群等级这一管理目标的必要手段,因此,构建合适、的指标体系,显得尤为重要。本文就服装物流业的特点,给出其评价指标体系的设计方法。
　　一、服装物流业的指标体系构建方法
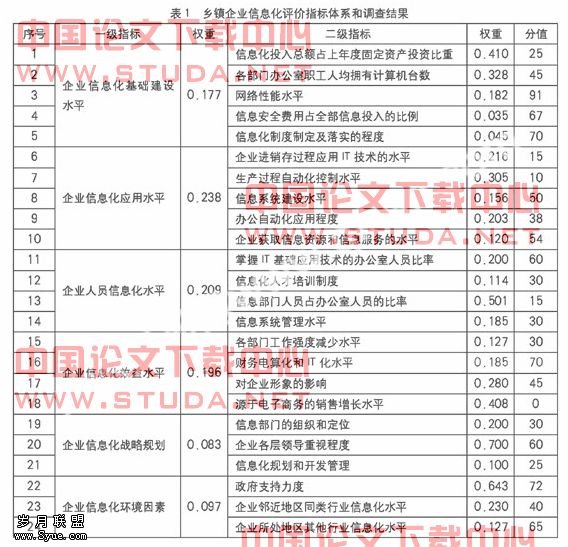
　　由于服装物流业具有依附于服装产业的特性，其指标体系的设计受到服装物流需求、服装物流供给、区域等主要因素的影响，因此，本文结合服装业物流过程中不同阶段的不同特点，另外，全面吸收、归纳物流现有经济评价指标和组织评价指标，根据影响服装物流集群的各个因素的内容、表现、特性及分类重新归纳组合，采取定性和定量相结合的方法来构建服装物流业的评价指标体系，如图1。
　　1.服装物流需求指标体系
　　服装产业聚集的服装企业为了提高经济效益，增强服装设计能力，打造核心竞争力，大多数企业会把服装物流外包给第三方服装物流企业，这就大大促使了服装物流业的发展。所以，服装物流需求的强弱是评价服装物流业的一个重要因素。
　　2.服装物流供给指标体系
　　服装物流业的主体是服装物流企业，而集群区域内服装物流企业的数量，企业之间的竞争合作现状，以及它们的创新能力和提供增值服务能力，投入产出的效率等因素是评价服装物流业的重要因素。另外，集群区域内从事服装物流产业的员工的数量也是评价服装物流业的因素，一般地，测量一个地区产业集群的方法是通过LQ法，即：
　　
　　LQi为服装物流区域聚集系数，ei为i地区的服装物流产业雇员数，e为i地区服装产业雇员数，Ei为全国的服装物流产业雇员数，E全国服装产业雇员数。如果该系数大于1，表明该地区服装物流产业规模较大而且专业化较强，大于全国平均水平。所以，本文把从事服装物流产业的员工数量作为考察服装物流业的一个重要指标。
　　3.区域经济发展指标体系
　　区域经济发展状况，以及政府政策很大程度上影响着服装物流业的发展。道路、服装物流港口的建设等项目，投资巨大，而回收成本时间长，这就需要当地强大的经济实力去投资基础设施建设，以及需要地方政府营造良好的投资环境，吸引跨国服装企业和物流企业在本地扎根，促进本地服装产业和物流产业的发展。而服装物流的发展归根结底是服装物流人才的培养，所以，当地服装物流人才的供给是影响服装物流集群的重要因素。
　　二、服装物流业的模糊综合评价方法
　　1.模糊综合评价方法的基本原理
　　服装物流业的综合评价不但涉及到定量指标，还涉及到定性指标，需要考虑多因素的综合判断问题。针对其多因素、模糊性及主观判断等特点，本文采用模糊综合评价法与层次分析法相结合来评价服装物流业。对定性分析指标采用专家调查的方法，对定量分析指标的处理则引入模糊数学的方法，从而实现定性指标和定量指标的结合。模糊综合评价法的一般步骤如下：
　　(1)确定评价集V并为其赋值U
　　评价集是评价者对评价对象可能做出的各种评价结果所组成的集合，本文采用四等级评价即:V=(V1,V2,V3,V4)二(虚拟，创新，结网,集中）。相应的对不同等级分别赋值即:U=(U1，U2，U3，U4）=(8，6，4，2）。
　　(2)确定模糊评价指标集S
　　设定服装物流业指标体系为评价指标集合，指标集合S由两个层次的因素构成：第一层因素是依据影响服装物流业的因素划分的三个因素子集，即:S=(S1，S2，S3）(服装物流需求，服装物流供给，区域经济发展），第二层因素就是具体的指标。
　　(3)确定各评价指标权重集W
　　在服装物流业指标体系中，不同的评价指标对服装物流业的影响程度也有所不同的，而权重就是反映各评价指标影响程度的重要性尺度。由于评价指标体系是一个递进的层次结构，宜采用层次分析法确定权重，记为:W=(W1，W2，W3），Wk=(Wk1，Wk2，…，Wkn）（k=1，2，3且）
　　(4)确定单因素隶属度矩阵R
　　在模糊集合中，其中的元素与模糊集合存在一定的隶属程度，即隶属度。在服装物流业评价中，指标体系中的各具体指标与影响服装物流业的因素之间的关系用隶属度来表示。具体说来，对Sk中每个因素Sk，按照评价集的评价等级评定出Ski对Vj的隶属度rkij，由此组成单因素评价矩阵Rk，即
　　
　　(5)模糊综合隶属度值集B
　　设某类指标体系Wk中N个指标的单因素评价矩阵Rk，由单因素评价矩阵Rk及评价集U，可得各具体指标评价值: 　　B∶Rk·U=(Bk1,Bk2…Bkn)T公式(6-2)
　　(6)综合评价
　　由Bk及指标权重Wk，可得出各单因素的评价结果
　　Uk∶Uk=Wk·Bk公式(6-3)
　　令B=(U1，U2，U3）,S的综合评价U即评价对象S的最终评价总分:
　　U=W·B=(W1,W2…W3)T公式(6-4)
　　三、评价指标权重的确定
　　对于任何多指标评价系统，各评价指标的相互重要程度即指标权重互不相同,不同的权重对应不同的评价结果。所以,合理地确定指标权重将直接影响模糊综合评价的结果。确定权重,主要是由测评人员根据经验对评价指标体系各项指标重要程度的认识来确定,常用的方法有层次分析法、主观赋权法、客观赋权法等等。
　　本文采用层次分析法和几何平均法确定指标权重，确定评价指标权重的步骤如下：
　　1.引入评价规则构造判断矩阵
　　为了便于，在没有显著性差异的情况下，采用层次分析法近似求解的方法求得指标权重。层次分析法利用1—9标度法（如表6—1）确定测评指标两两之间的相对重要性，使复杂、无序的定型问题能够进行量化处理。
　　该表反映了两个测评指标相对重要程度，利用其对指标Xi和Yj做相互比较判断，使之获得表示相对重要的值aij，从而构成判断矩阵A(其中aij>0且aij=1/aji）。
　　
　　2.计算判断矩阵的最大特征根及对应的特征向量
　　容易验证n是矩阵A的特征值，而权数向量W就是对应的特征向量：
　　 公式（6-6)
　　可以证明,一个n阶倒数对称矩阵的最大特征λmax≥n，证明略。因此本文采用几何平均法来求出重要度矢量，具体步骤如下：
　　(1)计算判断矩阵A各行的各个元素乘积：
　　公式（6-7)
　　(2)计算n次方根
　　 公式（6-8）
　　(3)对向量进行规范化计算：
　　 公式（6-9）
　　其中，矢量W=（W1，W2，…，Wn)为所求特征向量，即所求的模糊指标权重。
　　(4)进行一致性检验。由于主观指标，因此必须进行评分者信度检验，以确定各评分之间是否一致性。其方法是：设A为n阶矩阵，aij则为A的元素，其对任意矩阵A的元素具有传递性，即满足等式：aij×ajK=aiK，则称A为一致性矩阵。一致性检验采用如下公式:
　　CR=CI/RI 公式（6-10）
　　其中:CR称为判断矩阵的随机一致性比率；CI称为判断矩阵的一般一致性指标，它由下式得出
　　公式（6-11）
　　其中：n为A的阶数；
　　RI是随机做出的倒数对称矩阵的一致性指标的平均值；
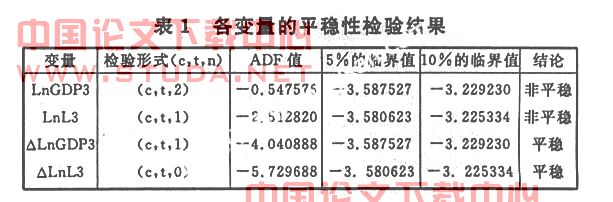
　　具体值，如表1。
　　当CR在10%左右时，一般认为判断矩阵具有满意的一致性，说明权数分配合理。在某些情况下可以放宽至20%，若超过20%，必须调整判断矩阵，直到达到满意的一致性为止。计算CR必须先求出，其公式如下：
　　公式（6-12）
　　式中AWi是AW的第i个元素。
　　3.确定单因素隶属度矩阵
　　在模糊集合中，其中的元素与模糊集合存在一定的隶属程度，即隶属度。在评价中，指标体系中的各指标与总指标之间的关系就用隶属度来表示。隶属度的取值区间为[O，1]，百分之百的隶属关系则记为隶属度R=1，百分之百的不存在隶属关系则记为隶属度R=0。
　　本文采用定性指标的评价，对于定性指标的单因素评价，采用的是模糊统计法。管理委员会或聘请专家根据经验和相关知识，结合时势及企业具体情况，按预先划定的评价等级，就各项指标对企业物流活动中的影响程度进行投票，从而得到模糊评价矩阵R：
　　
　　其中，rij表示对指标xi作出的第j级评语的隶属度，即对指标xi给出等级j的测评人数占全部测评人数的百分比。
　　服装物流产业是一个涉及多学科、多理论的综合课题，本文采用层次分析法和模糊综合评价法相结合的方法构建指标体系、评价物流集群，定量分析结合定性分析，较好的给出了服装物流业评价指标体系的设计方法，对以后的进一步研究给出了一定的思路。
　　:
　　[1]刘成昆王述英:我国物流产业跨越式升级的实现路径[J].流通，2004（9）
　　[2]中国物流报告:2006-2007/中国物流与采购联合会编[R].北京:中国物资出版社.2007，（5）