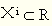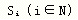毒品走私的行为经济学
【摘要】本文运用行为学中的风险决策论和博弈论,对毒品走私者的风险决策、走私者与禁毒局之间的博弈,以及走私团伙之间的“黑吃黑”现象进行了分析,力图剖析毒品走私背后的经济学动机。对毒品走私的行为经济学分析,将为治理毒品走私提供有益的借鉴。
【关键词】损失规避 混合均衡 进化稳定均衡
毒品经济涉及种植、加工、走私、消费等一系列环节,其中毒品走私环节的利润最大。目前对毒品走私的地下经济学研究主要集中于规模测估、供给与需求、对地上经济影响等领域,对毒品走私的行为分析欠缺。本文从行为经济学的角度对毒品走私行为进行了分析。
一、毒品走私风险决策
毒品走私要承担巨大的风险,研究毒品走私者在不确定条件下的风险决策,主要有三种理论可资借用。
1、期望值理论
该理论假设决策人在不确定性条件下的风险态度是中立的,作决策时只考虑期望值的大小。假设毒品走私者走私成功的概率为P1,收益为X1,走私不成功被抓获的概率为P2,收益(负值)为X2,如果不参与走私将稳定地获得工资性收入w。那么,当且仅当走私的期望收益E(X)=X1P1+X2P2大于w时,走私者才会冒险做出走私的决策,否则他将得不偿失。期望值大小直接反映了走私者动机的强弱,期望概率反映了走私者实现需要和动机的信心强弱。此理论说明:假如走私者把走私的期望效益看得很大,估计实现的概率也很高,那么这个目标所激发动机的力量就很强。
2、预期效用理论
该理论假定,每个决策者都有一个效用函数,效用函数以决策行为可能产生的行为结果为自变量,如果某个随机变量X以概率Pi取值Xi(i=1,2,…,n),而某人在确定地得到Xi时的效用为u(Xi),那么,该随机变量给他的效用便是U(X)= E[u(X)]= P1u(X1)+ P2u(X2)+ … + Pnu(Xn),其中,E[u(X)]表示关于随机变量X的期望效用,U(X)称为期望效用函数。理性的走私者当且仅当走私行为所导致的效用函数期望值大于不走私时所带来的工资效用时,才会选择走私,也就是:U(X)=P1u(X1)+P2u(X2)>U(w)。这个理论强调了走私者主观心理评价,认为走私者是在预期效用最大化的原则下做出决策,而不是根据货币收益的期望值大小来做出决策,突出了走私者做决策的主观预期。
3、期望理论
期望理论认为,人们的决策遵从损失规避准则,而不是风险规避准则。具体而言,大多数人在面临收益时,是风险规避的,在面临亏损时,是风险偏好的。收益和亏损都是相对点而言的,比起收益来,人们对亏损的感知会更敏感。期望效用曲线如图1。
由期望理论,走私者在不确定条件下的决策是以自我感知的亏损和收益为依据的,而不是实际财富拥有的多少。当走私者感知自我财富状态处于亏损状态时,他会“铤而走险”,是风险偏好的;当走私者感知自我财富处于获利状态时,他会考虑“金盆洗手”,是风险规避的。然而走私者对亏损的感知更加敏感,他们的目标追求都是越过参考点O,进入获利状态,选择风险规避。由于参考点是相对于走私者的主观判断形成的,一旦进入毒品走私行业,巨大利润不断诱惑,参考点不断提升,从而很难越过。因此走私者在大部分情况下都处于风险偏好状态,真正“金盆洗手”规避风险的较少。
二、走私禁毒两方博弈
从经济学的角度,毒品走私发生的基本前提是预期风险收益大于合法经营的利润,如果打击惩罚的力度不够,毒品走私活动就难以避免。下面从博弈的角度来分析这一点。
该博弈的参与人是禁毒局和毒品走私者,禁毒局的策略是严打和放松,毒品走私者的策略是走私和不走私。为简化问题,假定禁毒局严打,走私者就一定会被发现,禁毒局放松打击,走私者就不会被发现。其博弈标准式如表1所示。
在上述博弈模型中,Y为财政拨付禁毒局的预算经费(形成收入),C为禁毒局打击走私的成本,F为走私被查获时的罚款(假设形成禁毒局的收入),f为对禁毒不力的处罚(如奖金扣除、职位下迁等),t为毒品走私的投资成本,E为毒品走私成功时获得的高额利润,w为走私者不走私所获得的工资性收入,p为禁毒局严格打击走私的概率,q为走私者选择走私的概率。
对于走私者而言,在给定p的前提下,选择走私的期望收益为U1(p)=(-t-F)p+(1-p)E,选择不走私的期望收益为U2(p)=w,令U1=U2,得到p?鄢=(E-w)/ (t+F+E)。其含义是:如果禁毒局严打的概率小于p?鄢,那么走私者的最优选择是走私;如果禁毒局严打的概率大于p?鄢,那么走私者的最优选择是不走私;如果禁毒局严打的概率为p?鄢,那么走私者随机选择走私或不走私。对于禁毒局而言,在给定q前提下,选择严打的期望收益为U3=(Y-C+F)q+(Y-C)(1-q),选择放松打击的期望收益为U4=(Y-f)q+Y(1-q),令U3=U4,得到q?鄢=C / F+f。其含义是:如果走私者走私的概率小于q?鄢,那么禁毒局的最优选择是放松打击,如果走私者走私的概率大于q?鄢,那么禁毒局的最优选择为严格打击;如果走私者走私的概率为q?鄢,禁毒局随机选择严打或放松。本博弈的混合纳什均衡为:走私者以C / F+f的概率选择走私,禁毒局以(E-w)/ (t+F+E)的概率选择严格打击。
图2中横坐标是走私者选择走私的概率,在(0,1)之间,纵坐标是对应于走私者走私的不同概率,禁毒局选择放松打击的期望收益。Y到Y-f连线上每一点的纵坐标就是禁毒局在走私者选择该点横坐标表示的走私的概率时选择放松打击的期望收益Y(1-q?鄢)+(Y-f)q?鄢。假定走私者走私的概率大于q?鄢时,禁毒局的期望得益为负,于是禁毒局会加大打击力度,因此,大于q?鄢的走私概率对走私者是不可取的。反之,如果走私者走私的概率小于q?鄢时,会使禁毒局选择放松打击的期望收益大于0,从而使禁毒局放松警惕。走私者选择走私的概率会趋向于q?鄢。同理,图3中,p?鄢和1-p?鄢是禁毒局选择严格打击和放松打击的混合纳什均衡的概率,禁毒局选择严打的概率会趋向于p?鄢。
政府为了减少走私而加重对走私者的处罚,即图3中F增加到F',在短期内走私者的期望收益为负,走私者会停止走私,但同时会提高禁毒局放松警惕的概率,从1-p?鄢到1-p',这时走私者的期望值为零,又会选择混合策略,而其混合策略的概率分布取决于图2。只要Y和Y-f的值不变,加重对走私者的处罚虽然在短期内可以抑制走私,使走私的概率小于q?鄢,但从长期来看却只能使禁毒局放松警惕,走私的情况不会得到改善。如果加重对禁毒局的处罚,即图2中f增加到f ',此时,在走私者混合策略不变的条件下,禁毒局不敢轻易放松警惕,走私者在短期内会选择不走私而长期内仍会选择混合策略。走私的概率由q?鄢降低到q',从而达到新的均衡。因此,只有加重对禁毒局的处罚使其尽职尽责,在长期中才会起到抑制走私的作用,这为政府制定政策和规章时带来了有益的思考。
三、“黑吃黑”动态分析
毒品走私中,走私团伙之间时而会发生“黑吃黑”的暴力事件,给社会治安带来了极大危害。下面建立一个博弈模型来讨论走私团伙之间的“火并”策略。
在这个对称博弈中,团伙甲和团伙乙都有可能选择“吃”,即先动手火并,也有可能选择“不吃”,即退让不参与火并。该博弈中有两个完全理性的纯策略均衡:(4,0)和(0,4),另外还存在一个混合策略均衡,即两个团伙分别按一定的概率选择“吃”和“不吃”。设P是选择“吃”策略参与人的比重,则(1-P)是选择“不吃”策略参与人的比重。那么选择策略“吃”的团伙的期望得益是U1=P(-7)+(1-P)4=4-11P;选择“不吃”策略的团伙的期望得益是:U2=P0+(1-P)2=2(1-P);两个团伙的平均得益为:U?鄢=PU1+ (1-P)U2=P (4-11P)+2(1-P)2。
对于走私团伙而言,如果观察到U1>U2,或者U1 基于上述动态学习假设,我们就可以得到选择“吃”的策略动态变化速度的微分方程F(P)=dP/dt=P(U1-U?鄢)=P[(4-11P)-P(4-11P)-2(1-P)2]=P(1-P)(2-9P)。令上式等于0,可得到P1=0,P2=1,P3=2/9三个稳定状态。可以证明,F'(0)>0,F '(1)>0,而F'(2/9)<0。所以该博弈的进化稳定策略为P3=2/9。这表明,当有限理性的走私团伙即使开始不是按照P3比例来选择“吃”的策略,但通过不断学习模仿,选择“吃”策略的团伙的比例会收敛于P3=2/9。选择“吃”的策略的团伙的比例为2/9,也就意味着选择“不吃”的策略的团伙的比例为7/9,这说明当走私团伙遇到利益之争时,大多数理性的团伙会选择温和协商,而少数的团伙则会选择大打出手,进行“火并”。
四、结论
期望值最大化原则、预期效用最大化原则和基于点的损失规避原则,都可在一定程度上解释走私者的风险决策过程。走私者与禁毒局都是以一定的概率做出选择从而达成混合纳什均衡,单纯加重对走私者的惩罚,短期内可抑制走私,长期内则效果丧失;如果同时加重对禁毒局的处罚,则会在长期内有效抑制走私。走私团伙在遇到利益纷争时,会通过模仿学习从而达成进化稳定均衡。
【参考】
[1] 公安部禁毒局网站.
[2] 张照贵:博弈与应用[M].成都:西南财经大学出版社,2006.
[3] 孙绍荣等:理性行为与非理性行为[M]. 上海:上海财经大学出版社,2007.
[4] 于燕京等:禁毒学[M].北京:群众出版社,2005.
[5] 徐兴俊、陈庆彬:犯罪学视野中的地下经济[J].犯罪研究,2006(5).