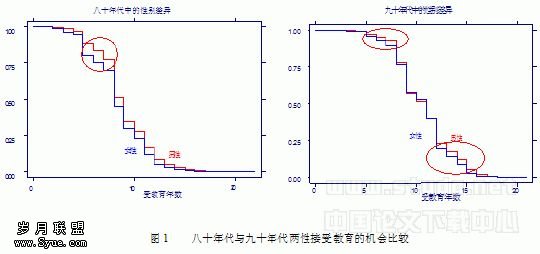
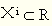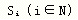马尔柯夫链在预测商品零售价格指数中的应用

                作者：李雄诒　许卫华　王东甫

　[摘要] 根据马尔柯夫链的基本原理，以我国1978年～2004年的商品零售价格指数为实例详细阐述了马尔柯夫链分析与预测的全过程，检验结果表明该模型用于近期预测结果准确可靠，易于操作。
　　[关键词] 马尔柯夫链商品零售价格指数预测
　　商品零售价格指数是反映一定时期内城乡商品零售价格变动趋势和程度的相对数。商品零售物价的变动直接影响到城乡居民的生活支出和国家的财政收入等。同时对商品零售价格指数的预测对的经营决策也起着很大的作用。因此，为准确把握商品零售价格指数的变动趋势，本文利用吸收的Markov链建立一个描述商品零售价格指数变动趋势的分析模型，最后检验结果显示，该模型预测准确，可操作性较强。
　　
　　一、马尔柯夫链简介
　　
　　所谓马尔柯夫链，就是一种随机时间序列，它在将来取什么值只与它现在的取值有关，而与它过去取什么值的情况无关，即无后效性。用数学语言描述，即设{Xn,n≥0}为随机时间序列， E={E1,E2,…,Em}（E为有限个或可列个）为随机变量的状态空间，满足如下条件：
　　每个随机变量Xn只取非负整数值；
　　对任意的非负整数t1＜t2＜…＜m＜m+k，及E1,E2,…Em;Ej，当时，有:

 
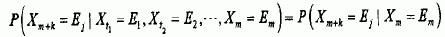
　　则称{Xn,n≥0}为马尔柯夫链。
　　其中马尔柯夫链的概率特性取决于条件概率:
　　P(Xm+k=Ej|Xm=Ei)。
　　P(k)ij(m)=P(Xm+k=Ej|Xm=Ei)为K步转移概率，特别地，当k=1时，Pij(m)=P(Xm+1=Ej|Xm=Ei)为一步转移概率。由转移概率组成的矩阵称为转移概率矩阵，记为：

 
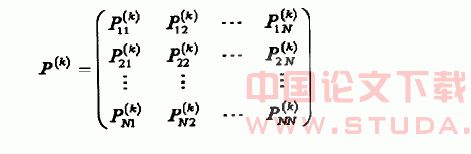
　　为K步转移概率矩阵。同理，当k=1时，为一步转移概率矩阵。且P(k)=Pk。
　　
　　二、应用实例
　　
　　1978年以来，我国商品零售价格指数受市场因素的影响逐年增大，其变化也逐渐呈现出比较明显的稳定性，且市场又是一个随机的动态系统，商品零售价格指数的状态变化究竟受市场上哪种因素的影响是不确定的，因此，商品零售价格指数的高低也呈现出随机性。综合以上特征，可将它视之为一个马尔柯夫链。
　　
　　1.数据的取得
　　数据取自1981年～2002年的《年鉴》和2000年～2003年的《中国统计年鉴》（按1978年=100。其中，1986年、1987年、1988年的数字经过了换算；2004年国内零售物价指数为黄善明在《中国物价》2004年第3期上发表的《影响2004年我国价格走势的因素分析》一文中的估算值）。表1中列出了1978年～2004年我国商品零售价格指数资料。
　　
　　2.确定系统状态及系统状态的初始分布
　　以表1中每年为离散的时间单位。为确保预测的精度和准确度，划分系统状态时应以3～6个为好。本文按照如下标准划分以下5种状态：
　　E1-快速下降（yt-yt-1≤－5）
　　E2－缓慢下降（-5＜yt-yt-1＜0）
　　E3－相对不变（yt-yt-1=0 ）
　　E4－缓慢上升（0＜yt-yt-1＜5）
　　E5－快速上升（yt-yt-1≥5）
　　其中:yt－第t年商品零售价格指数原始值，yt-1－第t-1年商品零售价格指数原始值。所以取E1=快速下降，E2=缓慢下降，E3=相对不变，E4=缓慢上升，E5=快速上升，则该系统的状态空间为E(E1,E2,E3,E4,E5)。由于1979年数据不祥，因此本文以1981年起开始划分状态，根据各状态取值范围确定原始资料各年商品零售价格指数所在状态（表2）。

　　状态概率用状态向量(P1,P2,…Pj)表示，其中Pj为状态是Ej时的概率。表中收集了1978年～2004年的历史资料，由于1979年数据不祥，且本文将2004年的数据作为检验该模型的检验数据不参加过程计算。因此，过程中参加计算的数据是从1981年～2003年共23年的商品零售价格指数值。其中E1＝4，E2＝2，E3＝0，E4＝6，E5＝11。所以各个状态概率分别为:P1=0.1739，P2=0.0870，P3=0.0000，P4=0.2609，P5=0.4783，状态向量π=(0)=(0.1739,0.0870,0.0000,0.2609,0.4783)称为状态的初始分布。

　　
　　3.建立转移概率矩阵
　　在实际问题中，经常近似地用状态相互转移的频率来描述状态转移概率。Pij为i态到j状态的一步转移概率，则:Pij=P(i-j),其中，Mi为系统处于i状态时的样本个数，Mij为样本中由j状态一步转移到 状态的个数。在时，最后一个数据（2003年的数据）不参加计算，因为此时在假定2004年状态未知时，它究竟转到哪个状态尚不清楚。由以上可以算得:
　　
　　
　　4.商品零售价格指数状态预测及检验
　　如果目前预测对象处于状态Ei(i=1,2,3,4,5)，这时Pij就描述了目前状态Ei在未来将转向状态Ej(j=1,2,3,4,5)的可能性。按最大概率原则，这里选择(Pi1,Pi2,Pi3,Pi4,Pi5)中最大者对应的状态即为预测结果。
　　由于2003年的商品零售价格指数状态为缓慢上升状态，而经由一次转移到达5种状态的概率分别为:P41=0.2000，P42=0.0000,P43=0.0000,P44=0.2000，P45=0.6000,由
　　max{P41,P42,P43,P44,P45}=P45=0.6000
　　可知2004年的商品零售价格指数将快速上升，即2004年的商品零售价格指数与2003年相比将会上升，且上升指数的幅度超过5。
　　将预测结果与实际结果比较，由表2可知，2004年的商品零售价格指数状态为快速上升，且由表1中原始数据可得出2004年较2003年商品零售价格指数上升幅度为:357.5-350.5=7＞5符合前述的快速上升的范围。说明预测结果是准确的。
　　同时，在马尔柯夫过程中，不同时期的状态概率由状态向量 表示。且有公式π(n)=π(n-1)P，P为状态转移矩阵。按此公式也可预测出2004年的商品零售价格指数状态向量为：
　　即2004年出现快速上升状态的概率为0.6000，比其他状态出现的概率都较大。因此，2004年是快速上升的可能性较大，这也与前面预测的结果是一致的。同理，按此公式也可预测2005年等近期内年份的商品零售价格指数的状态向量。如2005年商品零售价格指数的状态向量为:

　　结果表明，2005年的商品零售价格指数的变动趋势是出现快速下降状态的概率是0.1945，缓慢下降状态的概率是0.0500，缓慢上升的概率是0.3982，快速上升的概率是0.5564,因此，2005年商品零售价格指数继续出现快速上升的可能性比较大。
　　
　　三、结论
　　
　　经检验，对2004年预测的结果与实际给出的结果是一致的，说明此方法在预测商品零售价格指数时是可靠准确的，并且该方法原理简单，是继时间序列分析和因果分析等方法后又一种预测手段，凡是具有无后效性的序贯动态系统都可用该方法预测。据有较强的可操作性。
　　利用该模型预测分析过程中，得到的结果是区间预测，但不能为提高精确度而设置较多的状态，这样虽然不能得到精确度很高的结果，但却提高了预测的准确度。
　　以上结论都是在状态转移概率平稳的假设下推导出来的，即假定初始状态向量和状态转移概率矩阵保持不变。如果忽视此条件，对本文实例中无限制地预测以后各年份的商品零售价格指数值，将会产生较大的误差。因此要想保证预测准确度，就要不时地根据实际情况适时调整初始状态向量和状态转移概率矩阵。因此，马尔柯夫链法比较适合做近期预测。