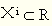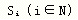时变参数下劳动生产率对经济增长的影响分析
来源:岁月联盟
时间:2010-06-24
[关键词] 时变参数 劳动生产率 经济增长 卡尔曼滤波
一、引言
在传统的经济增长理论中,一般把劳动、资本和科技作为最主要的投入要素,利用索洛增长速度方程研究各要素在经济增长中的贡献,以劳动生产率为研究对象,量化分析劳动生产率与经济增长关系的研究较少,我国是劳动力资源非常丰富的国家,劳动在经济增长中的作用异常重要,分析劳动生产率对经济增长的影响具有重要的理论和现实意义。
通常的研究中,将劳动力因素分解为劳动生产率和劳动参与率,分析劳动力因素对经济增长的作用,一般都是采用最小二乘法估计得到劳动生产率与经济增长率之间的弹性(固定影响系数),即得到两者之间在样本区间内的平均影响关系。实际上,由于经济改革、各种各样的外界冲击和政策变化等因素的影响,我国经济结构正在逐渐发生变化,而用固定参数模型不能完全描述这种经济结构的变化,不能反映解释变量和被解释变量之间逐年的关系变化。因此,本文采用时变参数,建立状态空间模型,利用卡尔曼滤波算法研究劳动生产率增长和经济增长之间的关系。
二、时变参数模型的建立
一般的固定参数模型
Y=KX+C+ut (1)
式中:Y-被解释变量,X-解释变量,K-弹性系数,C-常数项,ut-随机误差项。对于已知的X、Y序列,通过最小二乘法,可以估计出弹性系数K和常数项C(这里K、C估计出来的结果是固定不变的)。本文采用时变参数,建立的状态空间模型和方程(2-1)有所不同:
量测方程:
yt=c0+αtXt +ξt(2)
状态方程:
αt=λαt-1+Л+μt (3)
其中,yt、Xt、代表可观测向量,c0常数项,αt代表状态向量,是不可观测变量,有待估计。这里假设状态向量符合AR(1)过程。λ、Л为AR(1)系数,如果λ估计结果为1,Л估计结果为0,则为随机游走过程。ξt、μt为随机扰动项,假设遵循如下正态分布:μt~N(0,σt22),ξt~N(0,σt12)。量测方程(2)表示了解释变量和被解释变量之间的一般关系,式中参数αt称为状态变量。方程(3)又称状态转移方程,描述了状态变量的生成过程。本文在计算过程中,假定状态向量符合随机游走,带有漂移的随机游走,AR(1)三种形式,计算结果显示,随机游走过程拟合最好,所以本文最终选定了状态方程:
αt=αt-1+μt (4)
三、时变参数模型的估计
1.数据说明
我国劳动生产率的计算公式:
(5)
式中:lp-劳动生产率;y-产出,单位亿元;l-从业人员人数,单位万人。
劳动生产率增长率的计算公式:
(6)
利用上述计算公式,按照1952年不变价格,对我国1952年~2005年间的劳动生产率及其增长率进行计算。
2.模型估计
采用方程(3)和(4)建立的状态空间模型,以GDP增长率为被解释变量,以劳动生产率增长率为解释变量,代入统计数据,采用卡尔曼滤波算法,利用Eviews5.0即可将模型估计出来。限于篇幅,本文略去时变参数估计结果以及方程残差表。
四、模型检验
对于估计结果,用 Eviews 软件对序列GDP增长率和劳动生产率增长率进行 ADF 检验, 检验结果见表1。
由单位跟检验结果,序列GDP增长率和劳动生产率增长率均是同阶单整序列,两者之间存在某种平稳的线性组合。由于不能拒绝时变参数模型的回归残差是平稳时间序列的原假设,因此,可以认为状态空间模型的估计结果是可靠的,说明GDP增长率和劳动生产率增长率之间存在长期的均衡比例不断变化的协整关系,即变参数协整关系。
五、时变参数估计结果分析
根据时变参数模型计算结果分析时变参数趋势图,如图1所示,劳动生产率增长率对于GDP增长率弹性在1953年~2005期间,除了1958年有一个突增而外,基本处于下降状态,尤其在上个世纪九十年代初期下降更快。但是对于GDP增长率始终是正的拉动作用。
样本区间内劳动生产率增长率对于GDP增长率弹性始终是正的,表明劳动生产率增长对于GDP增长具有积极作用。劳动生产率增长带动GDP与其同方向增长,只是不同的年份,劳动生产率增长带来的GDP增长有所不同。
样本区间内,劳动生产率增长率弹性呈现总体下降趋势,劳动生产率增长率每增加1%,拉动GDP增长的幅度降低。说明了劳动生产率增长对GDP增长的拉动作用日益减弱,我国的增长更多的依赖于资本投入和科技水平的提高。
劳动生产率增长率对GDP增长率弹性大于1的年份主要集中在改革开放前和20世纪80年代中后期。改革开放前,劳动生产率增长对于GDP增长的作用比较大,表明当时我国的经济增长中劳动的作用较为显著,经济增长中劳动增长带来的贡献较改革开放后大。20世纪80年代中后期劳动生产率增长对于GDP增长的弹性大于1,表明经过了改革开放初期的尝试性探索,生产力得到解放,经济体制改革的体制因素作用显现出来,劳动生产率的提高对于经济增长的拉动效应增强。随着改革的进一步深化,到了九十年代,劳动生产率提高所能带来的经济增长有所降低,经济增长转向更多地依赖资本投入增长和技术进步上来。
六、结论
本文利用我国宏观经济数据1952年~2005年,了我国的劳动生产率及其增长率,通过引入时变参数,建立状态空间模型,应用卡尔曼滤波算法,计算了劳动生产率和经济增长之间的时变参数影响关系。对于估计结果进行协整检验,验证了模型的合理性。通过对时变弹性的估计结果分析,得出结论如下:
样本区间内劳动生产率增长率对于GDP增长率弹性始终是正的,表明劳动生产率增长对于GDP增长具有积极作用。
样本区间内,劳动生产率增长率弹性呈现总体下降趋势。
20世纪90年代后期以来,劳动生产率提高带来的经济增长有所降低,经济增长转向更多地依赖资本投入增长和技术进步上来。
:
[1]李京文钟学义:生产率分析前沿[M].社会文献出版社,1998年8月第1版
[2]郭庆旺贾俊雪:中国全要素生产率的估算:1979—2004[J].经济研究,2005第6期
[3]田成诗盖美:地区劳动生产率与其经济增长关系的分析[J].生产力研究,2007第8期
上一篇:论奥运经济
下一篇:从市场主体角度谈创意、创造、创新