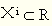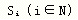经济增长中的“不定性”——经济增长中复杂性的体现
人类社会到21世纪,科技、文化、和社会生活水平也进入了前所未有的崭新阶段。人类几千年的文明积聚了巨大的财富,但稍作统计我们就会发现,这些财富的大部分都集中在美国等发达资本主义国家。如果说是不同的历史和文化背景影响了不同国家的经济发展水平,但是,我们也注意到很多具有相似历史和文化背景的国家和地区,也表现出不同的发展势头。更为奇怪的是,有些几十年前经济水平相当的国家如今却出现了极大的差距。以韩国和菲律宾为例,在1960年,菲律宾和韩国的生活水平是基本一致的,人均资本存量水平按照1975年的价格水平大致都为640美元左右,而且,这两个国家在很多方面也类似,如菲律宾人口是280万人,而韩国是250万人,而且都是一半左右的人口处于工作年龄。按人口的分布,27%的菲律宾人口生活在马尼拉,28%的韩国人口生活在汉城,两者的地理位置差异也不大,但是,从1960年到1988年的近30年内,菲律宾的人均GDP年增长率为1.8%,而韩国的人均GDP年增长率为6.2%。为什么会出现这种现象呢?这正是经济学家要探讨的问题,也是宏观经济学的重要研究课题之一。在新古典的生产函数和效用函数的假设下,传统的经济学模型,如Solow模型、Ramsey模型和Sidrauski模型等,它们给出的结论都是存在惟一的均衡点,也就是不论国家和地区,他们的初始条件如何,只要这些国家具有相同的禀赋特征和文化特征,他们最终会收敛到相同的经济均衡点。因此,这些模型显然不能用来解释上面出现的大量的经济学现象。为此,经济学家们致力于寻找能够解释这些现象的模型。目前出现的主要理论有:Kurz 1968年的模型和1988年之后出现的以Lucas为代表的模型。
一、Kurz模型
1968年Kurz以及后来Zou(1994)在Ramsey模型中引入了财富来讨论消费者的消费路径和资本存量的积累过程,他们的分析过程与传统的Ramsey模型的区别是把效用函数的形式改变为,其中c为消费水平,k为资本存量水平,r为参数,它的大小度量了人们对社会地位或者财富的看重程度。而且,假设消费者从资本(或者财富)和消费品中获得正的、但是递减的边际效用,即u'>0,
同样还假设Inada条件成立。其余的假设和模型的导出和Ramsey模型一致。在这个模型中如果选取特殊的生产函数和效用函数:f(k)=0.30.45,v'/u'=0.3c0.7/0.2k0.2,和人口增长率n=0,参数γ=1和贴现因子pβ=0.3796,可以得到资本存量的三个均衡值分别为Lk1=6.25,k2=10.75和k3=19.75。而且,可以证明均衡点k1=6.25和k3=19.75为系统的鞍点稳定的均衡点,而k2=10.75为系统的完全不稳定均衡点。因此,当初始资本存量水平小于10.75和小于6.25时,资本存量和消费水平会单调下降收敛到均衡点k1=6.25;当初始资本存量水平大于k2=10.75和大于19.75时,资本存量和消费水平会单调上升收敛到均衡点k3=19.75。
它可以用来解释初始条件的不同的两个国家出现经济发展路径差异的原因:如果一个国家的初始资本存量低于第二个均衡点的资本存量水平k2=10.75时,均衡时的资本存量将会收敛到较低的均衡资本存量水平;如果初始资本存量水平越过k2=10.75,均衡时的资本存量水平将收敛到高很多的均衡资本存量k3=19.75。这样,就可以解释不同国家因为初始的资本存量的不同,导致均衡资本存量的不同,从而出现经济增长路径的差异。进一步地说,这个模型也可以解释“贫困陷阱”的现象:两个国家虽然初始资本存量相差不大,但最终的资本存量可能相差很大。如:一个国家的初始资本存量水平稍微低于资本存量水平k2=10.75,而另一个国家的初始资本存量水平稍微高于资本存量水平k2=10.75,但是,这两个国家均衡时的资本存量可能相差很大,前一个国家的资本存量收敛到较低的资本存量水平,后一个国家的资本存量水平收敛到较高的资本存量水平。
二、引入内生休闲及外部性的内生不定性模型
上面引入的Kurz模型虽然可以解释不同的初始条件可以收敛到不同的均衡状态,但是,我们也应当看到Kurz模型解释现象的局限性,如:两个国家的初始资本存量相差很大,但是如果他们都在三个均衡点的同一侧,最终这两个国家也会收敛到相同的均衡资本存量。它当然也不能解释具有相同的初始条件的经济为什么会出现差异的原因。为此,1988年Lucas在内生经济增长模型中引入物质资本和人力资本的积累来分析产生增长差异的成因。他从三个方面分析了出现上面这种经济增长差异的原因。他首先认为是各国消费者的偏好和技术水平的差异影响增长,其次是外生决定的国家宏观经济政策的不同也对经济增长造成差别,最后,是那些持久的、较大的特定外生冲击波及了经济增长。而且,Lucas从古典的增长路径的收敛特点猜测“从非均衡状态收敛到均衡状态的路径是惟一的”。固然,这些外生因素和外在的不定性都可能对经济增长产生影响,但同时我们更感兴趣的是经济系统内生的一些因素对经济增长的影响,如何才能从经济系统内生导出增长的差异性呢?在Lucas之后,很多经济学家对这一问题进行了研究,发现I Lucas在1988年给出的猜测是错误的,即从非均衡状态收敛到均衡状态的路径不一定是惟一的,有很多条甚至是一个连续的路径,这就是经济系统本身的不定性的体现。目前人们研究经济系统的不定性主要体现在:(1)存在多重经济增长路径,在一定的条件下通过内生增长模型会出现和Kurz模型类似的多条平衡增长路径的现象。这样就可能解释不同的国家,虽然具有相同的技术和偏好,但是由于初始的条件不同,他们会收敛到不同的平衡增长路径;(2)在同一条平衡增长路径上,存在多条从非均衡收敛到均衡路径,这就出现了增长路径的不定性。有了这种不定性就可以很好地解释不同的国家虽然初始条件、技术都相同,从而他们具有相同的平衡增长路径,但是,对于每一条平衡增长路径,不同的国家可能选择不同的从非均衡状态收敛到均衡状态的收敛路径,从而也会出现经济增长的差异。
讨论出现这些不定性增长路径的很多,如:Xie(1994)在Lucas给出的具有物质资本和人力资本的两部门的模型中,考虑当人力资本具有外部性影响时,给出了显示的人力资本存量、物质资本存量的显示路径,他得到了同一条平衡增长路径出现的多条收敛路径的情形。这种不定性是经济系统内生具有的局部或全局的不定性。之后,Benhabib(1994)在Lucas模型的基础上引入了休闲,消费者通过选择休闲、物质产品生产时间和人力资本积累时间,也得到了经济增长的不定性,他指出即使是处于相同初始条件、有相同初始禀赋的国家,也可能以完全不同的速度消费以及配置人力资本生产时间和物质资本生产时间。这一结果可以用来解释丰富的经济现象,经济系统的这种内生不定性使得各国之间的经济赶超成为可能。
下面综述了Lucas、Benhabib和Xie等的工作,并采用数据对他们的工作进行了具体的分析;同时,在内生增长模型中引入环境污染、政府公共开支、健康投资等因素出现经济增长的不定性。
(一)Benhabib模型
把休闲引入经济具有重要的经济学背景,70年代,Brock把休闲引入效用函数来解释政府行为对就业水平的影响。目前,在RBC理论中,人们常常用来解释经济周期的成因,一般地说,人们得到商业周期中产出波动的2/3左右可以用劳动供给时间的多少来解释,劳动是宏观经济周期波动的重要因素。它也是税收理论的相关因素,对劳动的征税可能使个人调整工作时间,进而影响产出、财政收入、税收政策等。消费、休闲、工作时间和受时间之间的配置如何共同决定经济的长期增长及其动态过渡过程,近来也受到了广泛的关注。下面以Lucas和Benhabib模型为基础,构造一个引入休闲和人力资本外部性的模型。假设消费者的效用函数定义在他的消费水平c和休闲上,假设消费者从消费和休闲中得到正的效用,而且他们的边际效用是非负和递减的,数学表示为U(c,L),在效用函数的二阶连续可微的假设下,上面的条件可以表示为Uc>0,UL<0,Ucc<0,ULL<0。假设产出由厂商投入物质资本k和人力资本h生产,生产函数为F(k,h)=Akαhβγαuω,其中α+p+ω=1,它表示厂商的生产是规模报酬不变的。u是用于物质资本生产的劳动时间,它在生产函数中的份额与外在人力资本的份额不同。hα是人力资本的平均水平,体现人力资本的外部性。在Lucas中hα是导致不定性的重要因素,而在此处引入内生劳动选择的模型中,即使没有人力资本外部性也可以得到不定性。假设人力资本的生产函数为G(k,h)=δhθh1α-θ(L-u)φ(L-u)ζα,其中θ+φ=1。h1α-θ和(L-u)ζα分别表示人力资本外部性和劳动外部性的影响。假设贴现率ρε(0,1),消费者的最优行为就是在自己的预算约束和初始条件下选择自己的消费路径、休闲路径、和人力资本、物质资本的积累路径来极大化自己的贴现效用和,即:
max∫∞0U(c,L)e-ρtdt (1)
受约束于下面的预算约束方程和给定的初始资本存量k(0)=k0>0和h(0)=h>0。
k&=Aαhβhγαuω-c (2)
h&=δhθh1α-θ(L-u)φ(L-u)ξα (3)
通过哈密尔顿系统,可以得到最优性条件。在均衡时,人力资本和人力资本的平均水平相等,用于人力资本生产的劳动力水平与平均水平也一致,即:h=ha,(L-u)a=L-u。通过最优性条件可以求出k(t),h(t),c(t),L(t)和u(t)的积累方程,从而得到它们在平衡增长路径上的特征。在平衡增长路径上,k(t),h(t)和c(t)分别按不变的速度ψk,ψh和ψc增长,而u和L收敛到常数。我们可以证明得到ψk =ψc和ψk=(β+γ)ψh/(1-α)。为求出显示的平衡增长路径,本文选取特殊的效用函数
出现不定性的情形取决于φ+ζ的大小。如果φ+ζ<1,系统有惟一的平衡增长路径;如果φ+ζ>1,系统或者有两条、或者没有平衡增长路径。由凹性要求φ+θ=1,可知平衡增长路径的条数取决于外部性参数ζ。表1给出的数值分析发现,当φ+ζ>1时,对劳动弹性参数ε的不同取值,都存在惟一的平衡增长路径,而且对应的特征根都是两根为正,一根为负,因此是确定的。当φ+℃>1时,对φ的每一取值的两条平衡增长路径中,其中一条路径的增长率总是为零或接近于零,对应的特征根中有两个正特征值、一个负特征值,它总是局部确定性的。另一条平衡增长路径对于较小|ε|是局部不确定的。这取决于劳动外部性ξ与劳动跨期替代弹性ε之间的权衡,一般而言,较高的|ε|要求较大的ξ才能得到不定性。
表1:平衡增长路径的特征
特征根实 特征根实
δ L*1 u*1 ψ1 部的符号 L*2 u*2 ψ2 部的符号
-0.6 0.439 0.413 0.0006 - ++ 0.476 0.398 0.0024 -- +
-0.7 0.450 0.438 0.0002 - ++ 0.526 0.404 0.0033 -- +
-0.8 0.467 0.460 0.0001 - ++ 0.562 0.411 0.0047 - ++
-2.0 0.630 0.630 0.0000 - ++ 0.760 0.462 0.0097 - ++
-100 0.881 0.881 0.0000 - ++ 0.939 0.515 0.0138 - ++
其中参数A=1,p=0.25,ω=0.25,α=0.5,γ=0,δ=0.05,υ=0.025,θ=0.1,φ=0.9,ζ=2。
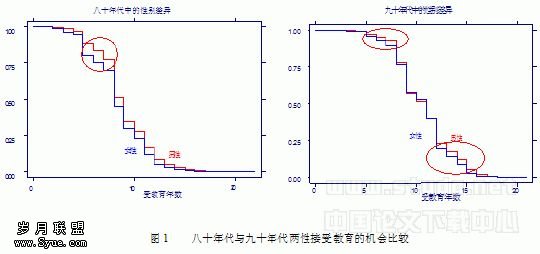
1994年Xie在Lucas模型中,对特殊的效用函数和生产函数得到了显示的资本存量(人力资本和物质资本)、消费水平的路径。通过这些显示解,我们可以很好地理解不定性的含义。假设存在两个国家的,分别叫做国家1和国家2,不妨把美国当作国家1,把1960年美国经济作为初始状态,即t=0,并且把人均资本存量被标准化为10,平均人力资本水平被标准化为1。按照Xie给出的定理,在特定的参数范围下,对于初始资本存量和人力资本水平(k0,h0),存在一个均衡的连续统,我们可用初始时刻投入物质产品生产的时间比例u0对其标序,即可用{u0:u0∈(0,1]}表示,均衡时的用于产品生产的时间比例u*位于区间(0,1),对于任意u0∈(0,1],当时间t趋于无穷大时,u(t)在均衡时趋于u*。这样,对给定美国的初始禀赋条件Lk0=10,h0=1,对于不同的u0,都可以找到一条收敛于u*的均衡路径。为了更好的分析。我们用图1来表示收敛路径。在图1中,我们给出了国家1的三条均衡路径。假设Z1,Z2分别是社会总资本存量k和人均人力资本h的函数Z1=e-(k+n)tk,Z2=e-vth,其中n是人口增长率,k=v(1+ψ-p)/(1-p)和v=6(1-u*)。显然,Z1下降并不意味着资本存量k本身下降,而是资本存量以低于其长期增长率k+n的速度增长;Z2也可类似解释。当u0=u*=0.82时,Z2在均衡路径上是常数,Z1单调递减并收敛到4.669,这条均衡路径在图中表现为一条垂线。当u0=0.75u*时,Z1和Z2都下降并分别收敛到3.872和0.878。
对于国家2,假设它与美国有相同的参数值,不同仅在于它在1960年的初始禀赋(k0,h0)=(1,1),也就是说国家2初始比美国穷。图中给出了国家2的5条均衡路径,其中三条收敛路径对应的人力资本生产时间分别等于0.82,0.75,0.90。由于Z1,Z2在稳定状态的值仅依赖于h0和u0,而与k0无关,国家2的上述三条均衡路径将分别收敛到国家1相应均衡路径的稳定状态。另外两条均衡路径的u0分别等于0.7和0.95。上图表明,如果国家2选择u0=0.7或者u0=0.95的路径,则不论国家1选择这三条路径中的哪一条,国家2都将相应地赶超或者滞后于美国的经济。例如,若国家2沿u0=0.7的路径,国家1沿u0=0.75的路径,则通过可以发现,24年后国家2将在Z1,Z2(或等价的,在k和h)上都超过国家1。也就是说,具有较低的初始物质资本和人力资本禀赋的国家,如果初始投入更大比例的时间进行人力资本积累(u0较小),它将赶超那些有更高初始禀赋的国家。这个模型可以用来解释日本、韩国、新加坡等新兴国家的“奇迹”。
(二)其它的不定性模型
在经济模型中引入环境和健康投资的分析,Barro等已经作了简单研究。目前,世界银行也开始注意环境和健康投资对经济的影响。事实上,目前西方国家的健康花费几乎占其GNP的8-9%,比支出所占GNP的6-7%还要多。如前所述,人力资本被普遍认为是经济增长的重要推动力,相比而言,健康支出也应该对经济增长具有重要意义。直观的说,尽管人力资本会促进经济,但倘若没有健康的身体,个人也无力将人力资本转化为生产实践,按Grossman(1972)的观点,健康对劳动的生产率具有正的作用。重视健康所带来的寿命的延长也能使人力资本存量积累达到新的高度,它可以间接地对经济增长发挥作用,在交替叠代模型中,它也会产生诸如老龄化等问题。随着社会的进步,理性化个人也会越来越追求生活的质量,关注自身的生存状况,健康理应成为消费者的偏好之一。因此,将健康引入经济增长具有重大价值。Gong和Zou(2001)考虑了健康和内生增长的问题。假设消费者的效用函数为CES型:U(c)=(c1-θ-1)/(1-θ),其中θ为跨时期替代弹性。
我们将健康直接引入生产函数,假设产出y由物质资本k和健康资本h生产,假设生产函数y=Akβh1-βp,其中A和pε(0,1)为正常数。这样,物质资本的积累方程为:
k&=Akβh1-βp-δkk-c (5)
另一方面,消费者通过消费增加其健康资本,同时界新陈代谢的使得健康资本发生折旧。这样,健康资本的积累方程为:
h&=Bc-δhh (6)
其中β是正常数,表示消费的边际生产率,δk和δh分别是物质资本和健康资本的折旧率。
消费者的最优化问题就是在约束条件(5),(6)和初始条件k(0)=k0和h(0)=h0下,选择消费、物质资本和健康的路径,来极大化他的贴现效用和∫∞0U(c)e-ρtdt.
通过计算,可以求出均衡时的物质资本-健康资本比率、消费-健康资本比率及增长率的动态方程。通过数值计算和比较得到:
1.若取δk=0.1,δh=0.2,A=0.7,p=0.5,θ=0.1,B=0.9,ρ=0.01,我们得到均衡时物质资本-健康资本比k/h=8.43868,消费-健康资本比c/h=0.304844,储蓄-人力资本比s/h=1.72861。在平衡增长路径上,消费、物质资本、健康资本的增长率为0.104844。也可得出它们的动态过渡方程。比较静态分析发现,随着消费的边际生产力B增大,稳定状态的k/h,c/h都下降,s/h上升,&/c的增长率也增大。
2.若取δk=0.1,δh=0.2,A=0.7,pβ=0.5,θ=2,B=0.2,p=0.01,可以得到三条平衡增长路径。在每条路径上的物质资本-健康资本比率、消费-健康资本比率及增长率分别为:1)(k/h)*1=6.77,(c/h)*1=1.06,γ*1=0.012;2)(k/h)*2=9.37,(c/h)*2=1.01,γ*2=0.002;3)(k/h);=6.54,(c/h)*3=1.07,γ*3=0.013。
因此,对于不同的国家和地区,由于初始条件的不同,经济可能沿不同的路径,按不同的速度,收敛于不同的均衡状态。我们也可在模型中引入税收,考虑消费税、收入税等对经济的影响。取单一均衡路径采用的参数,可以得到消费税税率和收入税税率改变对均衡时的经济增长率、物质资本-健康资本比率、消费-健康资本比率、储蓄-人力资本比率之间的关系。比较静态分析发现,随着消费税的增加,均衡时的上述变量值均下降;随着收入税的增加,增长率和均衡时的消费-健康资本比下降,而均衡时的物质资本-健康资本比、储蓄-人力资本比将上升。当然,我们也可以考虑对应每一条平衡增长路径的特征根的符号,从而收敛路径的多重性。
三、
以上我们分析了经济增长中不定性的内生形成机制。总的说来,在经济增长模型中,系统出现的内生不定性是经济不定性的重要来源。系统的稳定状态本身可能不是惟一的,或者均衡点具有不稳定性;经济的平衡增长路径可能有很多条,而对于同一条平衡增长路径,从不均衡到均衡的路径也可能有多条。对于那些初始条件相当的国家,人力资本投入的不同或外部性的差异,都可以使它们处于完全不同的均衡路径。而某些初始经济基础较差的国家或地区,若采用一定的国家干预或相应的人力资本、产业结构政策,也可能使穷国赶超富国成为现实。在传统经济理论中,静态分析是经济分析的主流,经济现实被极大地抽象化和简化。随着动态经济理论的发展,人们开始运用动力系统、随机方程等数学物理工具和计算机来描绘、模拟经济现象。它不仅可以分析经济在达到均衡状态时的特性,而且可以模拟经济从非均衡状态到均衡状态的动态过渡过程。80年代末,几位诺贝尔奖获得者和数学大师相继提出,经济可以看作一个演化着的复杂系统。经济不是确定的、可预测的、机械的,而是过程依存的、不可完全预测的、有机的演化系统。经济系统本身的复杂性特征决定了它具有内生的不定性。在经济错综复杂的演化过程中,不同特征或不同初始条件的经济体应有相对不同的运行规律,如何找出这些规律并加以运用是一个重要的研究课题。
:
①R. E. Lucas, 1988, On the Mechanics of Economic Development, Journal of Monetary Economics 22:3 - 42.
② Benhabib and R. Perli, 1994, Uniqueness and Indeterminacy: Transitional Dynamics in a Model of Endogenous Growth, Journal of Economic Theory 63:113 - 142.
③adron-de-Guevara, S. Ortigueira,and M. Santos, 1999, A Two - Sector Model of Endogenous Growth with Leisure, Review of Economic Studies 66:609 - 631.
④Danyang Xie, 1994, Divergence in Economic Performance: Transitional Dynamics with Multiple Equihbfia, Journal of Economic Theory 63:97 - 112.
⑤Liutang Gong and Heng-fu Zou, 2001, Capital and Arms Accumulation with Indeterminacy, Mimeo, Peking University, Wuhan University, and the World Bank.
⑥Liutang Gong and Heng-fu Zou, 2001, Health and Endogenous Growth, Mimeo, Peking University,Wuhan University, and the World Bank.
⑦S. Harrison, 2001, Indeterminacy in a Model with Sector- Specific Externalities, Journal of Economic Dynamics and Control 25:747 - 764.