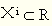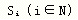经济运行的数学分析
研究社会现象的趋势和发展速度,历来受到各国经济、统计学家的重视,被列为重点研究课题。而迄今为止,动态分析理论本身所具有的局限性,使得经济、统计学家及统计工
常常处于一种难于解脱的困境与矛盾之中。简单地说,具体表现在:(1)没有同“累计法”平均发展速度相对应的平均增长量的概念和公式; (2) 对含有负数的时间数列无法进行速度分析;(3) 根据平均增长量、“水平法”平均发展速度得出的结论经常与事实相悖。本文将针对这些问题,提出和引进新的概念与方法,对动态分析的理论基础重新进行考察,以解决上述出现的和现实经济生活中存在的问题与矛盾。
一、动态分析的分类方法
为了论述的方便,在这里把经济时间数列的发展变化称做经济运行。在对经济运行动态考察分析时,以下将采用类似于物中考察物体直线运动时的那种处理方法,即首先抛开本文是《经济运行的定量分析与系统分析》课题报告的主要内容,此课题曾荣获国家统计研究成果奖,本文有所增删。具体研究对象,把经济时间数列抽象成一个没有质的差别的时间数列。然后在增长量分析中,以逐期增长量为标准;在速度分析中,先把发展速度从标量定义引伸为矢量定义,再以环比发展速度为标准。对经济运行进行分类考察,并给出相应的运动。
二、经济运行的增长量分析
在下面的增长量分析中,以逐期增长量为标准,对经济运行的方式进行分类考察,共有三种运行方式:
(一) 恒量运行
一个经济时间数列a0,…,an-1,如果它的各期发展水平都相等,这种运行就叫做经济的恒量运行,简称恒量运行。即:
ai=aj (i,j=0,1,…,n-1) (1)
(二) 匀增长量运行
一个经济时间数列,如果它的逐期增长量都相等,这种运行就叫做经济的匀增长量运行,简称匀增长量运行(从数学角度看,此时构成一等差数列)。即:
d=ai+1-ai (i=0,1,…,n-1) (2)
或 aj=ai+(j-i)d (i,j=0,1,…,n-1) (3)
此时逐期增长量d为一常数。
平均发展水平(序时平均数)a的公式可简化为:
∑ai a0+an-1
a=───── (i=0,…n-1) (4)
n 2
累计和S的公式可简化为:
n(a0+an-1)
S=───── (5)
2
十分显然,恒量运行就是增长量为0的匀增长量运行,是后者的特殊情形。在公式(3)中,如果令j=n-1, i=0。
an-1-a0
则 d=──── (6)
n-1
这就是现有经济统计原理中的平均增长量的计算公式,但它仅仅适合于匀增长量运行。而无论恒量运行还是匀增长量运行,其平均增长量就等于逐期增长量,因此,此时没有必要专门讨论其平均增长量。
(三) 变增长量运行
一个经济时间数列,如果它的逐期增长量不相等,这种运行就叫做经济的变增长量运行,简称变增长量运行,其逐期增长量是一个变量。经济的恒量运行和匀增长量运行,都是对实际经济运行理想化的抽象,在经济生活一般是不存在的。现实经济生活中,大量的、最为普遍的是变增长量运行,对于这种运行方式,如何说明在一定时期内平均每期增长的数量呢?假设从a0到an-1有平均增长量d,则d满足下列方程:
(a0+d)+…+(a0+(n-1)d)=∑ai (7)
2∑(ai-a0)
即d=───── (8)
n(n-1)
这种平均增长量计算方法的实质:从发展水平看,是要求各年根据 d所推算的累计总和与各年实际所具有的水平总和相一致,见方程(7);从增长量看,是要求各年根据 d推算的累计增长量总和与各年实际累计增长量总和相一致。即:
d+2d+…+(n-1)d=∑(ai-a0) (i=1,…,n-1)
十分显然,匀增长量运行就是逐期增长量为常数的变增长量运行,是后者的特殊情形,所以公式(8)才是普遍适用的平均增长量的计算公式。为了区分说明这个平均增长量和现有经济统计原理中的平均增长量之间的实质性差别,把前者定义的叫做“累计法”平均增长量,简称累计平均增长量,而把后者定义的叫做“水平法”平均增长量。
在此,值得说明的是,上述的讨论适用于包含有零值负值的时间数列,无论它们是出现在基期、报告期,还是中间发展水平。
三、发展速度的矢量定义
经济时间数列负值的存在性,迫使人们思考此时的速度分析方法。如何给出一个包含负数时间数列的发展速度呢?其实答案非常简单,即只要把发展速度从原来的只有大小没有方向的标量定义,引伸为现在的既有大小又有方向的矢量定义,则问题将迎刃而解。即发展速度仍是报告期发展水平和基期水平之比,它是表明社会经济敁发展方向敋和发展程度的相对指标。
报告期水平 aj
发展速度q=─────
基期水平 a0
下面根据基期a0 的正负,分别讨论发展速度q所代表的经济涵义。为使讨论叙述方便起见,不妨假设时间数列代表某的利润额。
⒈ a0>0,基期盈利。
(1) aj>0,报告期仍盈利,发展速度q>0;此时恰好就是现有统计理论中的发展速度,称为第一类正发展速度,简称发展速度,说明企业在基期与报告期都盈利。它是一种最为常见的发展速度。
(2) aj=0,报告期利润额为零,发展速度 q=0;称为第一类零发展速度,说明企业由基期的盈利转变为报告期的零利润额。
(3) aj<0,报告期亏损,发展速度q<0;出现负发展速度,称为第一类负发展速度,说明企业由基期的盈利转变为报告期的亏损。
⒉ a0<0,基期亏损。
(1) aj>0,报告期盈利,发展速度q<0;也出现负发展速度,称为第二类负发展速度。说明企业由基期的亏损转变为报告期的盈利,同第一类负发展速度的经济含义完全相反。
(2) aj=0,报告期利润额为0,发展速度 q=0;称为第二类零发展速度,说明企业由基期的亏损转变为报告期的零利润额。
(3) aj<0,报告期继续亏损,发展速度q>0,称为第二类正发展速度,说明企业在基期与报告期都亏损。此时,仍定义: 增长速度=发展速度-1
四、运行的速度分析
在下面的速度分析中,以环比速度为标准,对经济运行进行分类考察,共有三种运行方式:
(一) 恒量运行
见前,此时发展速度恒为1。
(二) 匀发展速度运行
一个经济时间数列,如果它的环比发展速度为正且相等,这种运行就叫做经济的匀发展速度运行,简称匀发展洈速度运行(从数学角度看,此时构成一等比数列)。即:
ai+1
q=── (i=0,1,…,n-1)
ai
或 aj=aiqj-i (i,j=0,1,…,n-1) (9)
此时环比发展速度q为一正常数。累计和S的公式可写为:
a0(qn-1)
S=──── 当q≠1时
q-1
S=na0 当q=1时
十分明显,恒量运行就是发展速度为1的匀发展速度运行,是后者的特殊情形。
在公式(9)中,令j=n-1,i=0,则可得:
n-1─an-1
q= ── (10)
a0
这就是“水平法”平均发展速度的公式。但明显的是:从方法论的角度看,它仅仅适用于匀发展速度运行。而匀发展速度运行的平均发展速度就等于环比发展速度,因此,此时没有必要专门讨论其平均发展速度。当然,对于人口(这种具有数学意义上的马尔可夫性──Markov)时间数列,由于往往侧重于考察期未水平,则可例外。
(三) 变发展速度运行
一个经济时间数列,如果它的环比发展速度不相等或相等且为负,这种运行就叫做经济的变发展速度运行,简称变发展速度运行。经济的匀发展速度运行,同样是对现实经济运行的理想化抽象,在经济生活中一般是不存在。现实经济生活中,大量的、最为普遍的是变发展速度运行。对于这种运行方式,如何说明在一定时期内每期平均发展变化呢?假设从 a0到an-1有平均发展速度x,则x满足下列方程: 大家知道,即使对于一个正时间数列,如何简捷、可行地求解它所形成的高次方程(11),都一直成为各国数学家、经济统计学家研究和急待解决的重大难题;更何况现在取消了时间数列为正的限制,其困难将成倍的增加。令人欣喜的是,经过一年多艰辛的探索与努力,笔者已构造出一整套系统解决上述难题的计算技术,并研制出同累计平均增长量相配套可供实际大规模应用的计算机程序。由于笔者准备提供应用软件而不是计算技术,所以在此省略极其复杂的中间过程,仅给出关键性的结论。
定义:一个经济时间数列a0,…,an-1,假设a0≠0。
⒈如果∑ai/a0>0, 则称经济时间数列从a0到an-1是同向性的;并且a0>0,称做第一类同向性;a0<0时,称做第二类同向性。相应地分别存在着第一类、第二类正(累计)平均发展速度(其经济涵义参见发展速度,后同)。
⒉如果∑ai/a0=0, 则称经济时间数列从a0到an-1处于临界态;并且a0>0,称做第一类(或盈亏)临界态;a0<0时,称做第二类(或亏盈)临界态。相应地分别存在着第一类、第二类零(累计)平均发展速度。
⒊如果∑ai/a0<0, 则称经济时间数列从a0到an-1是异向性的;并且a0>0时,称做第一类异向性;a0<0时,称做第二类异向性。(当n为奇数时,需满足一定条件下)相应地分别存在着第一类、第二类负(累计)平均发展速度。
十分明显,这种累计平均发展速度计算方法的实质,是要求各年根据 x所推算的累计总和与各年实际所具有的水平总和相一致。
五、动态分析的一些原则
在动态分析中,过去由于采用了“水平法”平均增长量和平均发展速度,导致所推算的累计总和不相等,与实际水平总和也不相等。所以,往往只进行速度分析,而不进行增长量分析和实证分析。然而现在,随着累计平均指标的应用,这些问题与矛盾都将迎刃而解。为了体现动态分析是增长量分析与速度分析的统一有机体,是一种定量化的实证分析方法;同时,也是为了更加完整地说明经济发展变化情况,
结合原有的动态分析理论,明确提出下列一些动态分析的原则。
⒈序时平均数原则:在动态分析中,一般应该给出这一时期的序时平均数,以说明经济的平均发展水平。
⒉增长量原则:一般应该给出这一时期的累计平均增长量,以说明每期平均增长的数量。
⒊基期选择原则:应用累计平均指标,在很大程度上减弱了建立在两根支柱之上的“水平法”的不足,但并没有(也无法彻底)摆脱易受不同的参照基准──基期影响的缺陷。为了更加真实、准确地考察经济发展情况,归纳出以下一些基期原则。
(1) 原则:在动态分析中,有时以特定的时间的经济量做为基期来进行分析,把这种选择方式称为基期的政治原则。例如,以1945年的经济量为基期来考查二战后世界经济发展情况。
(2) 侏儒原则:以某一历史时期中的经济量处于“底谷点”的年份为基期,来考查经济发展情况,从而“跨大”了经济发展速度和增长量。
(3) 中庸原则:以某一历史时期中的经济量处于中间水平的年份为基期,以便比较“公正”地考查经济发展情况。
(4) 巨人原则:以某一历史时期中的经济量处于“高峰点”的年份为基期来考查经济发展情况,从而“降低”了经济发展速度和增长量。
(5) 平均值原则:在对不同经济指标,或对不同、地区、部门、国家同一时期的经济发展情况进行考查时,由于它们可能处于上述不同的基期原则,所以往往把连续三年或五年的简单算术平均数看做是中间一年的值,并以此值为基期,以便比较“公正”地对上述相应指标的发展情况进行考查(由累计法易知,此时不包括基期值推算的累计和等于实际累计和)。
⒋项数的偶数原则:在动态分析中,规定把异向性时间数列考察期的项数取为偶数,以确保此时累计平均发展速度的存在,从而进行速度分析。
六、一些结论
通过以上问题的提出、分类、定义、推导求解、以及计算机软件、实际应用结果和论述,笔者希望可以
得到下述结论:
⒈已建立了一套更加普遍和适用的动态分析的理论框架:在理论上对经济运行进行了分类;界定了累计平均增长量,矢量发展速度;并且系统、简捷、可行地解决了适用于同向性、临界态和异向性时间数列的累计平均增长量、累计平均发展速度的计算问题。
⒉用累计平均增长量和累计平均发展速度所推算的累计总和相等,且等于实际(水平总和),这就消除了用“水平法”平均增长量和平均发展速度计算的累计总和与实际水平总和之间的差额,使它们有机地统一起来,从而体现出经济分析的实证原则和起始于亚当·斯密时代的国民财富的积累原则。
⒊经济的恒量运行、匀增长量运行、匀发展速度运行,都是一种理想状态下的经济运行方式;而现实经济生活则是变增长量运行、变发展速度运行。如果我们忽视现实经济生活的特征,无视过程的变化而进行分析考察,虽然达到了计算、分析简化的目的,但可能使我们陷入偏离现实的危险;而用偏离现实的分析做基础来指导现实经济生活,将使我们离生活更远!
⒋从实际结果看,我们已运用所编制的程序分别计算了、甘肃省的15项经济指标的累计平均指标,均获得成功。笔者相信并希望:已给出的方法和编制的程序适用于任何时间数列,在国民经济计划、统计工作中,将会得到广泛的应用。从而结束没有累计平均增长量指标的历史,彻底改变有累计平均发展/增长速度指标,但在经济统计资料中又见不到的现状,以便更加准确、真实地研究、分析、考察和指导现实经济生活。
不论上述观点将会得到赞同或是反对,我们都必须指出这样一个事实──误差的马太效应原理:“水平法”同“累计法”平均指标任何差距,都将导致累计和的误差转入几何倍数增加或幂函数增加的局面,因此,当代的动态分析理论,应该放弃对现实经济生活简单性假设,抛弃对“水平法”过多的幻想,针对现实经济复杂性的特征,引入新的有益的概念和方法,来开拓一个建立在现实经济生活基础上的“累计法”时代!