关于经济学的一些设想：从劳动价值论到效用价值论

　　一、对劳动的一种深入认识，劳动在个体的累积效应
　　
　　
　　假设一社会只有两个劳动者甲、乙生产一种产品，两人不加任何区别。W是甲乙两人均要求的劳动最低支付曲线，Q是产品的产量，t是劳动时间，BC是现有的劳动生产率。A是一种发明创新的突破，它是某人对现有的生产与技术的掌握与熟练达到一定程度的结果，使得生产率有显著增长。如果没有A，两人的最优支付为E，而现在最优的是，对甲支付D，对乙支付A(设CD=AB)，或者二人互换，且要求完成相应的劳动时间。通过这个例子想要说明的是，科技进程中的大多数发明与创新是个人的经历，知识与思维的高度凝结，绝不可能分摊给多人完成，且对于个人是具有成本的，但也是可以替代的。
　　
　　再引入学习效应，假定一项事业可以分成均等的K份加以管理，管理对象只有好坏两种状态，处于好的状态的概率为。，且有很多个相同的管理项目和管理者，管理的需求与供给双方都是完全竞争的(不考虑多层级)。W＝kⁿ(k_-1+1)^1-n[ax+c-b(k_-1+1]n，a，b＞0，W是每个管理者在相应条件下要求的最低支付，k是本轮管理的规模(用份数表示)，k-1是上一轮管理的规模(设k＞k-1，k＜或=k，当k-1=k时，W=K(ax+c-bK)，D是这项管理的需求曲线，S(∑W)是供给曲线。n，a，b的取值在一适当的区间内，可以推知的情况是，这项事业最初是交由K个人管理，最终是由一人管理，∑W_终=KnK1－n(ax+c－bK)=K(ac+c-bK)较∑W_初＝k(ax=c-b)降低了。
　　
　　二、社会生产的结构
　　
　　花费在生产资料上的社会劳动时间总是有一个存量，它随着生产规模的扩大和科技的新旧更替不断增长，所增加的部分为生产资料存量的增加量。比如，一批投入生产的机器，假定生产规模一直不变，这批机器的数量由于机器的有形折旧一直不断被新投入使用的完全相同的机器弥补而保持不变，可以预见到某一天，由于科技的进步，这批机器由于精神折旧使得其价值几乎为0，不再用于生产，当这批机器全部被回炉炼回钢铁再生产出新式的机器，原来生产这批机器的社会劳动时间因此永远被固存了，而花费在新式机器上的社会劳动时间也成为了新的生产资料存量的增量。
　　
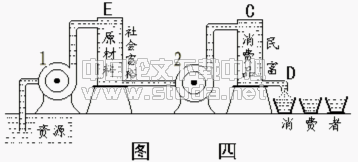
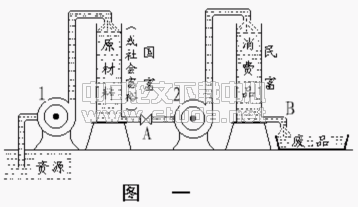
　　将生产资料存量的增加量与最终产品和服务作为最终产出，而将生产过程中所有用于购买最终产出的支付视为最终支付，将生产维持社会所需的生产规模而需弥补生产资料的有形折旧的部分看作生产相关产出的上部阶段，将销售也纳入生产进程作为生产的下部阶段，可以将社会生产简单地描绘如图。
　　
　　三、“立体”而非“平面”的交易支付
　　
　　
　　假设某种最终产出的生产过程自上而下地分成5个阶段，每个阶段由对最终产出的增值表示，如图。可知连续的生产进程中，除第一阶段外每个阶段都必须先将上一阶段的产品以前面全部阶段的增值量买下，这种购买部分上可以是以商业信用赊购赊销的形式，完成增值后再向下传递；各阶段的产品销售的资金回流与最终支付也会存在负的时间差，也就是说各阶段还要先买下本阶段的部分增值；这样最终产出的价值就被重复核算，所以由于社会分工十分复杂，要完成这个生产进程每个阶段就必须有一笔与最终产出价格和生产规模相适应的货币沉淀下来。无论是用于购买生产资料增量的资金和各阶段的营运资金的价值补偿，还是赊购赊销中的商业信用或直接或间接地都是以生产要素未来对各阶段部分增值的索取权为担保的，这里的生产要素一般是指资本或土地。

　　在货币M₁框架下的一种理想情形。续上，再假设：(1)生产进程中的各阶段开始时在银行中刚好有足够的存款能保证各阶段相应开出的支票足额兑现；(2)生产各阶段的购买完全垫支，各阶段必须将前面阶段和本阶段的所有增值买下才能生产出产品；(3)最终支付全部以现金的形式流通，所有交易支付都是同步一致的；(4)各阶段的自有资金、债券融资和银行贷款的比例相对不变，稳定。存在以下的循环：最初，每个．阶段持有用于购买本阶段增值的现金并开出与前面所有阶段值总额相等的支票用于购买上一阶段的产品，比如，第4阶段持有购买第4阶段增值的现金并且开出与第1、2、3阶段增值总额相等的支票，购买发生后，前一阶段收到这笔支票，将与此阶段增值额相等的部分兑换为现金持有而将剩余部分作为在银行的存款划归其账户，比如第3阶段收到第4阶段的支票后，将与第3阶段增值额相等的支票兑现而将与第1、2阶段增值总额相等的支票作为第3阶段的存款继续存在银行，同时，生产进程中最下端的阶段将最终产出售出获得总额与所有阶段的增值总额相等的现金，将与以前阶段的增值总额相等的现金存入银行，剩余现金继续持有，从而完成循环，两类货币回归平衡，比如第5阶段将最终产出售出后获得与第1、2、3、4、5阶段增值总额相等的现金，之后将与第1、2、3、4阶段的增值总额相等的现金存入银行，而继续持有与第5阶段增值额相等的现金，回到最初的情形。因此，经济若要保持稳定，银行的存款准备，以最终支付形式存在的现金，生产进程中沉淀的现金和支票存款都需要同时保持一定比例，利率起着很重要的调节作用，同时这还需要一个完善的银行体系。
　　
　　四、萨伊分配理论的解析，资本与土地索取权背后隐含的劳动求偿
　　
　　Tx、Ty为生产最终产出X、y的社会必要劳动时间，比较两式的结构可知，P与T具有相同的经济学意义，都是表示资源对产出的约束，但在生产关系的层次上来说，人的劳动(贡献)才是对产出的唯一约束。
　　假设存在一组私人劳动转化为社会劳动的系数　(可参鉴第五小节)，由此社会必要劳动时间，而任何一个经济参与者从最终产出中获得的效用相互之间实际上是不能也是不用比较的，单独构成上面各自的数量方程关系，从而一般均衡可以建立在下面一个假定的基础上。每个人按照自己的意愿将自己的劳动投入生产并且以科技水平允许的最优生产率生产出需要的每种产品的数量满足自身消费，达到各自的效用最大化，社会分工和交易不过是为了实现这样一组最优的生产率而已。
　　实际上资源对产出是有限制的，这样就有了对固定
量的生产要素支付问题。
　　
　　如果最终产出x的生产中必须要某种生产要素M，M的数量相对于人的劳动是稀缺的，这样就使得上述系列方程组不再成立，为了配平这一系列方程组，在关于x的项的分母下面全部添加T_X，M，使得所有人对x的总消费量等于总产出量，T_X，M就变成了是同人的劳动贡献并列相当的对固定生产要素按其“贡献”的索取权支付，如地租。但实际上并非一定如此，比如，在x没有生产之前，某人发明创新了生产x所必需而且仅缺的一项技术，假定此时M的价值为0，技术的发明创新者将M的所有权以代价0买下，并将技术投入生产出x，则可以通过固定要素按其“贡献”的索取权或是以由此形成的公估价值将M(附加技术)卖出获得发明创新这项技术的劳动补偿；同样，一个生产x的生产要素"的持有者直接向发明创新者支付1买下技术投入生产或是由生产要素M的持有者借给发明创新者一笔资金以公估价值n将生产要素M买下，由他将技术投入生产，待生产要素M(附加技术)升值后，再以公估价值m卖还给原生产要素的持有者，在公平交易和不考虑其他因素的条件下，两种情况等价，可知1＝m-n，实际的收入分配由市场、经济条件决定。
　　资本可以看作一种半固定量的生产要素，在短期资本是“稀缺”的，但在长期当资本的“贡献”所隐含的人的贡献(劳动)得以补偿，由于竞争，资本自由流人生产进程得以“充足”，生产得以充分调整，理想条件下，已投入生产进程的资本的租金TK趋向于0。但竞争过程取决于许多因素，并不是完全的约束机制，发明创新中包含的劳动决定着竞争力的大小和仿制的难易程度，但产生的收益可能是远远大于公平的劳动补偿或是说潜在的最优支付。而且发明创新的普及存在阻碍时(有时是纯粹的垄断)产生的收益是在其所有的产生要素持有者之间进行分割的。再有，如果因为经济波动等生产中的资金耗损要以一定的市场利率引入新的资金时，就会保留相当的实际利润率，同时也保证了生产中的资金不会流出。而随着科技的发展越来越快，需要新的理念和思维，新的商品生产者取代旧的生产者的速度也会越来越快。