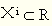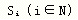经济学分支介绍(11)——数理经济学
数理学是运用数学方法对经济学理论进行陈述和研究的一个分支学科。在经济史上把从事这样研究的人叫做数理经济学家,并且归为数理经济学派,简称数派。
西方第一个把数学用于经济问题的是意大利的切瓦,他于1711年写了一本关于货币价值的书。但首先比较系统地运用数学的,是1838年法国库尔诺的《财富理论数学原理的研究》,这书常被当做数理经济学的开端。
由于当时的经济理论权威们不熟悉数学推理,而无人问津,直到40年后因受到英国的杰文斯和法国的瓦尔拉斯的高度推崇,才知名于世,并被当做数理经济学和数理学派的正式起源。此后英国的埃奇沃思、马歇尔、美国的费希尔、意大利的帕累托等进一步了数理经济学。
库尔诺并没有用过“数理经济学”的名称,他采用的书名用意不仅在于理论研究,而且在研究中要运用数学分析的形式和符号。他认为在财富理论中运用数学分析 ,是为了探索不能用数字表现的数量之间的关系,和不能用代数表现的函数之间的关系;即使不需要精确数字,只要能更简明地陈述问题、开辟研究途径、避免脱离主题,数学也有其有用之处,如果仅仅因为不熟悉或怕用错而拒绝数学分析,是荒谬的。
杰文斯1862年发表的《略论经济学的一般数学理论》是数理经济学的最早名称,到1879年他的主要著作《政治经济学理论》一书再版时,附上1711年以来的“数学的经济的”目录,等于公开宣称数理经济学的存在。他认为经济学要成为一门,必须是一门依赖于数学的科学,简单原因就是研究数量和数量之间的复杂关系,必须进行数学推理,即使不用代数符号,也不会减少这门科学的数学性质。
杰文斯的目的是要为价值的最终理论以及建立在这个理论之上的市场提供数学解说。他的理论中心是“价值完全由效用决定”。他把商品对所有者的效用分为总效用和最后程度的效用(即后来的边际效用),后者是商品拥有或消费总量增加时,总效用增加量对商品增加量的比率。
他认为随着商品拥有量的增加。最后程度的效用会逐渐降低,并据此用数学方法推出:一种商品所有者和另一种商品所有者互相交换商品可以增加总效用,交换要进行到两种商品的最后程度效用相等、总效用最大达到均衡时才停止,这时两种商品在两个所有者之间的交换比率应该等于交换完成后两种商品的最后程度效用的反比。
瓦尔拉斯在1874年出版的《纯粹学纲要》一书中认为,纯粹经济学实质上就是在假设完全自由竞争制度下,关于价格决定的理论;价格存在是因为商品具有数量有限和有用的条件,只要有交换就会有交换价值。
交换价值是个可计量的数量,正是一般数学的研究对象,所以交换价值的理论应该是数学的一个分支;数学方法并不是实验方法而是推理方法,经济学的纯粹理论也象“物理-数学的”一样,从经验的真实概念中抽象出理想的概念作为基础,可以超出经验范围进行推理,在建成这个科学后再回到实际,也不是为了验证,而是为了应用。
瓦尔拉斯的主要理论是建立在边际效用价值论之上的一般均衡理论体系。库尔诺虽然也考虑过个别商品的产、销、进出口对其他商品生产者的收入会产生反作用,但仍然限于局部分析,没有同时照顾全局,瓦尔拉斯企图用数学方法加以补救。
埃奇沃思最早研究商品各种议价的经济后果,并且提出无差异曲线的概念以便避免用货币作为计量边际效用的固定单位,后经帕累托改进,用以代替边际效用,作为一般均衡的理论基础。马歇尔的理论核心是认为一种商品的均衡价格就是在其他情况不变时,该商品的需求价格与供给价格达到一致时的价格,所以又称为局部均衡论。
数学在经济理论中的应用越来越广泛,一方面运用数学方法研究的理论领域还在扩大;另一方面,对前人研究过的问题还不断运用更深奥的数学方法进行更深入的探讨。
20世纪60年代以后,数理经济学和微积分、集合论、线性模型结合在一起,同时数学方法的运用几乎遍及经济学的每个领域。经济生活的需要和机的发明,促使与数理经济学有关的经济计量学得到迅速,它反过来又推动数理经济学继续前进。
利用数学方法研究经济问题,有利于发现经济问题的实质,指明经济问题的发展、变化的趋势。现在研究经济问题时,进行数学分析已经是不可或缺的方面,任何脱离了数学的经济问题分析都会被认为是不可靠的。随着人们对经济活动认识的深入,数理经济学也在不断的发展、完善。