顶部自由、底部嵌固桩计入自重的屈曲分析

摘要：本文采用弹性地基反力理论，利用能量法导得了桩顶自由、桩端嵌固条件下，基桩计入自重影响后屈曲问题的稳定方程，并给出了方程的解答和基桩稳定长度随桩的入土深度的关系曲线，可以用于工程实用。本文计算结果表明：一般情况下，基桩自重对基桩屈曲分析的影响较小，可忽略不计。
　　关键词：基桩； 能量法； 临界荷载； 自重
　　
　　1前言
　　
　　随着细长桩和高桩在工程中的广泛应用，竖向荷载作用下基桩的屈曲分析（稳定性分析）具有重要的实际工程意义并逐渐为人们所重视。与一般杆件的屈曲分析不同，基桩在竖向荷载及桩周土体的约束下，其稳定性分析极为复杂，国内外已有不少研究，如Davisson（1963）等的模拟计算机解[1]，Poulos（1980）的弹性理论解[2]，Bowles的有限单元解[3]等。[4]、[5]在综合我国大量工程应用经验的基础上，给出了根据基桩两端约束条件、桩侧土性质和基桩入土深度情况确定基桩稳定计算长度的简便公式，但缺乏严格的理论依据和准确的试验验证。文献[6]~[8]从最小势能原理出发，导出了求解基桩临界荷载及稳定计算长度的计算公式，其研究结果表明：基桩桩侧摩阻力对其稳定性的影响甚微，在分析时可忽略不计。
　　稳定计算理论表明，在进行稳定分析时，结构自重的影响不宜忽视[9]。而在传统的基桩屈曲分析中，通常套用杆系结构稳定分析方法[10]、[11]，显然，由于忽视了桩侧土的约束作用，将使计算值偏小。同时，以往的基桩屈曲分析没有考虑基桩自重的影响。为精确分析基桩自重对临界荷载和稳定计算长度的影响，本文采用能量法对计入桩身自重作用的桩顶自由、桩端嵌固桩的竖向稳定性进行了研究。本文研究方法对其它约束条件下基桩的屈曲分析同样适用。
　　
　　2分析模型及计算公式
　　
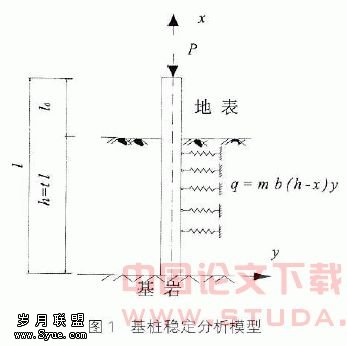
　　在竖向荷载作用下，基桩桩顶自由、桩端嵌固时，其稳定分析模型如图1所示。设桩身自重沿桩深度呈线性变化，并将其化为线荷载g(x)，其计算公式为：
　　

　　(1)当桩长及入土深度一定时，随着自重无量纲影响系数 的增加，桩的无量纲稳定长度 将增加。
　　(2)一般情况下，桩的自重作用对其稳定性的影响甚小。但随着的减小和 的增大，桩的自重作用对其稳定性的影响将不可忽略。
　　
　　4算例 
　　 顶部自由、底部嵌固的圆形混凝土桩，直径D=0.3m，桩长L=20m，桩侧土的水平抗力系数的比例系数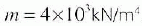，不考虑桩侧摩阻力影响，试用本文方法求其入土深度分别为h=15m、h=10m时的稳定计算长度和临界荷载，并将其与不计自重时的结果进行比较。
　 　

         
　　
　　5结语
　　
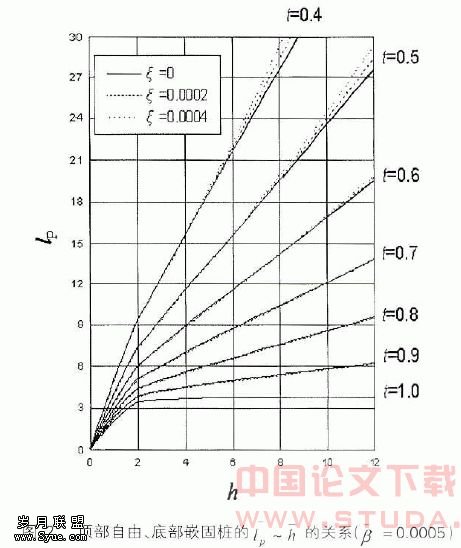
　　5.1本文利用能量法原理，导得了基桩计入自重时的屈曲问题的稳定方程，利用数值方法对该方程进行了求解，并给出了基桩稳定计算长度随桩的入土深度的关系曲线，可以用于工程实用。
　　5.2计算结果表明，一般情况下，基桩自重对基桩屈曲分析的影响较小。
　　5.3当桩的自由长度较大、入土深度较小，且桩周地基土质较软弱时，基桩自重的影响较大，不可忽略。
　　
　　：
　　[1] Davisson,M.T. and Robinson,K.E.,“Bending and Buckling Pratially Embedded Piles.”Proc.6th ICSMFE vol.2, 1965.
　　[2] Poulos, H.G. and Davis, E.H.,Pile Foundation Analysis and Design, New York: Willy, 1980.
　　[3] Bowlos, J.E.编著，唐念慈等译.基础工程分析与设计.北京：建筑出版社，1987.
　　[4] 建设部部标准.建筑桩基技术规范（JGJ94-94）. 北京：中国建筑工业出版社，1995.
　　[5] 部部标准.公路桥涵与基础设计规范（JTJ024
　　-85）. 北京：人民交通出版社，1995.
　　[6] 赵明华.桥梁桩基的屈曲分析及试验.中国公路学报，1990,3(4)：47~56.
　　[7] 赵明华，王季柏.基桩计入摩阻力的屈曲分析.岩土工程学报 ，1996,18(3)：87~90.
　　[8] 杨维好，宋雷.顶部自由、底部嵌固桩的稳定性分析.工程力学，2000,17(5)：63~66.
　　[9] 刘光栋，罗汉泉.杆系结构稳定.北京：人民交通出版社，1988.9.
　　[10] 赵明华.桥梁桩基计算与检测.北京：人民交通出版社，2000.1.
　　[11] 胡人礼编.桥梁桩基础分析和设计.北京：中国铁道出版社，1987.
　　[12] 孙训方，方孝淑，关来泰.材料力学（第二版）.北京：高等出版社，1987.
　　[13] 同济大学计算数学教研室编.数值分析基础.上海：同济大学出版社，1998.