基于灰色系统理论的室内空气品质的评价方法
来源:岁月联盟
作者:佚名
时间:2010-08-24
3.2 评价实例
以表3所示的室内空气品质实测值[1]进行等级评价和优劣排序。
四栋大楼的室内空气品质实测值 表3  | 1栋 | 2栋 | 3栋 | 4栋 | | 二氧化碳(ppm) | 721.9 | 854.4 | 740.7 | 953.6 | | 一氧化碳(ppm) | 1.97 | 3.40 | 1.90 | 3.51 | | 吸入尘(mg/m3) | 0.105 | 0.089 | 0.054 | 0.051 | | 菌落(CFU/9cm·5min) | 4.8 | 5.1 | 5.79 | 3.52 | | 甲醛(ppb) | 36.9 | 72.9 | 65.7 | 80.7 | | 二氧化氮(mg/m3) | 0.0084 | 0.039 | 0.024 | 0.031 | | 二氧化硫(mg/m3) | 0.0122 | 0.0145 | 0.0127 | 0.0132 |
3.2.1原始序列的预处理
如前所述,在灰色评价中各原始序列含有不同物理量,它们量纲不同,在数值上也相关较大,应进行预处理,使原始序列中各元素成为数值上相关不大的无量纲值。
由韦伯-费希纳定律:R=klogS,可知反应的大小与刺激量的对数成正比,因此我们可对各污染物浓度的数值进行处理,使之能反映人体感觉的大小,且能在不同的污染物之间进行比较。依照噪声单位分贝的定义,提出如下式[9]:
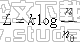 (7) (7)
式中:n----实测的浓度值;
n0----作为比较的浓度值;
我们将n0取各污染物的背景值,并且将清洁级别的计算值取为0,轻污染级别的计算值取为2,这样就可得到对应污染物的k值。
我们采用式(7)对原始序列进行处理,得到如表4、5所示的预处理后的评价序列。
无量钢化处理后的室内空气品质评价标准序列 表4  | 清洁 | 未污染 | 轻污染 | 重污染 | | 二氧化碳 | 0 | 1.06 | 2 | 3.28 | | 一氧化碳 | 0 | 1.16 | 2 | 2.97 | | 吸入尘 | 0 | 1.23 | 2 | 2.95 | | 菌落 | 0 | 1.4 | 2 | 2.89 | | 甲醛 | 0 | 1.01 | 2 | 2.98 | | 二氧化氮 | 0 | 1.2 | 2 | 2.95 | | 二氧化硫 | 0 | 1.19 | 2 | 2.74 |
无量钢化处理后的室内空气品质实测值 表5 
| 1栋 | 2栋 | 3栋 | 4栋 | | 二氧化碳 | 1.289 | 1.657 | 1.345 | 1.896 | | 一氧化碳 | 0.287 | 0.863 | 0.249 | 0.892 | | 吸入尘 | 1.602 | 1.417 | 0.86 | 0.796 | | 菌落 | 0.347 | 0.392 | 0.486 | 0.118 | | 甲醛 | 0.761 | 1.607 | 1.478 | 1.734 | | 二氧化氮 | -0.151 | 1.182 | 0.76 | 0.983 | | 二氧化硫 | 0.147 | 0.274 | 0.177 | 0.205 |
3.2.2 计算过程与评价结果
在这个评价实例中M={1,2,3,4},N={1,2,3,4},L=={1,2,…7},取分辨系数ρ=0.5,由表4、5数据,根据公式(1)、(2)可求出:
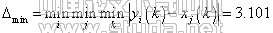
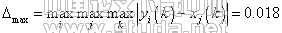
再根据式(3)、(4)、(5)依次求出关联系数、关联度,从而得到室内空气品质评价的关联矩阵R,为表达方便用表6表示如下:
室内空气品质评价的关联矩阵R 表6  | 清洁 | 未污染 | 轻污染 | 重污染 | 最大关联度对应的等级 | | 1栋 | 0.7507 | 0.7091 | 0.5594 | 0.4099 | 清洁 | | 2栋 | 0.6293 | 0.7802 | 0.6560 | 0.4598 | 未污染 | | 3栋 | 0.7056 | 0.7317 | 0.5807 | 0.4227 | 未污染 | | 4栋 | 0.6708 | 0.7228 | 0.6439 | 0.4491 | 未污染 |
根据关联矩阵,我们可得以如下结果:
(1)根据关联分析的基本原理,每一大楼最大关联度对应的级别即为其室内空气品质评价的结果,可见1栋属于清洁等级,2栋、3栋和4栋属于未污染等级。
(2)如上所述,关联矩阵的任意两个关联度值的比较是有意义的,它提供了关于评价对象的丰富信息。关联矩阵中任意两行的相应元素为相应的两个评价对象各自与某一等级的灰色关联系数,比较任意两行的相应元素的大小,可得取相应两个评价对象关于不同级别的关联程度比较。在品质优的等级,关联系数越大,品质越优;在品质劣的等级,关联系数越大,品质越差;在两个评价对象A、B的比较中,如果意味着A栋空气品质优于B栋的关联系数占多数,则说明A栋的空气品质比B栋好。
在本例中,只有1栋属于清洁级别,所在在四栋大楼中它的室内空气品质是最优的,另外比较同一列的各元素可知在清洁级别它的关联度是最大,在其它级别它的关联度是最小的,这也同样说明了1栋的室内空气品质是最优。虽然2栋、3栋和4栋都属于未污染级别,但通过分析关联矩阵仍能比较它们之间的优劣。比较矩阵第二、三、四行的相应元素,可知2栋关于清洁级别的关联度最小,关于其他三个级别的关联度都是最大,所以2栋的室内空气品质是最差的。同样地,我们比较第三、四行的相应元素,可得出3栋的室内空气品质优于4栋。综合上述分析,四栋大楼室内空气品质由优到劣的排列次序为:1栋、3栋、4栋、2栋。
4 分析与讨论
上述评价实例得出的结论与运用评价指数法、模糊综合评价法得出的结论基本相同,比较三种方法,可知:
评价指数法中的单因子评价指数表明了单个污染物对室内空气的污染程度,但不能获得各种评价因子共同作用的综合信息。综合评价指数能够反映多种污染物共同作用于室内空气的综合效应。在运用综合评价指数进行评价时,应先计算综合评价指数,再按指数大小划分等级,只要选择合适的综合评价指数,就能够较客观地评价室内空气品质的状况。
模糊综合评判法需要建立各因素对每一级别的隶属函数,过程较繁。而且其复合噎程的基本运算规则是取小取大,强调权值的作用,丢失信息较多,突出严重污染物的影响,而忽视了各项污染因子的综合效应,使污染水平和严重方向移动,在一定期程度上失去了综合评价的意义。
灰色关联分析方法计算过程简单方便,实测得到的所有数据对评价结果都有影响,充分利用了获得的信息。根据灰色关联矩阵提供的丰富信息,不仅可确定样本的级别,而且能反映处于同一级别样本之间的室空气品质差异,评价结果直观可靠。
由于目前仍没有提出系统的室内空气品质标准及等级分类,且对室内空气品质等级的划分还应和人群对室内空气品质的主观感受相联系,为使室内空气品质的等级划分及排序更具意义,还应根据对室内空气品质的主观调查结果,找出对主观感受有重大影响的污染物,对评价标准序列作出调整,使灰色评价既能反映室内空气品质客观现状,又能体现人们对室内空气的主观感受。
1 沈晋明,毛继传,孙光前,上海办公大楼空气品质客观评价,通风除尘,1995,15(4):14~17
2 初春玲,曹叔维,周俊彦,室内空气品质模糊性综合评判,通风除尘,1999,19(3):9~11
3 Preston E. McNall Indoor Air Quality. ASHRAE Journal, 1986 (6): 39~48.
4 沈晋明,室内污染物与空气品质评价,通风除尘,1995,15(4):10~13
5 邓聚龙,灰色控制系统,武汉:华中理工大学出版社,1992
6 刘思峰,郭天榜,党耀国等,灰色系统理论及其应用,北京:出版社,1999:40~41
7 曾光明,杨春平,卓利,环境系统灰色理论与方法,北京:科学技术出版社,1994:69~70
8 陆雍森,环境评价,上海:同济大学出版社,1990
9 M.V. Jold. Evaluation of indoor quality using the decibel concept based on carbon dioxide and TVOC, Building and Environment, 2000, Vol. 35: 677~697 |
| |
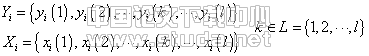
 (6)
(6)