主成分分析在空调系统传感器故障检测与诊断中的应用研究

　　空调系统中保证各类传感器的读数正确，及时发现传感器故障，是空调系统最估运行的重要保证。我们已经给出了空调系统的传感器故障类型^[1]，本文将用主成分分析法对空调系统中传感器的这些类型的故障进行诊断，以便及时辨别出故障类型，做出正确决策，及时恢复测量，使系统可靠正常运行。
　　
1 主成分分析法（PCA）及故障检测、识别方法
　　
　　某一系统或过程传感器测量值之间并不是孤立的，它们之间具有高度的相关性，在正常情况下，这种相关性是由物理、化学等基本所控制的，如：质量守恒、能量守恒等。而当某些传感器出现故障时，就会打破这种测量值之间的相关性。主成分分析法能充分反映这种相关性，因此，我们采用PCA方法进行故障检测与诊断。
　　
　　1.1 PCA建模
　　设某测量矩阵， ，其中m是测量变量数，n是测量样本数。X的每一列都进行了零平均化，X可以分解为：
　　 　　　　　　　　　　　　　　　　　　　 （1）
　　其中 ----测量的可模部分， ----测量的残差部分，在正常情况下，主要是自由噪声。
　　根据PCA的方法， 和 可分别表示为：
　　 　　 　　　　　　　　　　　　　　　　　　 （2）
　　　　 　　　　　　　　　　　　　　　　　　 （3）
　　式中：T----得分矩阵， ；
　　　　　P----荷载矩阵， 。
　　其中，l为PCA模型所包含的主成分数，后面将介绍如何确定它。P的列向量分别是X的协方差阵P的前l个最大特征值λ_i所对应的特征向量。 的例则分别是剩下的m-l个特征微量。根据统计学原理，X的协方差阵可以用下式进行估计：
　　　　 　　　　　　　　　　　 （4）
　　对于每一个测量样本x，其可表示成为：
　 　　　 　　　　　　　　　　　　　　　　　　 （5）
　　 　　 　　　　　　　　　　　　　　　 （6）
　　式中，
　　　　 　　　　　　　　　 （7）
　　 是x是在主成分子空间PCS（Principal Component Subspace）内的投影，而 是x在残差子空间RS（Residual Subspace）内的投影。
　　
　　1．2 故障检测
　　在正常情况下，测量样本向量在残差子空间内的投影应当很小，主要是自由噪声。当某一故障发生时，这个投影就会显著地增加。因此，可以通过检测测量数据在RS内的投影大小 来检测故障是否发生。通常使用的统计量是：平方预测误差SPE（Squared Prediction Error），如式（8）所示：
　　　　 　　　　　　　　　　　　　　 （8）
　　当 时，认为系统运行正常，而当 时，就认为系统出现故障。δ²为SPE的置信限。δ²可用下式^[2]。
　　　 　　　　　　　　　 （9）
　　　 　　　　　　　　　　　　　　　　　　　　　　 （10）
　　　 　　　　　　　　　　　　　　 （11）
　　式中：l----模型的主成分数；
　　　　　c_a----置信度为a的标准正态分布置信限；
　　　　　λ----协方差阵R的特征值。

　　1．3 故障重构
　　利用式（6），可以对故障向量x进行估计，也就是说， 可以看在是x的一个估计值。但是， 并不是x的最佳估计，因为在估计 时所使用的x是包含有故障的数据。因此，为了消除故障的影响，利用前一次获得的估计值x^new去代替x，通过多次近迭代，就会使得x^new逼近于x的正常值x*。
　　假设样本x中的第I个分量发生了故障（假设只有一个故障），即x_i是一个故障值，可以利用下式进行迭代：
　　　 　　　　　　　　　 （12）
　　式中， 为矩阵的C的第I列用0代替c_ii值之后的向量。可以证明，该迭代总是收敛于^[3]：
　　　　 　　　　　　　　　　　　　　　 （13）
　　式中，c_ii≠1，说明该变量不能被重构。

　　1.4　故障鉴别
　　为了进行故障鉴别，[4]提出了一种针对各种可能的故障方向，利用逐个重构的方法进行故障鉴别。对于测量值x，由于故障的存在，其SPE（x）必定会显著增加，若故障重构的方向正好是故障发生的方向，其重构后的SPE（）必定会显著地减少，若重构的方向不是故障发生的方向，则SPE（）不会发生显著地变化。因此，可以用鉴别指数SVI进行鉴别：
　　　　 　　　　　　　　　　　　　　　　　　 （14）
　　其中（）----是测量向量x沿第j个方向重构后的数据向量。
　　显然，SVI∈[0 1]，若SVI_j接近1，说明第j个重构方向不是故障发生的方向；相反，若SVI_j接近0，说明第j个重构方向正好是故障发生的方向。
　　
　　1．5 最优主成分数的确定
　　前面在建立模型时已经用到了主成分数的概念。主成分数对模型的好坏影响很大，如果主成分数选得过小，不利于小故障的检测；而若主成分数选得太大，又会不利于大故障的检测。因此，存在一个确定最优的主成分数的问题。可以根据不可重构的方差来选择最优主成分数^[4]。
　　不可重构方差是指重构前后测量变量之间的方差：
　　 　　　　　　　　　　 （15）
　　式中：Var（.）----表示方差算子；
　　　　　E（.）----表示数学期望算子；
　　　　 ----x_j的重构值；
　　　　　x_j----的第j个分量；
　　　　　ξ_j----为故障方向向量。
　　用保证最小总的不可重构方差来确定最优的主成分数，即：
　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （16）
　　这样，通过选择不同的主成分数l，分别计算出∑uj，最后选取最小的∑uj所对应的主成分数为最优的主成分数。
　　
2 传感器故障的检测与诊断的空调监测系统
　　
　　图1是一空调系统冷冻机房系统示意图。该系统包含两台同样的制冷机，每台制冷机配备有各自的一级水泵，为保证每台制冷机蒸发器冷冻水的流速基本不变，一级泵为定速泵。两台二级泵为建筑供水，二级泵根据建筑负荷大小变频调节水泵的供水量，多余的水量由旁通管流回制冷机。当旁通流量大于一台一级泵的流量时，停止一台制冷机及相应水泵；而当旁通流量出现负值且大于一定的时间时，开启一台制冷机及相应的一级泵。为保证制冷机的工作时间大致相等，实行先停先开、先开先停的控制策略。
　　系统的传感器的安装位置与类型如图1所示。共有四个流量传感器：制冷机1、制冷机2出口各有一台流量计，建筑供水流量计，旁通流量计。共有五个温度传感器：制冷机1、制冷机2供水温度传感器，建筑供水温度传感器，建筑回水温度传感器，制冷机回水温度传感器。
　　　　　
　　　　　　　　　　　　　　　　　　　图1 空调系统冷冻机房系统示意图
　　
　　根据给定的负荷，在HVAC专用仿真软件TRNSYS上对系统进行仿真。传感器的采样时间间隔为1min，仿真时间为4d。从采样的数据中选取稳定条件下的正常操作数据共5000组，进行平均化后，且前述方法建立模型。

3 故障诊断
　　
　　首先确定主成分数。不同的主成分数时总的不可重构方差，选取决的不可重构方差最小时的主成分数为最优主成分
数。此时的最优的主成分数是3，因此用3个主成分建立模型。
　　为了比较四种类型故障，选用同一个传感器----建筑供水温度传感器进行故障检测和诊断，随机误差 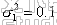。无任何故障时的测量信号见图2（a），正常条件下的故障检测情况见图2（b）。从图中可以看出，SPE（x）没有超出极限值δ²，说明数据正常。
　　　　　　　　
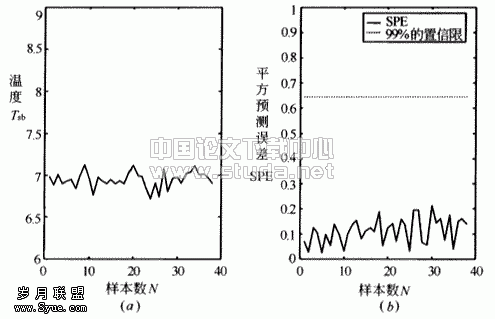
　　　　　　　　　　　　　　　　　　　　　　　　　图2 正常数据的检测
　　　　　　　　　　　　　　　（a）正常建筑供水温度数据信号；（b）正常数据的检测结果
　　
　　3.1 偏差故障
　　选ft=1.5℃，由[1]式（3）计算了出这时的故障测量值。图3（a）是这时的正常数据与故障数据的比较。图3（b）是这时的故障数据检测结果，SPE值超过了δ²限，检测出故障。SVI指数监测结果见图3（c）。
　　
　　3．2 漂移故障
　　选取d=0.05，由文献[1]式（5）计算出这时的故障测量值。图4（a）是这时的正常数据与故障数据的比较。图4（b）是这时的故障数据检测结果，在故障发生一段时间后，SPE值超过了δ²限，检测出故障。SVI指数监测结果见图4（c）。由图可以看出，由于故障大小是逐渐增加的，在刚开始，故障很小，不能被检测出。随着时间的推移，故障不断增大，SPE指数也不断在增加，故障被检测出来。
　　　　　　　　　　　　　　　　
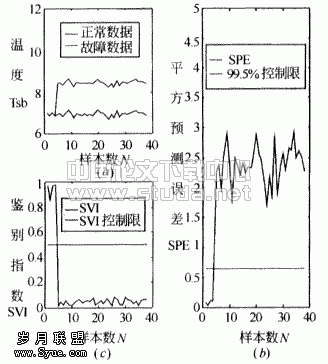
　　　　　　　　　　　　　　　　　　　　　　　　　图3 偏差故障检测与诊断
　　　　　　　　　　　　　　
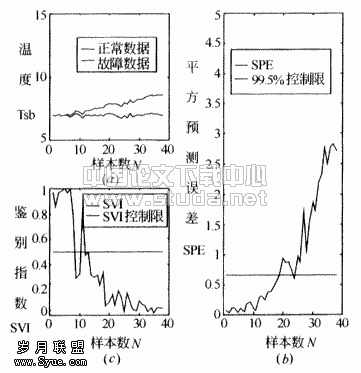
　　　　　　　　　　　　　　　　　　　　　　　　图4 漂移故障检测与诊断
　　　　　　　　　　　　　　（c）正常数据与故障数据比较；（b）故障检测；（c）故障鉴别
　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　图5 精度等级下降的检测与诊断
　　　　　　　　　　　　　　　　
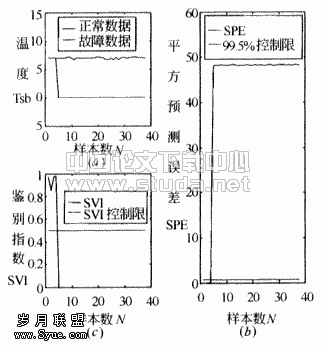
　　　　　　　　　　　　　　　　　　　　　　　　　图6 完全故障检测与诊断
　　　　　　　　　　　　　　　（c）正常数据与故障数据比较；（b）故障检测；（c）故障鉴别
　　
　　3．3 精度等级下降
　　选取ft∽N（0,2），由文献[1]式（7）计算出这时的故障测量值。图5（a）是这时的正常数据与故障数据的比较。图5（b）是这时的故障数据检测结果，图5（c）是SVI指数监控结果。从图中可以看出，SPE指数的波动很大，有时很大，而有时又很小，甚至不能被检测到，但多数情况超过了极限。这主要是由于故障类似于噪声的原因造成的。SVI指数也是如此。因此，对于这类故障，如果 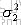较小时，很容易被人认为是自由噪声而难于被检测出.
　　
　　3.4 完全故障
　　选取x_t=0℃，图6（a）是这时的正常数据与故障数据的比较。图6（b）是这时的故障数据检测结果，SPE值远远超过了δ²限，指数很大，说明这时的故障较大。完全故障与偏差故障表现很相似，但完全故障的SPE远偏差故障大。
　　
4 结语
　　
　　本文利用主成分分析法对空调系统传感器四种故障进行诊断。SPE指数和SVI指数分别用来进行故障检测和鉴别。通过最小化总体不可重构方差来确定模型的最优主成分数。对空调冷水机组监测系统传感器的四种类型故障检测与诊断特性进行了比较，主成分分析法是一种很好的传感器故障检测方法，对传感器的各类故障均有很好的检测、诊断特性。
　　
　　
文献
　　
　　1 陈友明，郝小礼，空调系统中传感器故障检测与诊断方法的研究----传感器的故障类型及数学描述，全国暖通空调制冷2002年学术年会集，2002，11
　　2 J. Edward Jackson, Govind S. Mudholkar. Control Procedures for Residual Associated with Principal Component Analysis. Technometrics, 1979, 21 （3）:341～349
　　3 Ricardo Dunia, S. Joe Qin, Thomas F. Edger, Thomas J. McAvoy. Identification of Faulty Sensors Using Principal Component Analysis. AICHE Journal, 1996, 42 （10）:2797～2812.
　　4 S. Joe Qin, Ricardo Dunia. Determining the Number of Principal Components for Best Reconstruction. Proc. I-FAC Dynamic and Control of Process Systems, 1998: 357～362