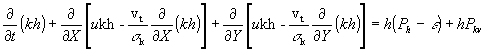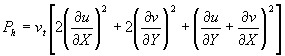空腔回流区水沙特性的计算分析
摘要:建立了回流区水深平均平面二维水流泥沙数学模型,提出了平衡输沙模式下回流区泥沙淤积方法;采用长江院空腔回流泥沙淤积水槽试验数据,验证了回流区泥沙淤积计算方法的可行性和精度;通过数模计算分析,一方面加深了空腔回流区环流结构及含沙量分布的机理认识,另一方面研究了模型变率对回流区水沙特性的影响。
关键词:空腔回流区 二维水沙数模 环流结构
1概述
河道水流由纵向水流(主流)和次生流(副流)构成。当次生流与纵向水流结合在一起时,将形成螺旋流,弯道水流属于典型的螺旋流;当次生流基本上脱离纵向水流形成相对封闭的环流时,即产生了回流。回流流动形态上的封闭性是相对的,回流区内的水流与泥沙仍然与纵向主流区的水流和泥沙不断地进行着质量、动量及能量的交换,这种交换主要是通过回流区交界面(即紊动掺混区)进行的;回流区水流及泥沙的运动呈现出强烈的三维运动特性,如:竖轴环流(天然河道中最为常见的回流形态)不仅存在着平面上的环流运动,还存在着上下层水流和泥沙之间的强烈掺混;挟沙水流河道或水槽中的回流区既可能发生泥沙冲刷,也可能出现泥沙淤积,这主要取决于回流区环流强度、河床组成以及纵向水流含沙量等因素,天然河道中的回流区以泥沙淤积为主[3~5]。
回流区环流和泥沙淤积特性的研究不仅具有理论意义,而且对于三峡工程泥沙问题的研究具有实际应用价值。三峡水库变动回水区河段呈现出宽窄相间、浅滩交错的河道形态,存在着许多港池回流区,如青岩子河段的沙湾,丝瓜碛河段的五羊背,铜锣峡河段的郭家沱、唐家沱和明月沱等;盲肠河段或渠段口门回流区的泥沙淤积也是三峡工程重要泥沙问题之一,已建的葛洲坝工程三江上下游引航道以及在建的三峡工程五级船闸引航道均存在着口门回流泥沙淤积及对策研究问题;两江汇合和分汊河道汇流区也会产生小及强度不等的回流区,它们对于河口拦门沙的形成及分汊河道的演变等具有重要作用;较为典型的回流区还包括汛期泄洪时坝前电厂两侧回流,丁坝、围滩及取排水口等工程局部区域回流等。
采用数学模型模拟回流区环流和计算回流区泥沙淤积是一种有效的方法之一。对于枢纽及河道泥沙实体模型,一方面模型设计以重力相似作为水流动力相似的首要条件,而让水流紊动粘性的相似产生偏离;另一方面部分模型采用了变态模型(特别是水库变动回水区模型和河口模型);加之,模型比尺一般较小,水流和泥沙测量等模型技术受到限制,因此,实体模型对于回流区的模拟难以做到相似和准确,均会出现不同程度的偏离,例如,三峡库尾河段变态模型的港池回流区泥沙淤积量和淤积高程普遍比原型偏高。数学模型则不受模型相似、变率、比尺及测量等方面的限制。
回流区泥沙淤积计算严格地讲应该采用三维水流泥沙数学模型,但对于天然河道中常见的“封闭”竖轴环流,当水深相对较小、上下层水体掺混相对较弱时,采用水深平均二维水流泥沙数学模型进行模拟计算是可行的。由于回流区紊动掺混较为强烈,水流运动控制方程(N~S方程)中的对流惯性项与紊动粘性项均是主要控制项,因此,数学模型应该采用紊流模型(如κ~ε方程)进行紊动粘性系数νt和紊动粘性项的精细模拟。
2 二维水流泥沙数学模型
2.1 水流模型
水流控制方程采用水深平均(沿水深积分)平面二维非恒定流浅水方程(守恒型)[2,5,6]
| (1) |
| (2) |
| (3) |
式中X、Y、t分别为平面二维坐标和时间坐标;u、ν分别为水深平均流速分量;z、h分别为水位和水深;n、νt分别为糙率和率动粘性系数。
紊动粘性系数νt的精细模拟采用了水深平均平面二维κ-ε双方程模型(守恒型)[2,6]
| (4) |
| (5) |
| (6) |
其中 |
|
| (7) |
| (8) |
式中κ、ε分别为紊动动能和耗散率;Ph为κ的产生率;Pκν、Pεν分别为附加源项;U*为摩阻流速;σκ、σε、C1、C2 、Cμ、Cκ、Cε均为模型参数。
对于恒定流,去掉方程中的时间惯性项;水流模型定解边界条件采用进口给定流速u、v、紊动动能κ、耗散率ε和紊动粘性系数νt的分布,出口按法向边界条件控制;模型进口各变量具体按下列经验公式给出
| (9) |
| (10) |
方程(1)~(3)数值求解基于SIMPLER算法[1,5,6];方程(4)~(6)数值求解采用有限控制容积法[1,6]。
水流模型中主要参数的取值见表1
表1 水流模型主要参数取值 | ||||||
Main parameters of flow model | ||||||
σκ | σε | C1 | C2 | Cμ | E | Eκ |
1.0 | 1.3 | 1.44 | 1.92 | 0.09 | 1/2~1/8 | 0.05~0.10 |
2.2 泥沙模型
含沙量分布的模拟采用了平衡输沙模式下水深平均形式的泥沙对流扩散方程[5,7]
| (11) |
式中s为垂线平均含沙量;εs为泥沙紊动扩散系数(εs=κνt,h为经验系数)。
含沙量方程(11)边界条件仍采用进口给定分布,出口按法向边界条件控制;数值求解也采用了有限控制容积法[1,6]。
假定回流区外侧的纵向主流泥沙冲淤变化相对较小,采用平衡输沙模式可计算出整个回流区内的泥沙淤积量,计算公式为 | |
| (12) |
式中W为回流区泥沙淤积体积;Q为流量;Δt为计算时段;G1s为回流区上游进口断面的输沙率;G2s为回流区下游出口断面的输沙率;γ′为泥沙淤积物干容重。 |
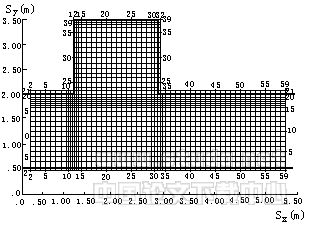
3 空腔回流区水沙特性分析 利用长江院空腔回流泥沙淤积水槽试验资料,进行了同一水槽边界四种模型变率的水流流场、含沙量分布及回流区泥沙淤积计算。四组水槽的计算水沙条件、主要参数取值见表2。计算采用非均匀正交矩形网格,网格间距为5~10cm,计算节点为60×40(图1)。 |
|
|
图2空腔回流区二维水沙计算流速矢量场 |
Vector field of calculated velocity |
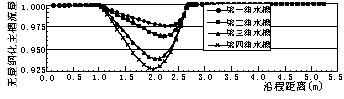
图2和图3给出了第一和第四组水槽回流区流速矢量场和相对流速等值线分布,相对流速是指回流区二维计算节点水深平均流速占水槽进口断面平均流速的百分数;图4给出了四组水槽计算的无量纲化主槽流量沿程变化,无量纲化主槽流量为空腔主槽区流量与进口流量的比值。
表2 空腔回流区二维水沙计算参数及成果 | ||||
Calculated parameters and results of 2-D model | ||||
计算组次 | 一 | 二 | 三 | 四 |
水深h(cm) | 10 | 25 | 50 | 70 |
流量Q(l/s) | 6.17 | 24.38 | 68.96 | 114.23 |
含沙量S(kg/m3) | 7.13 | 7.18 | 7.18 | 7.43 |
泥沙中值粒径d50(mm) | 0.09 | 0.17 | 0.30 | 0.35 |
放水历时t(min) | 360 | 227 | 161 | 136 |
进口流速U(cm/s) | 4.113 | 6.501 | 9.195 | 10.879 |
模型变率e | 1.0 | 2.5 | 5.0 | 7.0 |
Froude数Fr | 0.0415 | 0.0415 | 0.0415 | 0.0415 |
Reynolds数Re | 4110 | 16250 | 45975 | 76150 |
水槽糙率n | 0.012 | 0.012 | 0.012 | 0.012 |
实测回流区淤积① | 2.30 | 3.22 | 8.74 | 13.34 |
计算回流区淤积 | 3.66 | 6.27 | 8.88 | 10.64 |
注: ① 无量纲化泥沙淤积:100×(泥沙淤积体体积/回流区水体体积)。 | ||||
|
图3空腔回流区二维水沙计算无量纲化流速等值线 |
Calculated isopleth of velocity |
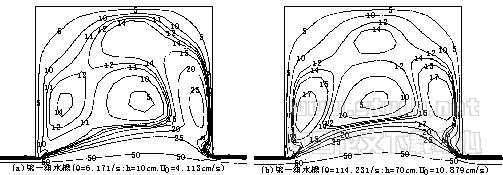
表2给出了四组水槽回流区泥沙淤积验证结果;图5给出了第一和第四组水槽回流区含沙量等值线;图6给出了二维数模计算的空腔回流区泥沙淤积量与主槽流量亏损的关系,泥沙相对淤积量和主槽流量相对亏损分别指不同模型变率条件下无量纲化泥沙淤积和无量纲化主槽流量亏损与模型变率1时(第一组水槽) 对应值之比,无量纲化主槽流量亏损为进入空腔回流区最大流量占进口流量的百分比;图7给出了计算的空腔回流区泥沙相对淤积量与模型变率的关系。 |
|
|
图5空腔回流区二维水沙计算含沙量等值线 |
Calculated isopleth of sediment concentration |
图6空腔回流区泥沙淤积量与主槽流量亏损的关系 | 图7空腔回流区泥沙淤积量与模型变率的关系 |
Relation between sediment deposition and discharge loss in main channel | Relation between deposition and distorted ratio of model |
上述计算成果不仅证明了回流区二维水流泥沙数学模型的可行性,验证了回流区泥沙淤积计算方法的精度,而且对于回流区环流、泥沙淤积以及模型变率对回流区水沙特性的影响等有如下几点认识:① 空腔回流属于竖轴环流,具有不对称性和不封闭性;回流区与主流区交界面(紊动掺混区)存在较大的流速梯度;水流从空腔下游侧壁进入回流区,以对流形式参与回流区环流运动;回流区环流运动受水流的紊动粘性项和对流惯性项的共同作用。② 回流区含沙量分布也呈现出不对称性;回流与主流交界面存在着较大的含沙量梯度,但其强度弱于流速梯度强度,表明回流区泥沙运动存在着滞后性;回流区泥沙淤积量与主槽流量亏损的关系表明:回流区环流特性决定了回流区泥沙特性及淤积量。③ 模型变率不同的空腔水槽,回流区环流形态及非常相似,但存在着环流中心及强度、进入空腔流量以及回流区水流紊动特性等方面的差异;模型变率不同的空腔水槽,回流区含沙量分布形态也非常相似,但回流区含沙量大小及泥沙淤积量差异较大;模型变率越大,回流区含沙量及水流挟沙力越小,泥沙淤积量越大;回流区泥沙淤积量与模型变率趋于线性关系,表明:变态模型均会出现回流区泥沙淤积量的不相似。
4 结语
1. 本文建立了回流区水深平均平面二维水流泥沙数学模型,提出了平衡输沙模式下回流区泥沙淤积计算方法;采用长江科学院空腔回流泥沙淤积水槽试验数据,验证了回流区泥沙淤积计算方法的可行性和精度;这一计算模式适用于水槽或天然河道最为常见的竖轴环流回流区环流及泥沙淤积计算。
2. 二维数模计算分析表明:空腔回流具有不对称性和不封闭性;回流区与主流区交界面存在着较大的流速和含沙量梯度,含沙量梯度强度弱于流速梯度强度;部分挟沙水流从空腔下游侧壁进入回流区,以对流形式参与回流区环流运动及泥沙淤积,回流区环流及泥沙运动受到水沙紊动粘性项和对流惯性项的共同作用;回流区环流特性决定了回流区泥沙特性及淤积量。
3. 二维数模计算分析还表明:模型变率不同的空腔水槽,回流区环流及含沙量分布形态非常相似,但存在着环流中心及强度、进入空腔流量、回流区水流紊动特性以及回流区含沙量大小及泥沙淤积量等方面的差异;回流区泥沙淤积量与模型变率趋于线性关系,表明:变态模型均会出现回流区泥沙淤积量的不相似;因此,对于重力相似的变态模型,变率的选择应考虑回流区泥沙淤积相似的偏离,并应对回流区泥沙淤积量进行修正。
1 [美]S.V.帕坦卡著,张政译。传热与流体流动的数值。北京:出版社, 1984.
2 [西德]W.罗迪著, 贺益英译。环境问题的紊流模型。北京: 水利电力出版社, 1987.
3 张瑞瑾。论环流结构与河道演变的关系。武汉水利电力学院学报。1963(2):1-15.
4 刘青泉。盲肠河段口门掺混区的泥沙扩散。泥沙研究。1995(2):11-21.
5 董耀华。弯道水流的基本特性及数值模拟。长江科学院院报。1996(1):25-29.
6 董耀华。河道温度及浓度场的平面二维数模研究。长江科学院院报。1997(2):22-26.