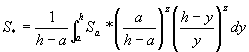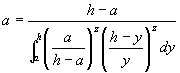剖面二维非恒定悬移质泥沙扩散方程的数值方法
摘要:通过讨论剖面二维非恒定泥沙扩散方程的数值方法,建立了一种用于求解含沙量分布沿程变化的差分格式(Z-C格式)并通过一个具体的数值例子说明了的方法步骤。
关键词:扩散方程 差分格式 精度 稳定性
1 引言
数学模拟方法正在成为研究河流泥沙问题的重要手段。目前,一维数学模型较成熟,已广泛应用于模拟长河段的长期变形,但它只能给出河段平均冲淤深度的沿程变化,如需了解短河段的河床变形细节,则要采用二维以至三维数学模型。不论是一维数学模型还是平面二维维数学模型,都不能反映含沙量沿垂线的分布状况,并忽略了含沙量沿垂线分布对垂线平均含沙量变化过程的影响。要解决这类问题,必须建立剖面二维数学模型。这种模型主要通过解剖面二维泥沙扩散方程来研究悬移质泥沙沿水深的分布及含沙量的变化过程,对水电站进口和其它引程的引水口高程的确定都能提供较好的数值模拟。
泥沙扩散方程实际上是一个变系数的二阶线性偏微分方程,这样的方程在各种复杂边界条件下求解是极为困难的。求扩散方程的解析解在数学上存在着难以克服的困难,往往只能通过对方程的简化,才能得到一些简单边界条件下的解析解,在这方面,A.A.Kalinske、野满隆治、W.E.Dobbins、俞维强、张启舜、韦直林[2]等都做了有益的尝试;求扩散方程的数值解曾经因为缺乏高效率的计算工具而难以实现,直到60年代后,随着计算机的广泛应用,在各种复杂边界条件下求扩散方程的数值解不但成为可能,而且得到迅速的发展,在这方面,曹志先、崔侠[4]等做了大量工作,取得了很多成果。
数值方法相对于解析方法在求解偏微分方程上有着明显的优势,即简单灵活、计算方便快捷,但要寻找一种精度高、稳定性好、计算方便的差分格式也并非易事。本文拟在前人研究的基础上着重讨论剖面二维泥沙扩散方程的数值解问题,希望能提供一种精度高、稳定性好、计算方便的数值解。
2 基本方程
剖面二维泥沙扩散方程的形式为 |
|
| (1) |
式中 x,y为水流方向和铅直方向的维轴;u,v分别为沿水流方向和铅直方向的时均流速;εsx,εsy分别为水流方向和铅直方向的泥沙扩散系数;ω,S分别为泥沙静水沉速和含沙量。
对于式(1)的求解,研究者一般会对它进行不同程度的简化,为此引入以下假定中的一种或几种:
| ||
|
C.在二维流动中,纵向扩散系数与方程其他项相比,可以忽略不计,即认为方程右端第一项可以忽略;
D.认为悬移质泥沙粒径均一,即ω=const;
E.认为水流为二维均匀流,即v=0。
为简单起见,我们讨论的范围限于水流条件为二维非恒定均匀流,悬移质泥沙粒径均匀,为此引入假定C、D、E。这时,泥沙扩散方程为
| (2) |
目前,对εs的变化研究得不很充分,一般假定 |
|
εs=βεm | (3) |
其中εm为动量传递系数,β为修正值。由勃兰特尔掺长理论可得
εm=κu*y/(1-y/h) | (4) |
式中κ为卡门常数,u*为摩阻流速。 |
|
对于u,我们取卡曼-勃兰特尔对数流速分布公式
(umax-u)/u*=(1/κ)ln(h/y) | (5) |
令W=ω+β(κu*/h)(1-2y/h),?则式(2)可变形为
| (6) |
3 差分方程 |
|
3.1 网格的剖分
?为建立差分方程,首先必须剖分网格。我们取时间步长?Δt=τ,X方向的空间步长?Δx=h1,Y方向的空间步长为Δy=h2,这样形成如下网格
Dh={(xj,yl,tn)|xj=jh1,yl=lh2,tn=nτ|} |
其中j=0,...,N; l=0,...,M;n≥0; |
3.2 构造差分格式
通过对流方程和扩散方程的差分格式的构造,我们可以得到对流扩散方程的差分格式。由于隐式格式稳定性好,考虑Crank-Nicholson型隐式格式。为此,引入差分算子记号
δ2ySnj,l=Snj,l+1-2Snj,l+Snj,l-1 |
LxSnj,l=Snj+1,l-Snj-1,l |
LySnj,l=Snj,l+1-Snj,l-1 |
为了看得更清楚,暂且取h1=h2=h.对式(6)离散,则C-N格式为
Sn+1j,l-Snj,l/τ+u/4hLx(Snj,l+Sn+1j,l)=εs/2h2δ2y(Sn+1j,l+Snj,l)+W/4hLy(Sn+1j,l+Snj,l) | (7) |
C-N格式的精度是二阶的,绝对稳定。但对于二维问题,由(7)导出的方程组,其系数矩阵不是三对角矩阵,不能用追赶法求解。因此,考虑构造交替方向的隐式格式(命名为Z-C格式)
(Sn+1/2j,l-Snj,l)/(τ/2)+u/2hLxSnj,l=εs/h2δ2ySn+1/2j,l+W/2hLySn+1/2j,l | (8) |
(Sn+1j,l-Sn+1/2j,l)/τ/2+u/2hLxSn+1j,l=εs/h2δ2ySn+1/2j,l+W/2hLySn+1/2j,l | (9) |
可以看出,Sn+1j,l是由两步组成的,每一步仅是一个方向的隐式,故用两次追赶法即可。
3.3 精度分析
现在,我们考虑Z-C格式的精度。先设法消去过渡值Sn+1/2j,l,为此,将(8)和(9)两式相加,可得
Sn+1j,l-Snj,l+τu/2hLx(Sn+1j,l+Snj,l)=τεs/2h2δ2ySn+1/2j,l+τW/4hLxSn+1/2j,l | (10) |
将(8)和(9)两式相减,可得 |
|
Sn+1/2j,l=(Sn+1j,l+Snj,l)/2+τεs/4h2δ2y(Snj,l-Sn+1j,l)+τW/8hLy(Snj,l-Sn+1j,l) | (11) |
把式(11)代入(10),变形整理,可得
(Sn+1j,l-Snj,l)(1-τuεs/8h3Lxδ2y-τ2uW/16h2LxLy)=(Snj,l+Sn+1j,l)(τuεs/2h2δ2y+τW/4hLy-τu/4hLx) | (12) |
设S(x,y,t)是(12)的精确解,并假定S(x,y,t)关于t三次连续可微,关于x,y四次连续可微,那么利用Taylor级数展开可得
S(xj,yl,tn+1)-S(xj,yl,tn)/τ(1-τ2εs/8h3Lxδ2y-τ2uW/16h2LxLy)-S(xj,yl,tn+1)-S(xj,yl,tn)/τ(τεs/2h2)δ2y+τW/4hLy-τu/4hLx)=O(τ2+h2) | (13) |
由此可见,Z-C格式具有二阶精度。
3.4 稳定性分析
现在,我们来讨论Z-C格式的稳定性。为此,把式(12)变形整理得
(1-τεs/2h2δ2y-τW/4hLy)(1+τu/4hLx)Sn+1j,l=(1+τεs/2h2δy2+τW/4hLy)(1-τu/4hLx)Snj,l | (14) |
由式(14)可得出过渡因子为
G(τ,k)=[(1-2τεs/h2sin2k2h/2+iτW/2hsink2h)(1-iτu/2hsink1h)]/(1+2τεs/h2sin2k2h/2-iτW/2hsink2h)(1+iτu/2hsink1h) | (15) |
令a=2τεs/h2sin2k2h/2,b=τW/2hsink2h,c=τu/2hsink1h,则
|G|2=|1-a2-b2+2bi/(1+a)2+b2|2·|1-c2-2ci/1+c2|2=1·(1-a2-b2)2+4b2/[(1+a)2+b2]2=1-4a2+4a+4b2+4a3/[(1+a)2+b2]2 | (16) |
显然,对于任意的τ,h,|G(τ,k)|2<1,?所以Z-C格式是绝对稳定的。
4 数值
4.1 边界条件
我们考虑初边值问题。
(1)初始条件
用Rouse公式给出含沙量沿垂线分布 |
|
S(x,y,0)=Sa·5(a/h-a)z(h-y/y)z | (17) |
式中z=ω/ku*为悬浮指标,Sa为近底含沙量,h为水深,一般取a=0.01~0.05h。 |
|
(2)水面条件 |
|
| (18) |
(3)底部边界条件 |
|
| (19) |
式中Sa*为近底挟沙力,即输沙平衡时的近底售沙量Sa.
(4)近底含沙量计算近底含沙量在求解泥沙扩散方程时具有边界条件性质,它选取的正确与否,意味着所给边界条件是否正确。实际工程中一般缺乏实测资料,近底含沙量不易测定。这里,我们利用水流挟沙力和含沙量沿垂线分布公式来反求近底含沙量[4]。
已知断面平均挟沙力为
S*=k(u3/ghω)m | (20) |
假定 |
|
Sa*=αS* | (21) |
输沙平衡时,含沙量沿垂线分布用Rouse公式(17)表示,用(17)表达挟沙力的垂线分布 ,然后沿垂线积分得断面平均挟沙力为
| (22) |
将(22)与(21)比较,可得 |
|
| (23) |
4.2 计算步骤
为方便计算,将式(8)和(9)式变形整理,并对X,Y方向取不同的空间步长
(τεs/2h22-τW/4h2)Sn+1/2j,l+1-(τεs/h22+1)Sn+1/2j,l+(τεs/2h22-τW/4h2)Sn+1/2j,l+1=τu/4h1LxSnj,l-Snj,l | (24) |
-τu/4h1Snj-1,l+Snj,l+τu/4h1Snj+1,l=τεs/2h22ζ2ySn+1/2j,l+τW/4h2LySn+1/2j,l+Sn+1/2j,l | (25) |
在一个时间层(第n层)内,计算分两步进行:
第一步,对式(24)用追赶法求第n+1/2层的过渡值。
令C1=-τu/4h1,C2=1,C3=τu/4h1,E1=τεs/2h22,E2=τW/4h2 |
D1=τεs/2h22-τW/4h2,D2=-τεs/h22-1,D3=τεs/2h22+τW/4h2 |
l=1时,D1Sn+1/2j,0+D2Sn+1/2j,1+D3Sn+1/2j,2=C3LxSnj,1-Snj,1 |
l=2时,D1Sn+1/2j,0+D2Sn+1/2j,1+D3Sn+1/2j,2=C3LxSnj,1-Snj,1 |
…………… |
l=M时,D1Sn+1/2j,M-1+D2Sn+1/2j,M+D3Sn+1/2j,M+1=C3LxSnj,M-Snj,M |
令Hl=-Snj,l+C3LxSnj,l (1<l<M) |
H1=-Snj,1+C3LxSnj,1-D1Sn+1/2j,0 |
HM=-Snj,M+C3LxSnj,M-D3Sn+1/2j,M+1 |
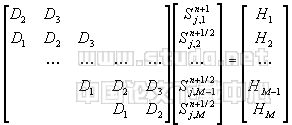
其中Sn+1/2j,0和Sn+1/2j,M+1由边界条件给出,则用矩阵形式表示为 |
| (26) |
第二步,再对(25)式用追赶法求第n+1层的值 |
令Fj=E1δ2ySn+1/2j,l+E2LySn+1/2j,l+Sn+1/2j,l? (1<j<N) |
F1=E1δ2ySn+1/21,l+E2LySn+1/21,l+Sn+1/21,l-C1Sn+10,l |
FN=E1δ2ySn+1/2N,l+E2LySn+1/2N,l+Sn+1/2N,l-C3Sn+1N+1,l |
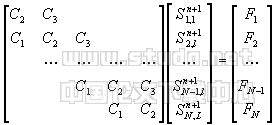
其中Sn+10,l和Sn+1N+1,l由边界条件给出,则同理可得矩阵方程 |
| (27) |
这样,按此步骤一层层地计算。
4.3 数值模拟合理性分析
受所掌握的实测资料的限制,目前尚无法对本文提出的算法与含沙量沿垂线分布的实测值进行对比。我们用库里·阿雷克沉沙池[5]的实测资料作了垂线平均值沿程变化的比较。该沉沙池的主要数据为:池深h=1.53m;平均流速u=0.12m/s;泥沙沉速ω=0.0176cm/s;悬浮指标Z=0.01。计算时取卡门常数κ=0.4,a=0.05h。表1给出了计算值和实测值,结果表明,计算值和实测值比较符合。
表1 断面平均含沙量验证(单位:kg/m3) | |||||||
Verifications of cross-sectional average sediment concentrations | |||||||
距离(m) | 0 | 200 | 400 | 600 | 800 | 1000 | 1200 |
计算值 | 3.012 | 2.573 | 2.071 | 1.639 | 1.209 | 0.849 | 0.539 |
实测值 | 3.012 | 2.650 | 1.810 | 1.520 | 1.141 | 0.822 | 0.561 |
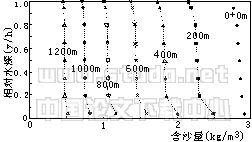
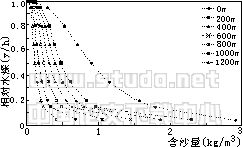
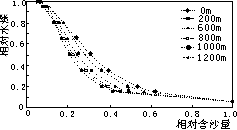
为了进一步分析含沙量垂线分布计算结果的合理性,我们对另一组较粗的泥沙(ω=0.616cm/s,Z=0.4)进行了对比计算。图1/,图2分别为两组沙的计算结果。从图中可以看出,计算结果符合含沙量沿垂线分布的一般,粗沙分布不均匀,细沙分布较均匀;近底浓度相对较大,水面浓度相对较小,不存在Rouse公式中水面含沙量为0的缺陷;含沙量沿程衰减的特性较为明显。图3为较粗一组泥沙的相对含沙量沿垂线分布的沿程变化情况。图3表明,尽管进口断面按Rouse公式给出了含沙量沿垂线的分布,但由于该断面实际处于不平衡输沙状态,这种分布并不是稳定的。在距进口200m处,泥沙的分布调整到一种不平衡输沙状态,随着泥沙的沿程淤积,水流输沙向平衡方向,垂线平均含沙量趋向于水流挟沙力,而含沙量沿垂线分布向平衡时的分布状态(Rouse公式)发展。由于这种发展是趋向于稳定状态,因此愈接近下游,分布愈靠近Rouse公式。计算结果表明,本文提出的计算方法是合理可行的。
|
|
图1 含沙量垂线分布的沿程变化(Z=0.01) | 图2 含沙量垂线分布的沿程变化(Z=0.4) |
Changes of vertical distributions of sediment ?concentrations(Z=0.01) | Changes of vertical distributions of sediment ?concentrations(Z=0.4) |
5 结语 本文建立了求解二维非恒定泥沙扩散方程的一种差分格式(Z-C格式)。这种格式具有如下特点: 1.精度较高(具有二阶精度)。 2.稳定性好(无条件稳定)。 3.计算较方便(每一时段利用两次追赶法即可)。 |
|
1 陆金甫,关治。偏微分方程数值解法。清华大学出版社,1987年7月。
2 韦直林。二度恒定均匀流中泥沙淤积过程的研究。武汉水利电力学院研究生,1981年11月。
3 张瑞谨,谢鉴衡等。河流泥沙动力学。武汉水利电力学院,水利电力出版社,1989年6月。4 崔侠。剖面二维数学模型的研究。武汉水利电力学院研究生论文,1988年10月。
5 韦直林。二度恒定均匀流中泥沙的淤积过程。武汉水利电力学院学报,1982年第4期。
6 韦直林,傅小平。论泥沙连续方程的建立及相关的几个问题。武汉水利电力大学学报,1997年10月第30卷增刊。