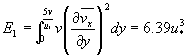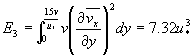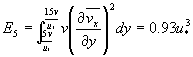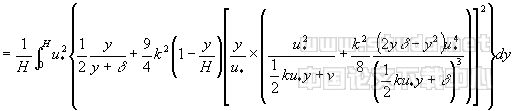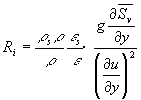低含沙水流运动特性综述
摘要:本文着重综述了清水水流(在固定—可动边界条件下)、挟沙水流的流速分布特征、紊动特性、能量间分配关系等流动现象的内部,并系统分析比较了它们的异同,文中还兼论了卡门常数。
关键词:清水水流 挟沙水流 流动规律
1 引言
拟序的研究丰富了人们对湍流的认识,近年来非线性的对湍流研究起了很大的推动作用。流体运动过程中的流速能量分布关系及其规律和猝发的特征及性质,一方面是研究挟沙水流等的基础,另一方面本身有其重要的理论意义和实践意义,本文探讨低含沙水流和清水特性的异同。
2 猝发现象
猝发现象的具体描述参见有关[1],研究表明:当Reh=uhυ(u为平均流速,h为水深)>10000时,用外部参量(u,h)无量纲化猝发周期T是不正确的,和混合参量(ν,h,u*,u)相比,最佳参量是用内部参量(ν,u*)无量纲化猝发周期并推导知:(u2*TB/υ≈190)(y+=yu*/υ≈+15)。[2]研究了零压力梯度下光滑平板和零压力梯度下表面糙度由粗糙向光滑转变时内部边界还未恢复局部平衡情形时的猝发规律。在猝发现象中,引射(Ejections)时对应的速度脉动为U′<0,V′>0,扫掠时,(Sweeps)对应的速度脉动为U′>0,V′<0,U′、V′分别为流向和法向脉动速度。正是引射所引起的动量、能量、涡度交换对内外层的相互作用有重要影响,进而影响摩阻流速的大小。[3]观察发现,每一个流层(位于缓冲层)中的流条上升都和对数层中的扰动有关,他们发现猝发和对数层作用所引起的扫掠对下游很远处的猝发产生都有影响,和扫掠相联系的对数层中的高剪切区是由展向涡或上翘流向涡(例如部分发夹涡)所引起的。[4]猜测局部的逆压梯度是由于上举所产生或引起上举的原因。[5]指出广泛存在于近壁区中的是j-形涡而非如原来认为的大量马蹄形涡。Morrison,J.F,Subamanian,C.S,P.Bradshaw采用象限分析法分析了扫掠(u′>0,v′<0,(U′、V′)以+为上标表示)和引射(u′<0,v′<0,(U′,V′)以-为上标表示)对U、V值的影响(为方便计在本猝发部分以小写的u、v示脉动值,以大写U、V示平均流速值),有
这里 |
| (1) |
r++r-=r | (2) | |
r约为0.5。易知对于一般其它量也应当满足下式 |
| |
| (3) | |
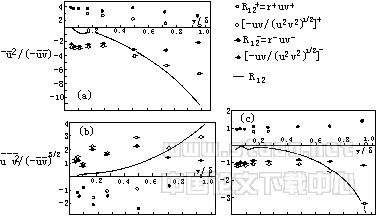
这里n≥0,m≥0,=表示湍流平均,-表示非湍流平均(为简单计,这里只讨论光滑情形)。 在外区,引射较扫掠更频繁发生,因而对当地剪切贡献更大,在内层中,二者对剪应力贡献大致相等,发生总时间也大致相同。在整个边界层厚度中,引射较扫掠对u′2和v′2贡献更大,二者之和约为40%的u2-uv和v2]-uv,由图1中易知引射和扫掠控制着能量和切应力的惯性传输。 |
|
经过推导知 |
| (4) |
由式可知:卡门常数是流体运动内部流场特性的参数,从一个局部平衡区到另一个局部平衡区,卡门常数也在变化,即卡门常数是一个反映流体运动特性的局部量,是空间点坐标和时间的函数,但卡门常数又是流体运动性态的一个系统整体参数,而非独立的变量。准确地讲,又称之为卡门参数。[6]分析了 |
?在边壁可动情形下的猝发情况研究近来也取得了一些成果,[7]研究了在不同密度的淤泥质床面上水流运动的猝发周期并和刚性床面的结果作了比较。结果表明,按内部参量T+B=u2*/v![]() 无量纲化的猝发周期,较同条件的清水在近壁区明显增大。
无量纲化的猝发周期,较同条件的清水在近壁区明显增大。
文献[8]的研究结果表明,悬浮泥沙的尺寸和波数增加,将使底壁水流更容易猝发,流动雷诺数增加将抑制猝发;泥沙的纵向流速比水流纵向流速大得愈多,愈不容易导致流体猝发的形成,但当泥沙的纵向流速比水流的纵向流速为小时(天然情形中常常这样),较易导致猝发的产生。[9]的研究表明,泥沙尺寸在一定范围内愈大,将使猝发次数增加,使湍流度和雷诺应力增加;泥沙含量增加,使猝发频率和流条平均空间尺寸不变。观察表明,似乎是近壁区的低速流条的上升和破裂控制着泥沙的传输,泥沙大部分在低速流条区积聚,后被流体上举带离床面,开始运动的。[10]的研究再一次表明,猝发历时随壁粗糙度的增加而减少。顺便指出,[11]研究高分子减阻中,相同摩阻流速条件下,减阻液和清水中两种情形下猝发历时和猝发空间长度之比值都近似为一常数值,约为1.67。
3 平均流速和脉动流速
3.1 流速分布
对流速分布的研究(这里以明渠为研究对象)人们作了大量工作,自从普朗特提出流速分布的对数公式后,50年代[12]曾给出了在整个边界层都适用的流速分布公式
umax-u/u*=1/kln(δ/y)+π/k f (y/δ) | (5) |
式中 k为卡门常数,δ为边界层原子度,π/k f (y/δ)为尾流函数。据[13]~[14]的研究,在明渠中,可以认为对数率一直适用到水面,即认为尾流函数为零。这里采用窦国仁流速分布公式
| (6) |
式中u为距壁面y处的时均流速,rl和rt分别为层化和率流的发生率。 vl、vt分别为层流和率流的流速成分布,其它符号参看[13]。
从湍流的内部入手,研究流速分布是一个重要的方向。[15]通过研究后得出,令Φ=u/u*,η=u*y/υ,则光滑边壁时外区流速分布可表示为
| (7) |
在上述流速分布公式中,对如下变换群变换,其形式保持不变 | |
υ1=λυ,u1=λ-αu | (8) |
上述变换也称之为重整化群变换,(α为重整化群参数)。 | |
在粗糙和过渡情形时,[16]经过研究后认为令 | |
| (9) |
则可得包括光滑、过渡、粗糙在内的明渠流速的分布公式为 |
|
| (10) |
易知,在上述流速分布公式中,若令 |
|
| (11) |
则上式在上述变换群变换下其形式保持不变。应当指出公式推导的物理基础是外流区,对近壁区其物理假定并不成立,但却开辟了一条从流体内部入手分析其流速分布的途径。
3.2 脉动
明渠紊流的脉动采用窦国仁提出的下述公式
| (12) |
| (13) |
| (14) |
式中 k为卡门常数,δ为边界层原子度, 董曾南在光滑壁面明渠均匀紊流的试验中将水流沿水深方向依次划分为粘性底层、过渡层、紊流层,其紊流度(标征 |
|
若平均流速和脉动流速均采用窦国仁公式,取 | ||
| (15) | |
| (16) | |
| (17) | |
| (18) | |
| (19) | |
平均流粘性耗散能相对于E?3所占的百分比 | ||
? 若u*y/υ∈[0,5] 则E1/E3=87.3% | (20) | |
若u*y/υ∈[5,10] 则E2-E1/E3=9.2% | (21) | |
若u*y/υ∈[0,10] 则E2/E3=96.5% | (22) | |
若u*y/υ∈[10,15] 则E4/E3=3.4% | (23) | |
顺便指出 | ||
=u2*/2H×[H+δln(δ/(H+δ))]+9/2H2k2{[υ2(a1-4b1)+4(b21-a1b1-2c1)υ+(a1b21-2a1c1+4b1c1)]×(1/υ-2/a1)+1/2×[1/υ2-(2/a1)2]×[2(a1b1-b21+2c1)υ2+2(a1c1-a1b21-4b1c1)υ-2c1(a1b1+c1)]+1/3×[1/υ3-(2/a1)3]]×[a1b21-2 a1c1+4b1c1)υ2+4c1(a1b1+c1)υ+c21a1]+1/4[1/υ4-(2/a1)4]×[-2c1(a1b1+c1)υ2-2a1c21υ]+ a1υ2c21×1/5[1/υ5-(2/a1)5]+lna1/2υ×[-2υ2+2(4b1-a1)υ+2(a1b1-b21+2c1)]+[a1/2-υ]×[(a1+4v)-4b1]-[(a1/2)2-υ2]} | (24) | |
上式中 a1=Hku*+2υ,b1=ku*δ+2υ,c1=ku*δυ+υ2.顺便指出, | ||
| ||
3.3 湍流现象
其实针对湍流概念,[18]给出了一个极好的描述,它联系了涡运动与紊运动的物理关系,以及表达了紊运动在时间和空间上都是一种局部现象。
令1/λt=粘性应力/紊动应力=[μ(du/dy)]/-ρu′v′ | (25) |
对于充分紊流取u*δ/υ≈11,u*y/υ≈12,k=0.4知(采用窦国仁公式) | |
λt≈1.5 | (26) |
在湍流流速场分布中,[19]找到了如下的速度场之间的广义自相似性关系 | |
x′=λx,t′=λt1-β,V′=λβV,(p/ρ′)=λ2β(p/ρ),υ′=λ1+βυ | (27) |
其中β为标度指数。 | |
针对柯尔莫哥洛夫的湍流物理图象,[20]提出了β模型。由β模型知,令间歇现象的维数为D,则 | |
| (28) |
vn∝∈1/3ln1/3(ln/l0)(D-3)/3 | (29) |
Tn∝∈-1/3ln2/3(ln/l0)(3-D)/3n | (30) |
En∝∈2/3ln2/3(ln/l0)(3-D)/3 | (31) |
易知D=3时,ld=(∈υ-3)-(1/4)即为柯尔莫哥洛夫的耗散尺度。 | |
出现上述结果的本质,在于流体运动都受控于Navier Stokes方程。因而出现流体运动时均流速和流动特征等流体运动所固有的特性。
分析猝发现象中关于k值的论述和[21]~[26]、窦国仁、练继建、洪柔嘉等的研究结果,k值大小直观的讲,和流速分布梯度有关,[24]对此作了最为详细的研究。k值似乎和雷诺应力关系密切,这在[25]的试验结果中看的更为清楚。换言之,卡门常数和流体运动过程中能量分配关系有关。
4 低含沙水流运动
?对于理查逊(Richardson)数的解释,一般认为代表单位水体在单位时间内就地消耗的能量中,用以克服密度梯度消耗的能量所占的比例,可以写为
| (32) |
[26]的研究表明,理查逊数亦可写为悬浮功与时均流提供的脉动能量之比,即 | |
| (33) |
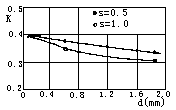
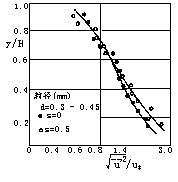
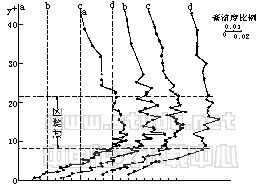
含沙水流(轻质低含沙浓度可用激光测速仪实测)试验成果表明与相同条件的清水水流相比,水流的时均和脉动的确发生了相应的变化。时均流速分布仍为对数分布律,其中卡门常数k值随含沙浓度的增加而减小,而脉动强度则随含沙浓度的增大而加剧。卡门常数和脉动强度不仅与含沙浓度有关,而且还与颗粒粒径大小有关。在相同含沙浓度情况下,卡门常数随粒径的增大而减小,脉动强度则随粒径的增大而增加。和清水相比,在外区二者脉动强度相差不大,如图3、4所示。
?含沙水流中能量分配图象和清水水流的比较参看高含沙水流中结合实测成果的论述(结果容易推广到低含沙水流)。
5 讨论
上述湍流流动所具有的特性,从物理性质上而言是流体自身所具有的特性,是由流体流动自身所遵循的物理所决定的;从数学上而言,是控制流体运动的N S方程在特定边界条件下的性态的体现。壁的影响导致湍流流动的内外区拟序本质性的不同,而湍流流动中内外区的相互作用和影响正是通过猝发完成的。湍流内部的特殊剪力场、流速分布特性、能量分布特性、内部精细等和猝发有着密切的不可分割的联系。图1清楚展示了猝发所具有的特征,清楚展示了描述猝发的物理量的分布和在猝发过程中各量的变化情形。猝发的这种特性,是流体运动中确定性和随机性辩证统一的体现。
|
|
卡门常数的表达式表明,在流体流动的局部区域卡门常数是和流体运动的自身性态相关联的,和流体内部的微密切有关,是由流体运动性态所决定的一个参数,这和[25]中实验结果表明的卡门常数和雷诺应力有关相吻合。
湍流的β模型是对湍流概念的一种定量化说明,在[18]所给的湍流概念中,清楚揭示了湍流现象无论在时间和空间上都是一种局部现象。近代实验结果表明其中的能量现象也具有局部的特性,采用窦国仁的平均流速和脉动流速公式,笔者详细给出了其中的能量分布关系,尤其是脉动能量的分布关系,这和[14]实测的表征湍流度的实验结果相吻合。
在湍流流速分布表达式中,对一些重整化变换其形式保持不变,即速度场之间有广义的自相似性关系,这从一个侧面说明了对于流体运动,只要连续介质假定成立,控制其运动的方程均为N S方程。重整化群、分形、混沌、小波变换理论均是从不同侧面对湍流性态的刻画,因而所得结果在物理特性的解释上有本质性共同的特征。虽然法国的南安普顿学派从数学上探讨湍流取得了很大进展,众多学者一直在作持续努力,但距问题的真正解决相去甚远。近年来,人们对猝发进行了大量精细的研究,但到目前为止,仿佛还没有一个可被普遍接受的描述猝发过程的定量化模式,以阐述猝发在湍流运动过程中的作用和意义。因而对于流速(平均流速和脉动流速)分布的解析表达式,似乎对流体内部的反映的不充分,对于非平衡、非恒定条件下的流体运动普遍性质的阐述,好象涉及到湍流发生本质的非线性问题。
6 结论
挟沙水流运动和清水水流相比,有其自身的作用、特性,而理解清水水流的运动规律则是研究挟沙水流和高含沙水流运动的基础。本文综述分析了清水水流和挟沙水流的流速分布特征、紊动特性、能量间分配关系等流动现象的内部规律,并比较了它们的异同,为理解高含沙水流运动特性作了准备。
1 夏震寰。水力学(三),紊流力学。北京:高等出版社,1992。
2 Morrison,J.F.,C.S.Subramanian and P.Bradshaw,Bursts and the law of the wall in turbulent boundary layers.J.Fluid Mech.1992,241.
3 Offen,G.R.and Kline,S.J.Combined dye streak and hydrogen bubble visual observations of a turbulent boundary layer.J Fluid Mech.1974,62.
4 Offen,G.R.and Kline,S.J.A proposed model of the bursting process in turbulent boundary layer.J.Fluid Mech.1975,70.
5 Robinson,S.K.Coherent motions in the turbulent boundary layers.Ann.Rev.of Fluid Mech.1991,23.
6 Krogstad,P.A.Antonia R.A.and Browne,L.W.B.Comparison between rough and smooth wall turbulent boundary layers.J.Fluid Mech,1992,245.
7 练继建,洪柔嘉。淤泥质床面上减阻流动的紊动特征。水利学报,1995,9.
8 林建忠,沈天耀。挟沙水流中沙粒对底壁湍流猝发的影响。水利学报,1994,5.
9 Rashidi,M.Hetsroni,G.and Banerjee,S.Particle turbulence interaction in a boundary layer.Int J Multiphase flow,1990,16.
10"Mutlu Sumer,B.and Rolf.Deigaard.Particle motions near the botton in turbulent flow in an open channel.Part 2 J.Fluid Mech,1981,109.
11"Luchik,T.S.and Tiederman W.G.Turbulence structure in low concentration dragreducing channel flows.J.Fluid Mech.1988,190.
12"Coles.D.The law of the wake in the turbulent boundary layer.J.Fluid Mech 1956,1.
13"窦国仁。明渠和管道中层流和紊流的总。A,1982,5.
14"董曾南,丁元。光滑壁面明渠均匀紊流水力特性。中国科学A,1989,11.
15"Barenblatt.GI.Scalling laws for fully developed turbulent shear flows.J.Fluid mech.1993,248
16"肖勇等。固壁紊流流速分布指数型公式和阻力规律。水科学进展,1997,2.
17"刘兆存。二维平行壁面剪切流失稳内部初探。水动力学研究与进展(已接收).
18"杨文熊。湍流一般机理及其应用。力学进展,1992,4.
19"刘式达等。流体运动中的广义自相似性和标度不变性。科学通报,1997,2.
20"Frisch,U etal.A simple dynamical model of intermittent fully developed turbulence.J Fluid Mech.1978,87.
21"钱宁,万兆惠。泥沙运动力学。北京:科学出版社,1983.
22"Giselher,Gust.Observations on turbulent drag reduciton in a dilute suspension of clay in sea water I Fluid Mech.1976,1.
23"Luchik,T.S.and Tiederman,W.G.Timescale and structure of ejections and bursts in turbulent channel flows.J.Fluid Mech.1987,174.
24"秦荣昱等。河流推移质运动理论及应用。北京:中国铁道出版社,1996.
25"陈长植等。曲率缓变型反弧段水流的紊动特性。水利学报,1994,10.
26"李福田。挟沙水流紊动的实验研究。泥沙研究,1986(1).

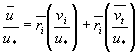
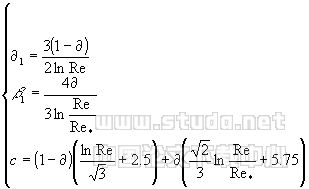
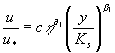
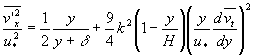
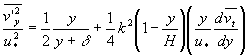
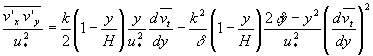
 ,则有
,则有