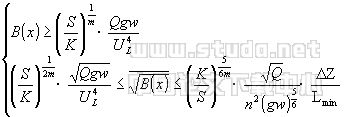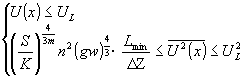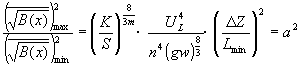分析河相关系时的补充条件分析
摘要:本文从水流泥沙运动方程出发, 通过附加河流边界条件的方法, 分析了河相关系并给出了顺直型、弯曲型及分汊型河流形成的必要条件。但由于很多影响河相关系和河型形成的其它因素没有考虑, 因此本文只是对实际情况的简化分析。
关键词:边界条件 河型 河相关系
1 河相关系研究现状
早期河相关系的研究基本上是属于经验性质的。具体的作法是:选取比较稳定或冲淤幅度不大、年内接近平衡的可以自由的人工渠道和天然河道进行观测,在形态因素与水力泥沙因素之间建立经验关系,如早期的流速比降等经验关系式。随着河相关系的研究得到不断的发展和完善,现已取得了很多的研究成果,其中不少的河相关系式已不再是纯经验性的,具有一定的理论基础。
从水流泥沙运动方程出发研究河相关系也已有不少成果,具有理论化的特点,这些方程是
水流连续方程 | Q=BhU | (1) |
水流阻力公式 | U=1/nh2/3J1/2 | |
水流挟沙能力公式 | S=S*=Ks(U3/ghw)m |
要求解未知量B、h、U、J尚需增加一个方程,目前增加一个方程的办法有很多种,如临界起动假说、最小活动性假说、最小功原理、最小方差理论和引入某种“原生河相关系式”的经验方法等。河流边界条件在河相关系中起着重要的作用, 这早已引起了人们的重视, 不少学者已对此作过分析和实验研究。通过引入一定的河流边界条件也可以求解方程组(1)。且事实上人们早已用水流泥沙运动方程通过引入一定的河流边界条件的办法求解了河床形态问题,这就是一维、二维和三维水流泥沙数学模型, 数学模型的最基本方程即是方程组(1)。人们在利用数学模型求解河床变形时,一般又都未明确提出其引用的边界条件和说明为什么引用其采用的边界条件,这就不可避免地有时在冲淤时引入了不恰当的边界条件,使得计算结果的可靠性受到了影响。此外用数学模型求解河床变化时不但要求解B、h、U、J未知数, 还应模拟河型变化, 否则不能完满地解决生产问题。例如用一维模型模拟冲积性河道的河床变化, 这时方程组(1)是可解的。但此时河型的变化是未知的, 即河道长度的变化是未知的, 因此河床高程的变化严格地说仍然是未知的。因此分析方程组(1)在不同的边界条件下的河相关系应与河型分析相结合, 这对数学模型的研究具有重要意义。
2 河流及其边界条件
从水流泥沙运动方程出发研究河相关系,须提供一定的河流边界条件。具体提供怎样的边界条件,应视河流的具体情况而定。河流边界条件包括进出口断面边界条件、河岸边界条件和河床边界条件。
2.1 进出口断面边界条件
这里指进出口断面的水流边界条件。河相关系是在一定水流条件下的河相关系,研究河相关系要结合水流边界条件来研究。河道一般为缓流,进出口水流边界条件这里按两类形式给出。第一类是进口断面流量已知,出口断面水位已知,即
| (2) |
第二类边界条件是流量已知, 进出口断面水位流量关系已知。进出口水位流量关系已知, 相当于进出口水位差已知, 即 | |
| (3) |
这种边界条件提法在定床水流计算是错误的, 但研究河相关系时是可以的,因为这时断面形状是未定的。而河流的起点和终点水位必须是给定的, 这是由泥沙从上游往下游的单向输移性所决定的, 泥沙输移不能在起点造成淤积, 起点的夷平过程应作为已知的。
2.2 河岸边界条件 河岸边界条件指河岸的抗冲性边界条件,由于河岸的淤积物本身有可能是由水流挟带的泥沙淤积而成, 因此河岸的抗冲强度有时是来水来沙的函数。河岸的抗冲强度可用河岸的抗冲剪应力等表示,为了讨论方便, 这里用河岸的抗冲流速表示。若用UL代表河岸能抗拒的最大水流流速,则河岸稳定的边界条件为 |
| |||
U≤UL | (4) |
这里U应为岸边流速, 岸边流速与断面平均流速是不同的, 但为了分析简单,这里认为两者相等。
2.3 河床边界条件
河床边界条件指河床的抗冲性边界条件,当不考虑推移质运动时,可用悬移质挟沙能力的非饱和系数Ps来表示,方程组(1)悬移质输沙平衡方程改为
S=Ps·Ks·(U3/ghw)m=K·(U3/ghw)m | (5) |
输沙平衡,河床稳定的条件为 |
|
Ps≤1 | (6) |
Ps可以看作是悬移质在床沙中所占的百分比。Ps=1时床沙与悬沙粒配相同,为非抗冲输沙平衡。Ps<1时床沙粗化,河床抗冲性大。
3 几种简单边界条件下的河相关系
河流的边界条件一般很复杂, 只能结合水流泥沙运动方程求数值解, 这里就几种简单的边界条件从水流泥沙运动方程分析河相关系与河型。
3.1 河岸起控制作用的河相关系
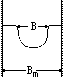
进出口断面边界条件为流量已知, 出口水位已知。河流位于两抗冲岸壁之间,岸壁间的距离为Bm。如图1所示, 假定河宽B小于Bm, 此时河岸由悬沙淤积物组成, 抗冲流速为UL。这时水流泥沙运动方程加上边界条件为
| (7) |
由上面的方程组可知,河岸稳定条件等价于 |
|
B≥S(/K)1/m·gwQ/U4L | (8) |
若UL较小,满足 |
|
(S/K)1/m·gwQ/U4L≥Bm | (9) |
则淤积物河岸不能稳定,会被水流冲走,直到抗冲岸壁起到控制作用为止,因此必有B=Bm,条件(9)代入(7)式还给出
J≥(BmQ)4/3·UL10/3n2=Jmin |
|
即 ΔZ≥(BmQ)4/3·UL10/3n2·L | (10) |
由方程组(7)可得完全由河岸起控制作用下的河相关系为 | |
| (11) |
某些水槽实验、渠化河道、狭谷河段、冲积性河流中的险工护岸段或洪水期等,可能完全由河岸起控制作用,河相关系属于这种情况。判断是否完全由河岸起控制作用的条件为同时满足(9)式和(10)式, 即进出口高差较大, 河岸约束较紧。由(11)式可知, 完全由河岸起控制作用时的河相关系与进出口水位差无关。? 当河岸起到完全控制作用时,若进出口水位差ΔZ也是已知的,则可能出现下面两种常见现象:
当时Jmin·L<ΔZ<J·L时,则出现下游水位对入流的顶托现象
当ΔZ>J·L时, 则河道纵剖面会不连续, 形成跌水, 如山区河道的瀑布。
3.2 完全由进出口边界条件起控制作用下的河相关系
完全由进出口边界条件起控制作用下的河相关系,这里指进出口给定第二类边界条件(3)式。进出口边界条件对河相关系起控制作用。而河岸的抗冲流速较小,河岸对水流没有起控制作用。先假定河岸边界条件起控制作用, 则水流泥沙运动方程加边界条件为
| (12) |
由上面的方程组可得河岸的稳定性条件等价于 | |
J=(S/K)4/3m[n2(gw)4/3/U2]≥(S/K)4/3m[n2(gw)4/3/U2L] | (13) |
用Lmin代表进出口断面间的最短距离,则有 | |
| (14) |
当ΔZ较小,满足 | |
|
| |||||||||
| (17) |
可见B小的地方U大、J小,B大的地方U小、J大,河道的平面形态如图2所示。由于河岸边界是活动的,B大U小处河岸移动慢,河岸相对来说较为稳定;而B小U大处河岸移动也快, 河宽、比降会变大。又因为进出口高差一定, 因此河窄处比降变大必造成河宽处比降变小。由(17)式可知, 宽处比降变小后河宽会变窄, 流速会变大。最后流速、河宽、比降沿程趋于不变。又因为J最大时U最小,河岸相对来说最为稳定,因此必有
| (18) |
这说明河道必是顺直型的。但由于扰动的存在,实际上河宽会有所波动,水深、流速和比降的分布也是如此。天然河道中岸边线犬牙交错,向下游不断移动的情况是常见的。游荡性河流岸边界剧烈摆动的情况也是常见的。
综上所述,完全由进出口边界条件起控制作用下的河相关系为
| (19) |
断面宽深比为 | |
| (20) |
判断河相关系是否完全由进出口边界条件控制的标准为U≥UL,即式(15)。由(19)式可知, 完全由进出口边界条件起控制作用时的河相关系与河岸的抗冲强度无关。此外UL/U的值也可以作为顺直型河道形成的必要条件。令
α=(UL/U)2=(K/S)4/3m·[U2L/n2(gw)4/3] ·ΔZ/Lmin | (21) |
当α<1时岸边界是不稳定的,河道是顺直的,α愈小,岸边界愈不稳定。因此α较小是顺直性河道形成的必要条件。
3.3 进出口边界条件和河岸边界条件均起控制作用下的河相关系
3.3.1 前提条件
进出口边界条件和河岸边界条件均起控制作用下的河相关系在这里指:进出口边界条件为第二类边界条件(3)式。河岸稳定性条件得到满足,则水流泥沙运动方程加上边界条件为
| (22) |
3.3.2 河相关系 | |
由方程(22)可得(13),设J的最短距离, 则有 | |
| (23) |
由(23)式有Lmin≤L≤(K/S)4/3m·[(ΔZ·U2L)/n2(gw)4/3] | (24) |
由上式可知,进出口断面边界条件和河岸边界条件同时对河相关系起控制作用时,即上式成立时,应满足 | |
ΔZ≥(S/K)4/3m·[n2(gw)4/3/U2L]·Lmin | (25) |
又:h=(K/S)1/mU3/gw,J=(S/K)2/3m·n2·(gw/h)2/3, 有 |
|
| (26) |
又 |
|
| (27) |
又J=(S/K)4/3m·n2·(gw)4/3/U2有 |
|
| (28) |
综上所述,进出口断面边界条件和河岸边界条件同时对河道形态均起控制作用时的河相关系为(23)至(28)式。河相关系是否既受进出口边界条件控制又受河岸边界条件控制的判别标准为(25)式。
3.3.3 进一步讨论
(23)式至(28)式给出的河相关系各值都有一定的变化范围。其中河段长度L的变化范围可以作为形成弯曲性河道的必要条件。
Lmax/Lmin=(K/S)4/3m·[U2L/n2(gw)4/3]·ΔZ/Lmin=α | (29) |
α较大是弯曲性河道形成的必要条件。弯道形成后,由于弯道环流的存在,条件允许时,河道会尽量地弯曲,并向下游,直到河长达到(24)式中给出的最大河长。
(27)式中河宽平方根平均值的变化范围可用来反映分汊性河道的总体特征,即
| (30) |
可见α较大时才有可能形成分汊河段。但α较大时河道是弯曲型河道还是分汊型河道应视其它具体情况而定。
4 分析
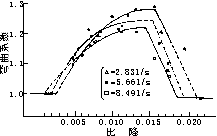
通过上面的分析得到了几种简单边界条件下的河相关系和河型形成的必要条件判别值α。这里没有专门针对这些结论进行实验验证。但目前已有很多人针对河型成因问题进行过实验和野外观测研究。如Edgyar用松散的含有粘性成份的天然沙在不同比降、不同流量(定常流量)下的实验,给出了弯曲系数与比降的关系,如图3。Edgyar还给出了天然河道调查资料,弯曲系数与比降的关系是相似的。其实验和调查结果得出的结论为:河道的河型转变存在一个临界比降(不同河道具有不同的临界比降值)。当河槽比降小于临界比降时河道是顺直的, 当比降大于临界比降后出现弯曲性河道。当比降进一步增加后, 河道变为辫状分汊河道。这些与本文的分析结论是一致的。同时野外观测和实验都说明河道的弯曲系数不是与比降完全成正比的,这可能与本文的分析中没有区别河道的平均流速与岸边流速有关, 河道的断面形状不同, 弯曲形状不同, 断面上的流速分布是不一样的。另外一些人的实验研究如Ackers的研究说明,当河岸组成物质缺少粘性成份时, 不能形成真正的弯曲河道。这与本文的分析结果也是一致的,因为缺少粘性成份时,一般来说河岸的抗冲流速小, 而α与U2L成正比, 可见河岸的抗冲流速小, 是难以形成弯曲河道的。针对河型成因的研究, 国内也有很多人作了试验研究, 试验结果是相似的。
本文的分析结论,在水库淤积引起的河型变化方面能说明问题。河道上修建水库后,一般上游来水来沙条件变化不大,主要表现为比降变化。如丹江口水库变动回水区, 由于修建水库后水面比降调平, 河道淤积,河道向顺直窄深方向发展。又如三门峡水库修建后由于潼关水位的抬高, 渭河下游弯曲系数变小;而当三门峡水库改变运行方式, 潼关水位下降后,渭河下游的弯曲系数又基本恢复。但建库后下游河道的变化就比较复杂,因为建库后下泄水沙条件一般都会发生变化, 河道冲刷、比降及河床和河岸的抗冲性都会发生变化,α值的变化方向各河道会不一样,因此河型的变化也就不一样。 |
|
5 结语
1.本文通过引入不同的河流边界条件,分析了从水流泥沙运动方程得到的河相关系,同时给出了形成顺直型河流、弯曲型河流和分汊型河流的必要性判别条件。由于本文对河型的分析是从河流的平面形态出发的,不涉及河流的运动特性,因而不涉及以运动特性作为分类标准的游荡型河流的概念。河型成因是一个复杂的问题,本文对河型成因的分析还有很多因素未能考虑。
2.本文的讨论用的是一维水流运动方程,因此断面形状只能概化为矩形,同时未考虑流速在河宽上的分布,没有考虑岸边流速与断面平均流速的不同,与实际情况有一定的差别。利用二维或三维水流运动方程,给定复杂的边界条件来研究河相关系与河型问题则只能采用数值的方法。
?3.用泥沙数学模型模拟河流形态时, 由于考虑了河流的平衡演变过程, 因此河流的边界条件只需给定初始边界条件, 即河流的初始形态和组成。给定了河流的初始形态, 初始时刻进出口断面的水位差也就已知了, 这与理论分析是不一样的。因为理论分析是直接分析河流平衡时的形态, 不考虑平衡过程, 这样所有的边界条件只能是终了时刻的边界条件。
一维泥沙数学模型模拟河流的发展过程时,都假定河流的长度固定不变, 因此严格地说它只适用于3.1节中所述的河岸起完全控制作用时的情况;目前二维泥沙数学模型大都未考虑岸壁的稳定性问题,或不能很好地反映河岸的稳定性。因此现有二维泥沙数学模型严格来说只适用于三种情况:一是单纯淤积或微冲情况,因为此时没有岸壁稳定性问题;二是河相关系完全由河岸起控制作用时的情况;三是河相关系完全由进出口边界条件起控制作用, 而河岸没有起到控制作用的情况。要准确地模拟河道形态变化, 则只有采用三维水流泥沙运动方程,并考虑河岸与水流的相互作用和河岸的稳定性条件才有可能, 有待深入研究。当然现有的数学模型仍然是有用的, 只是适用范围受到了限制。
1 钱宁,张仁,周志德。河床演变学。出版社, 1987年。
2 K. J. Gregor. River Channel Changes. A Wiley-Interscience Publication, 1977.
3 明宗富。冲积河流的河相关系。泥沙研究, 1983(4).
4 姚爱峰,刘建军。冲积平原河流河型稳定性指标分析。泥沙研究, 1995(3).
5 许炯心。水库下游河道复杂响应的试验研究。泥沙研究, 1986(4).
6 林承坤。河型的成因与分类。泥沙研究, 1985(2).
7 Schumm S. A. et al. Experimental Study of Fluvial System. John Wily and sons, NY 1987
8 Dorland E. Edgar. The Role of Geomorphic Thresholds in Determining AlluvialChannel Morphology. River Meandering, Proceedings of the Conference River'83
9 Ackers, P. Experiments on Small Streams in Alluvial. Journal of the Hydraulic Division, ASCE, Vol.90, No. HY4, July, 1964
10"尹学良。弯曲性河流形成原因及造床试验初步研究。地报,第31卷1965(4).
11"杜殿勖,戴明英。三门峡水库修建前后渭河下游河道泥沙问题的研究。泥沙研究, 1981(3).
12*"杨积武。黄河下游河型分异及游荡性河型形成原因的探讨。第二届全国泥沙基本理论研究学术讨论会集, 建材出版社, 1995年。
13 Jean A. Cunge. Feasibility of Mathematical Modeling of Meanders. RiverMeandering, Proceedings of the Conference River'83
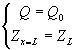
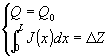
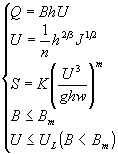
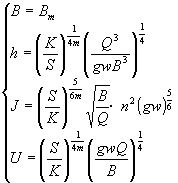
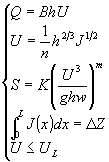
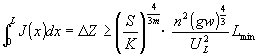
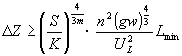
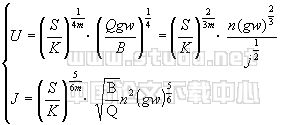
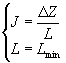
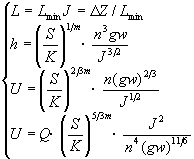
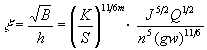
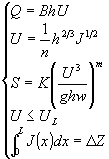

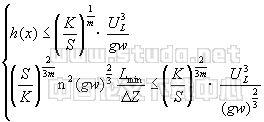
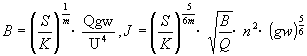 ,有
,有