基于EGARCH模型的交易所国债市场波动性分析
一、问题的提出
国债市场是运行中一个不可或缺的重要组成部分,联结货币政策和财政政策,沟通货币市场和资本市场。目前,我国国债市场结构分割,银行间债券市场与交易所债券市场构成国债市场的主体框架,银行间市场参与机构较少,形成寡头垄断;交易所市场参与者众多,形成竞争机制。在交易所市场中,通过买卖双方的竞争机制决定价格,其交易过程透明,形成的交易价格公正、公平。[1]
波动性(Volatility)是资产收益的不确定性的衡量,测度资产的风险。一般而言,波动性越大,风险越大。Engle(1982)首先提出的自回归条件异方差模型?即ARCH模型 将方差和条件方差区分开来,并让条件方差作为过去误差的函数而变化,从而为解决异方差问题提供了新的途径。Bollerslev(1986)提出了广义自回归条件异方差GARCH 模型。国外学者将这种方法应用到经济的诸多领域,显示了ARCH模型族的适用性。国内也有学者应用ARCH模型族对证券市场进行了实证研究,黄后川、陈浪南(2003)对股票市场波动率评估和分析,[2]王燕辉、王凯涛(2004)应用EGARCH分析了深圳股市的波动性。[3]国债安全性并非浑然天成,“327”国债风波仍然让人记忆犹新,国债回购风险拖累了诸多证券公司和上市公司,目前国债市场的供求失衡导致国债价格变异和利率的进一步失真,从而会引发国债市场的系统性风险。交易所国债的波动,无论对于国家,还是对机构投资者,包括个人投资者,都是一个值得关注的重要问题。
二、指标选择与数据分析
(一)指标选择
上海证券交易所的国债交易量占整个交易所市场的99%。2006年3月,上海证券交易所拥有国债现货43只,国债质押式回购9只。上证国债指数(LEB)是上证指数系列的第一只债券指数,它使我国证券市场股票、债券、基金“三位一体”的指数体系基本形成。上证国债指数是以上海证券交易所上市的所有固定利率国债为样本?按照国债发行量加权而成,每月最后一个交易日,将剩余期限不到一年的国债剔除。自2003年1月2日起对外发布,基日为2002年12月31日?基点为100点?代码为000012。上证国债指数的目的是反映我国债券市场整体变动状况?是我国债券市场价格变动的“指示器”。上证国债指数既为投资者提供了精确的投资尺度,又为产品创新夯实了基础。基于上面的分析,本文选择上证国债指数为指标来对交易所国债市场的波动进行度量。
(二)数据分析
上证国债指数的动态公布是从2003年2月24开始,数据的时间区间是从2003年2月24日到2005年12月30日,共696个数据。国债指数收益率(DLEB)是通过式(1)得到的。
DLEB=InPt-InPt-1(1)
上证国债指数走势如图1所示,波谷是2004年4月30日99.1,波峰是2005年12月10日109.73。国债收益率的图形如图2所示,可以看出在一定范围内存在剧烈波动。数据来自大智慧软件,运用Eviews分析处理。

图1 国债指数历史走势
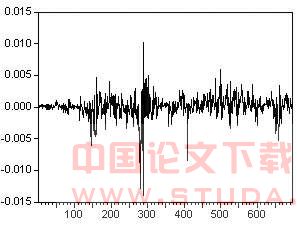
图2国债指数收益率
三、实证分析
(一)平稳性检验
采用ADF(Dickey and Fuller,1981)和PP(Phillips and Perron,1988)法进行单位根检验。对上证国债指数和收益率序列进行检验发现,国债指数序列(LEB)不是平稳序列,而收益率序列(DLEB)则是平稳性序列(见表1)。
表1 单位根检验

(二)正态性检验
国债收益的时间序列的特征是方差不仅随时间变化,而且有时变化得很激烈。对其进行正态性检验,偏度是-1.80031,峰度是17.5419,偏离正态分布的水平。按时间观察,表现出“波动集群”(volatility clustering)特征,即方差在一定时段中比较小,而在另一时段中比较大。从取值的分布看表现的则是尖峰厚尾(leptokurtosis and fat-tail)特征,即均值附近与尾区的概率值比正态分布大,而其余区域的概率比正态分布小。
对残差εt是否存在ARCH或GARCH效应进行检验,通常采用Engle(1982)提出的拉格朗日乘子检验法(Lagrange Multiplier test),简称LM检验,一般是对εt2进行AR(q)自回归估计得到拟合优度R2。然后利用结论:在不存在ARCH或GARCH的原假设下,统计量TR2服从于自由度为q的x2分布,在选定的显著性水平下,当TR2值大于x2分布的临界值时,则拒绝εt不存在ARCH或GARCH的原假设,即认为存在ARCH或GARCH效应。经过拟合,滞后1阶和滞后3阶构成的自回归时间序列比较显著。
DLEBt=β1DLEBt-1+β2DLEBt-3+εt(2)
(四)EGARCH模型
若一个平稳随机变量可以表示为AR(p)形式,其随机误差项的方差可用误差项平方的q阶分布滞后模型描述,则称为ARCH模型。为避免ARCH模型的滞后项过多,可采用加入st2的滞后项的方法,这就形成GARCH模型,即广义自回归条件异方差模型。
EGARCH模型,即指数(Exponential)模型,由Nelson在1991年提出的,其目的是为了刻画条件方差对市场中正、负干扰的反应的非对称性。[4]模型中条件方差采用了对数形式,意味着杠杆效应是指数型的。此时条件方差ht为延迟扰动项εt-i 的反对称函数:
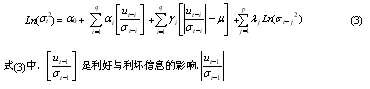
ARCH项。与GARCH和ARCH相比,这种模型的优点在于可以区别正信息和负信息的不同影响。正信息表示“利好”,负信息表示“利坏”。虽然正信息和负信息的绝对值相同,但EGARCH模型可以区别正、负信息对波动的不同影响。因此EGARCH模型可以很好的描述了市场中的非对称性。此外由于方差被表示成指数形式,因而对模型中的参数没有任何约束,这是EGARCH模型的一大优点。因为等式右侧是st2的对数,所以无论等式右侧是正是负,作为其反对数,st2总是正的。上式右侧第2项是用条件标准差st除信息ut及其滞后项,(ut /st)表示标准信息。第3项是用均值u减标准信息的绝对值。
经过分析,EGARCH(1,1)是拟合的较好的模型,即对式(2)和式(4)进行回归分析,结果如表2所示,利坏的影响强于利好信息的影响。
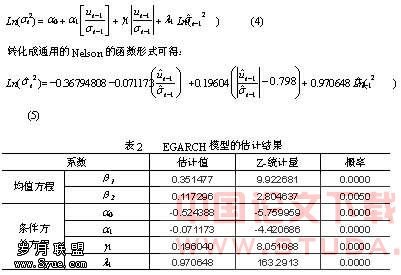
四、结论与建议
经过实证分析,交易所国债指数序列不是平稳序列,而收益率序列则是平稳性序列,分布呈现尖峰厚尾特征,收益率在一定的范围内存在波动性。值得说明的是,经拟合所得的EGARCH模型显示利坏信息的影响要远远大于利好信息的影响。
交易所国债市场的波动性原因可归结为三点:首先是国债自身的波动性,交易所国债并非一劳永逸的,其风险依然存在;其次是国债市场的分割,Granger因果关系检验发现银行间国债市场与交易所国债市场价格传递,微观结构中传染机制起到举足轻重的作用;最后是投资者行为,投资者厌恶损失,非理性行为造成羊群效应等非理性现象,增加了交易所国债市场的波动性。
2006年,交易所国债市场一路飙开,但交易量大幅萎缩,股市与债市的跷跷板效应日趋明显。勿庸置疑,国债不仅为国民提供了大量建设资金,也在一定程度上满足了社会各类投资者投资国债的需要,不断扩大的国债发行规模,为市场提供了更多的流动性,有利于活跃和稳定金融市场,保证财政政策和货币政策的有效实施。国债关系国计民生,财政部和人民银行等相关部门应实时监控、审时度势,加强国债市场基础设施建设,加强两大市场的联系机制,采用公开市场等手段,把国债的波动控制在“黄金输送点”的安全范围内。国债是机构投资者资产组合的必然选择,机构投资者应在团队研究凸性与久期等基础上,采取的投资策略。国债是个人投资者,特别是风险厌恶者,相对理想的投资工具,切勿盲目跟庄,以免遭遇巨大的风险。国债价格是社会资金供求的反映,国债收益率是基准利率的代表,我国国债市场的改革发展依然迫切。
:
[1] 唐旭.国债市场金融功能分析[J].新金融,2005,(4).
[2] 黄后川,陈浪南.中国股票市场波动率得到评估及特性分析[J].经济研究,2003,(2).
[3] 王燕辉,王凯涛.股票交易量对收益率波动性的影响——对深市各股的实证分析[J].金融研究,2004,(12).
[4] 王佳妮、李文浩.GARCH模型能否提供好的波动率预测[J].数量经济技术经济研究,2005,(6).










