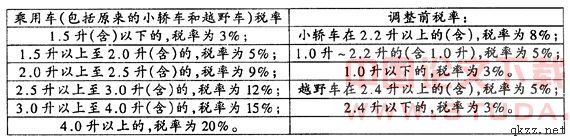
征税与纳税行为博弈关系的实证分析减少税收流失的对策选择
[摘 要]税收是国家财政收入的主要来源,如何减少税收流失是个非常严峻的问题。通过建立规范的征税机关和纳税人之间的博弈模型,基于征税机关与纳税人行为的学分析,可以得出该模型的纳什均衡解。证明了应从增大对偷税行为的惩罚力度、降低征税部门的稽查成本、提高对征税机关有效稽查的激励、降低征税机关的稽查风险等方面入手来治理偷税现象。
[关键词]税收流失;实证分析;博弈模型;纳什均衡;政策启示
一、征税与纳税行为分析的经济学基础
我国税收流失的形式和手段主要包括纳税人采用偷税、骗税、抗税、避税、欠税等手段造成的税收流失以及因税收寻租、国有资产流失、越权税式支出、行政干预、地方保护主义、费挤税等形式造成的税收流失。在这些税收流失形式中,偷税是最主要最严重的形式。
(一)纳税人偷税行为因素分析
纳税人偷税行为动因可以从内在因素与外在环境因素两方面进行分析。其一,内在因素。首先,受利益最大化心理驱使。经济学领域中最基础的是“理性经济人”假设,理性经济人在一定约束条件下总是希望实现自身利益最大化,而税收是国家无偿占有纳税人的财富,会导致纳税人经济利益的减少,这与理性经济人的内在目标相违背,所以他们千方百计企图通过偷税来实现其税后利润最大化。其次,受不平衡心理驱使。一方面税收灵活性过大和行政执法不公造成纳税人竞争环境的不平等,由此形成偷税得到更大的收益,诚实纳税反而利益受损的心理状态;另一方面,富人收入高但纳税额并不比中低阶层多,纳税使贫富差距越来越大,这也使一些纳税人心理不平衡,诱发其偷税。再次,受盲目侥幸心理驱使。税务机关受人力、物力、财力及其他各类社会因素的影响,执法力度相对偏软,导致纳税人认为国家对偷税行为的打击不会恰巧落到自己头上,而且即使偷税被抓,罚款数也远小于偷税金额,有时甚至还可采取非正常手段免于处罚,偷税成本远远小于偷税收益。其二,外在环境因素。首先,税收执法力度偏软,震慑力不足。税务执法队伍素质良莠不齐、执法不公、税收立法层次低、各级相关政府部门与税务部门相互配合不够,地方保护主义和行政干预随处可见,致使对偷税的打击力度不够,偷税罪刑罚过轻。其次,权力腐败和政府公共产品存在缺陷。权力的腐败导致纳税人心理畸形,他们认为纳税只能是助长特权和腐败的催化剂,纳税人纳税享受不着更多的公共产品和公共服务,导致其依法纳税的意识降低。
(二)税收管制市场的静态均衡模型
根据经济学中的理性经济人假设,任何一个理性纳税人都是一个“理性”的者,在实施偷税行为之前,他们会将偷税的预期成本与预期收益进行比较,从而决定是否从事偷税行为。而在现实生活中,情况并非如此。通常认为,偷税行为屡禁不止完全是因为赋税过高、惩罚不严、执法不力导致的。但会不会还有其他的因素导致纳税人偷税?下面,笔者通过建立税收法律市场中的静态均衡模型,来寻找税收管理环境中影响偷税行为的因素。
我们可以把纳税人对税收征管法律的态度当作对其他商品的偏好来看待。这样,根据纳税人对税收征管法律的选择和偏好,每个纳税人都会有一个以此来定义的效用函数。当偷税的预期效用大于纳税的预期效用时,纳税人就会选择偷税。在此,我们把纳税人的收入划分为不偷税收入和偷税收入,相应的,存在着不偷税价格和偷税价格(假定纳税者有着自己的主观估价)。在给定社会税法管制环境下,纳税主体在面临价格与收入的双重约束下,选择购买适当规模的x和y,以使自身效用最大。
假定纳税人的偏好用柯布一道格拉斯(Cobb-Douglas)效用函数的对数形式表示:u(x,y)=aLnx+bLny(a≥0,b≥1,a+b=1)
在固定收入约束条件下,纳税主体的预算约束方程为:x P+yP=M+M=M
由以上两个式子可以得出,纳税主体在偷税行为与不偷税行为之间的边际替代率为:MRS=-ay/bx=-P,/Py
显然,偷税和不偷税的边际替代率呈递减趋势,在此情形下,该纳税主体消费哪种商品,就取决于两种商品的相对价格。如果相对于不偷税,偷税的价格高,纳税主体将趋于减少对偷税的需求而更多地选择不偷税;反之亦然。
一定时期内,纳税人的素质较为稳定,纳税人对税收法律的需求不会发生剧烈变动,其需求弹性较小,相比之下,税收法律的供给则更易波动,供给弹性也较大。因此,在社会治安综合管理的过程中,应当将重点放在提供高的偷税价格上。

通过以上对纳税人行为因素及征税机关静态均衡的分析可以得知,造成税收流失现状的因素来自于多方面,主要有税收法律市场中的执法和司法变量、纳税人偷税价格等方面。纳税主体想要偷税,征税机关要惩罚偷税行为,于是就出现了纳税人与征税机关之间针锋相对的局面。这种情形下,将纳税人与征税机关作为一个博弈模型的双方进行分析,可以帮助我们以一个新的方式去认识关于税收征管环境中的法律知识,寻求到造成偷税行为的关键性因素,从而找出防止税收流失的途径。
二、纳税人与征税机关之间利益博弈的实证分析
(一)模型的假设
1 局中人--博弈过程中独立决策、独立承担后果的个人和组织。根据利益的一致性,可将局中人设为两方:一方是按照法律规定,应当按时交纳税收的纳税人;另一方是代表政府执法部门的征税机关。为了使得表述更为简洁,在模型的求解过程中,用G代表征税机关,用T代表纳税人。
2 信息--博弈者所掌握的对选择策略有帮助的情报资料。即纳税人知晓征税机关何时稽查及惩罚力度,征税机关知晓纳税人是否偷税及偷税金额等等。

3 策略--博弈方可选择的全部行为或策略的集合。纳税人为了获得最大利益,会根据“成本一收益”的比较,选择以下两种策略:依法按时交纳规定数额的税款(简称不偷税)和不缴纳税款(简称偷税)。征税机关为了追求税收收入的最大化,其选择的策略也有两种:对纳税人进行稽查(简称稽查)和不对纳税人进行稽查(简称不稽查)。策略假设的前提是:纳税人和征税机关对其策略组合的选择都必须避免性,否则一旦对方发现,则会根据这种规律性预先猜到对方先前采取的策略并采取针对性的策略而始终获益。所以,本模型中的两个局中人应随机化自己的可选策略,即采取混合策略而非纯策略。
4 次序--博弈参加者做出策略选择的先后顺序。在此假定纳税人优先选择其策略组合,即是否偷税,随后征税机关选择其策略组合,即是否稽查。
5 支付--博弈双方的收益。即各博弈方做出决策选择后的所得与所失。纳税人和征税机关对双方要付出的成本及其收益都非常清楚。纳税人选择偷税,会给他带来预期收益;当然,若偷税被征税机关查出,则纳税人将面临一定的惩罚;并且,每个纳税人均通晓税收法规,知道自己的应纳税额、何时纳税、逃税会受到什么惩罚。而征税机关对纳税人进行稽查,需要花费大量的人力和财力,通过稽查,偷税可能被查出,但受征税机关稽查人员素质、纳税人精心设计假账等主客观因素的制约;偷税也可能查不出来,此时,征税机关将遭受一定的损失。
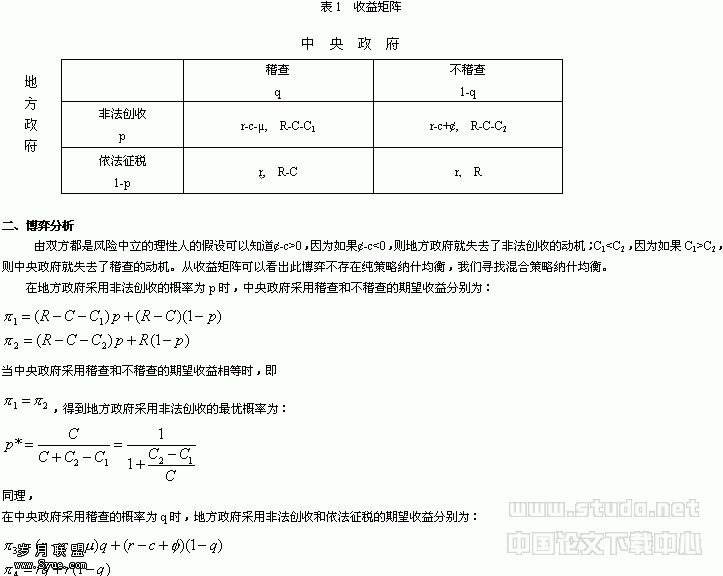
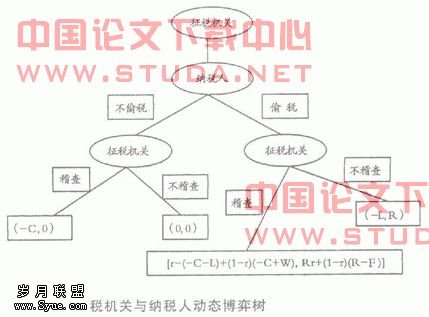
征税机关与纳税人之间博弈过程如下:第一回合:征税机关根据税收法规,要求纳税人按照规定纳税,纳税人处于选择点。如果纳税人选择不偷税,对于纳税人来说,纳税是他应尽的义务,其损益状况为0。这时,若征税机关选择稽查,它将损失稽查成本,其损益状况为-c;若征税机关选择不稽查,它将节约稽查成本,其损益状况为0。第二回合:若上一回合中,纳税人选择偷税,此时,征税机关处于选择点。它可以接受纳税人的偷税而选择不稽查,在这种情况下,纳税人由于偷税而获得额外收益R,而征税机关由于未将偷税行为查出来,损失了-L。但是,如果征税机关选择稽查,则双方博弈进入下一回合。第三回合:征税机关不认可偷税而选择稽查并对偷税行为进行处罚,则纳税人不仅要按章纳税,还要承担由于偷税而带来的处罚。由于征税机关稽查的风险为r,根据数学期望的概念,可以出征税机关支付的期望值为r(-C-L)+(1-r)(-c+w)和纳税人支付的期望值为Rr+(1-r)(R-F)。征税机关的这个决定对双方都具有最后约束力,博弈到此结束。
可以用直观的博弈树来描述上述的征税机关和纳税人之间完美信息动态博弈的过程(如图1)。综合以上分析,我们可以得出本博弈模型的支付矩阵(如图2所示)。
用二维向量s=(sg,sl)表述征税部门和纳税人的一种对局,称为一个策略组合。为了使本模型更加合理、更加贴近实际,有必要先理顺有关变量之间的大小关系,在此,采用逆向递推法寻找各变量之间的合理数学关系:(1)若第三回合中,征税机关采取稽查将获得损益r(-c-L)+(1-r)(-c+w),如果r(-c-L)+(1-r)(-c+w)≤-L,即(1-r)w-r L-c≤-L,也就是说,征税机关选择稽查行为所获得的收益小于选择不稽查行为所获得的收益,那么,征税机关将回到第二回合的策略,选择不稽查以获得更高的收益。纳税人也知道这种情况的存在,偷税就是其最佳选择,于是本博弈最完美的方案就是:征税机关不稽查,纳税人偷税,即S=(Sg,sl)=(不稽查,偷税)=(0,1),博弈在第二回合结束。但是,这种情形在现实生活中比较罕见,为了使模型的分析结果具有现实意义,应当假设(1-r)W-rL-C>-Lo(2)若第-回合中,纳税人选择偷税将获得损益Rr+(1-r)(R-F),如果Rr+(1-r)(R-F)≤0,即R≤(1-r)F,也就是说,在知道征税机关在一定的概率水平下会稽查的前提下,纳税人偷税所获得的收益不能超过其将要面临的处罚时,纳税人是没有偷税的动力的,他在第一回合中就会选择不偷税,于是本博弈最完美的方案就是:纳税人不偷税,征税机关不稽查,即s=(sg,sl)=(不稽查,不偷税):(0,0)。但现实生活中纳税人偷税的现象仍然普遍存在,为了使模型更加能说明问题,应当假设R>(1一r)F。(3)根据国家规定的财政收支两条线原则,可以假设w与F无直接关系,即纳税人偷税所受到的处罚,同征税机关稽查成功获利并没有直接的相关关系。
(二)模型的建立
在以上的博弈分析过程中,预先设定纳税人和征税机关对博弈的过程都非常了解。但这样的完美信息组合在现实生活中是不存在的,因为偷税具有隐蔽性和欺骗性,征税机关在一般情形下很难知道纳税人是否完全纳税、是否存在偷税。既然征税机关不可能完全知晓纳税人的先前选择,征税机关和纳税人之间的博弈在现实中就不可能是完美信息动态博弈,而只能是静态博弈。
尽管本博弈的两个局中人在现实社会中并不清楚各种对局情况下对方甚至自己的得益,但为了进行理论上的探讨,暂且假定他们是相互熟知的,即本博弈模型为完全信息静态博弈。由于本博弈模型的两个局中人都是在给定信息的情况下,以某种概率分布随机地选择自己不同的策略,因此,不存在同时实现双方利益最大化的最佳策略组合,本博弈不存在纯策略的纳什均衡解,而只可能是混合策略的纳什均衡解,征税机关及纳税人都不会始终采用同一种策略,只有这样,二者才有可能实现利益最大化。
传统上,学的所有研究都是基于“理性经济人”假设的。然而,现实生活中人们的行为模式很难符合“理性经济人”假设;也就是说,“理性经济人”很难看成是对现实社会的合理近似。因此,在任何一个博弈模型中,每个局中人都有一定的犯错误的可能性。这种局中人在理性条件下不该选择却选择了的情况,便偏离了均衡策略,在博弈论中称为“颤抖手精炼均衡”。本文直接引用了泽尔腾(Reinhard selten)的证明结果及证明过程,作为颤抖手均衡的正式定义。
泽尔腾将这种局中人发生错误选择的情况形象地称为“颤抖”,当某个局中人使得理性条件下不该发生的事件发生时,这个不该选择的选择行为视为此局中人的非蓄意失误。由于局中人的“手”(策略选择)可能“颤抖”(偏离纳什均衡的要求),致使其策略集中的每一个纯策略都有被选中的可能,即每个纯策略被选中的概率都严格为正。原博弈的均衡,可理解为被“颤抖”扰动后的博弈均衡的极限。
本博弈中,纳税人和征税机关都可能发生在理性条件下本不应发生的非蓄意失误。例如,纳税人本不应该偷税却选择了偷税,征税机关本应该稽查却因人力、财力的限制而做出不稽查的决策。所以,严格意义上来说,本博弈模型应当属于一个“颤抖手精炼均衡”。化简后的支付矩阵如图3所示。
可以预见,左上方的策略组合(稽查,偷税)=(Sg,sl),其中,Sg=(p,l-p):(1,0),st:(q,l-q):(1,0),即[(1-r)w-r L-c,R-(1-r)F]是本模型的混合策略的纳什均衡解,且为颤抖手精炼均衡解。因为从理论与现实的角度出发,如果纳税人不偷税,那么征税机关就失去了存在的意义,因此,右下方的策略组合(不稽查,不偷税)绝对不会是该博弈模型的混合策略的纳什均衡解。
(三)模型的求解
根据经济学中偏导数的意义,可以求出本博弈模型的混合策略纳什均衡解。
1 对纳税人预期收益的分析。由以上分析可知,纳税人的预期期望收益函数为:
Elit=pq[R-(1-r)F]+(1-p)qR+0+0=q[R-(1-r)pF]
对上式取一阶导数,则纳税人的最优化条件为:a(EU)/aq=R-(1-r)pF=0
因此,征税机关稽查的均衡概率为:p0=R/(1-r)F
由预期期望收益可知,当R-(1-r)pF>0,即p
从人员配备上看,税务系统税务稽查人员比率不到10%,税务检查概率低是显而易见的。由于各方面的原因,在我们的实际操作过程中,对于有偷税行为的纳税人,有相当大一部分并未完全按照《税收征管法》的规定予以处罚,仅仅追回了税款。此时,F=0,p0=1,而现实生活中,税务机关的检查率不可能达到100%,这种情况所产生的后果就是:纳税人将百分之百地选择偷税。
因此,纳税人选择偷税或不偷税取决于税务机关进行检查的概率和对偷税行为的处罚力度,即税务机关检查的概率越高,对偷税行为的处罚力度越大,纳税人偷税的可能性就越小;反之则越大。
2 对征税机关预期收益的分析。由以上分析可知,征税机关的预期期望收益函数为:
EUg=pq[(1-r)w-rL-c]+p(1-q)(-c)+(1-p)q(-L)+0=p[(1-r)q(w+L)-C]-qL
对上式取一阶导数,则征税机关的最优化条件为:a(EU)/ap=(1-r)q(w+L)-C=0
因此,纳税人偷税的均衡概率为:q0=C,(1-r)(w+L)
由预期期望收益可知,当(1-r)q(w+L)-c>0,即q>q。时,为了使得预期收益尽可能大,征税机关应当选择p=1,即始终选择稽查作为其最优策略;当(1-r)q(w+L)-C<0,即q
3 征税机关和纳税人博弈模型的混合策略纳什均衡解。通过以上数学计算,本文得到了本博弈模型的纳什均衡解(p0,q0)=[(R/(1-r)F,c/(1-r)(w+L)]。也就是说,当纳税人以概率q0选择偷税且征税机关以概率p0进行稽查时,本博弈模型刚好达到纳什均衡,并且是一个颤抖手精练的纳什均衡。
三、博弈模型的政策启示
根据以上博弈模型的纳什均衡解(p0,q0),我们可以采取相应措施来防范纳税人的偷税行为。要遏制纳税人的偷税行为,就必须尽可能降低q0;而征税机关所付出的成本要受到国家财政预算约束,同时,作为国家行政机关,若始终采用稽查策略,就意味着对纳税人的不信任,不利于社会的稳定和,因此,应尽量降低p0。
由于po=R/(1-r)F,q0=c/(1-r)(w+L),要降低po、q0的数值,必须找出能控制的自变量,通过实施适当的控制,从而达到降低p0、q。的目的。通过观察并结合现实情况,可以发现,真正可以控制的变量有F和w,在一定程度上可以控制的变量有c和r,而对于R和L是很难以控制的。因此,只有合理控制F和w,尽量控制C和r,才能更好地减小p0、q0。具体包括:
1 增大F,增加偷税行为的价格,即增大对偷税行为的惩罚力度。从p0=R/(1-r)F可以看出,要减小p0的值,在假定R和r不变的前提条件下,只有增大F,即通过加大对偷税行为的惩罚力度,提高罚金数量,才可以有效地降低稽查概率并减少偷税行为。从总体上看,我国对偷税行为的处罚力度较低,现有的法律规定很难起到对偷税行为强有力的威慑作用和制裁作用。因而,我国有必要加大对偷税行为的惩罚力度,根据经济发展状况,提高罚款数额。
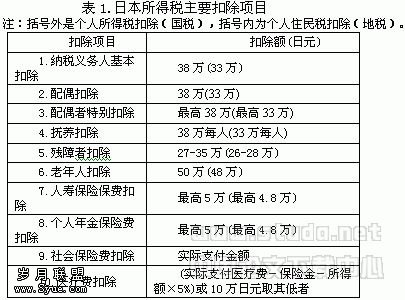
同时,我国“有关规定的灵活性太大,在执行过程中还大打折扣”。根据《税收征收管理法》六十三条的规定,我国对偷税行为的处罚力度在50%到50倍之间,其间跨越幅度较大,而且没有明确规定在什么情况下必须采用较高的处罚力度,也没有明确规定在何种情形下可以对偷税者采用较低的处罚标准,这无形中赋予税务稽查机关很大的自由裁量权,使得稽查人员在某种程度上可以依据自己的偏好对不同的偷税人采用不同的处罚标准。虽然自由裁量权是行使职权所必须的,但过分的自由裁量权则容易导致权利寻租①,间接地降低偷税行为的风险。因而,要有效地防止偷税行为,除了应加大对偷税行为的惩罚力度、还必须限制征税机关的自由裁量权,使处罚力度、等级更为明确,消除纳税人的侥幸心理,增加罚金对偷税者产生的心里震撼力。
此外,建议对我国现行的《刑法》和《税收征收管理法》予以修订,提高偷税罪的量刑标准,以提高对欲偷税者的警示作用和对偷税者的打击力度;对每一次偷税行为的处罚都给偷税人造成极大震慑,使得纳税人不敢偷税。
2 提高w,降低c,即适当增加征税机关的预算,在降低征税部门的稽查成本的同时,提高对征税机关有效稽查的激励。由q。=c/(1-r)(W+L),可以看出,在假定r、L不变的前提条件下,要减小q0的值,只有按一定比例增大w的值,降低c的值。由于w是纳税人偷税且被查出能给征税机关带来的收益,所以,可以采取给稽查有功人员增发奖金等表彰奖励措施,来激发监管部门稽查的主观能动性。同时,应通过征税部门加强自身管理、进一步完善税收征收稽查制度、普及纳税知识以提高全民的纳税意识等途径,切实降低稽查成本。
要有效减少偷税行为,稽查概率也就必须维持在一定的水平之上。现阶段,征税机关的稽查成本有限,而且税务稽查人员所占的比重不足。面对纳税人偷税成本低且法律惩罚力度不高的环境,国家为了减少税收流失,在一定程度上还需要加大对稽查成本的投入,发展稽查队伍,提高稽查概率。但应当注意的是,稽查成本过高,将会得不偿失,甚至会刺激偷税行为。因而,我国应当根据不同情形,计算所应当投入的稽查成本。
3 降低r,即降低征税机关的稽查风险。从p0=R/(1-r)F和q0=c/(1-r)(w+L)可以看出,通过降低r的值,可以很好地实现同时降低q0及p0的目标。降低征税机关的稽查风险,就是提高征税机关稽查的准确率,通过稽查,使得纳税人偷税行为充分暴露。现实生活中,可以通过提高稽查人员的业务水平,进一步降低税收制度中存在的某些不确定性等措施,来降低稽查风险。当然,要完全消除。是不现实的,因为现实中,在努力降低稽查风险的同时,往往会伴随着稽查成本的升高。所以,我们必须努力在降低稽查风险和降低稽查成本之间做出权衡。
此外,强化纳税人的纳税意识、优化法律制度和管理机制、严厉打击政府工作人员违法犯罪行为、国家不断为纳税人提供便利条件、建立税收信用制度等均能在一定的程度上减少偷税行为的发生。
以上所得出的结论毕竟是在博弈分析的基础上得出的,在建立博弈模型的时候,本身就提出了一系列的假设,它不可能囊括现实生活中的方方面面,一些影响纳税行为的因素可能未在此博弈模型中体现出来。例如,静态博弈模型中,提出了信息相对完整的假设,但在现实中信息却是不完备的。因而,促使信息更加完备也是国家减少偷税行为所必须考虑的问题。
虽然现阶段我国的偷税现象较为严重,但是只要征税机关的税务稽查概率选择得当,同时对全社会进行积极的人生观价值观,进而树立依法纳税的观念,优化税收秩序、营造全社会积极、健康的纳税心态和税收环境,必能扭转我国税收流失严重的局面。