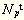积极财政政策宏观经济效益分析——基于宏观计量模型的研究(上)
1、引言
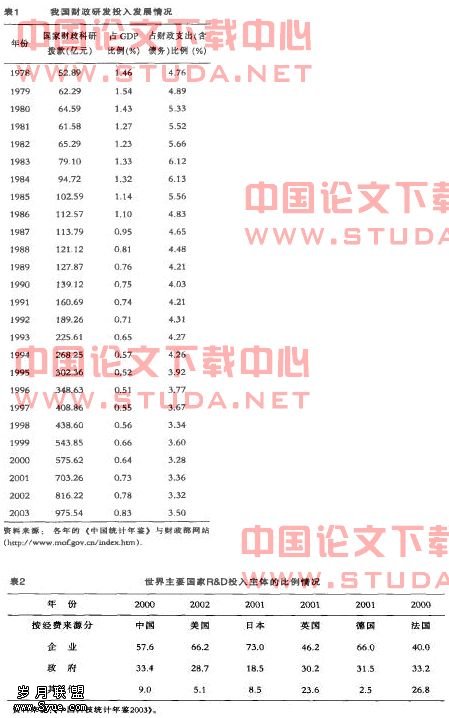
在1997年开始出现了的通货紧缩,为此国家动用了积极的财政政策。从1998年到2002年期间,中国政府每年大约发行了2000个亿以上的国债,这些国债大多用于基础建设的投资。毫无疑问积极财政政策的实施为我国在2003年底彻底走出通货紧缩的阴影作出了不可磨灭的贡献。与此同时,由国债投资所建成的一大批基础设施,也为我国未来保持长期高速增长提供了坚实的基础。
国内关于积极财政政策宏观经济效益的研究从积极财政政策开始实施时刻起就一直在进行。国家社会基金、国家科学基金、国家软科学研究计划、财政部有关部门以及一些地方和单位为此设立了许多研究项目,有关的研究、报告和著作更是数不胜数。然而,许多研究是以理论研究和定性分析为主,缺少准确的数据支持和缺少建立在经济数学模型基础上的定量分析。与此同时,几乎所有的研究都是集中在积极财政政策对需求的拉动上,而很少考虑积极财政政策所形成的一大批基础设施对提升整个国家经济整体实力(或生产能力)的作用。
本文将通过一个宏观计量模型来研究积极财政政策的宏观经济效益。与传统模型所不同的是,我们的模型不仅考虑了需求,同时也引入了社会的供给能力。从而,它不仅区别于建立在一般均衡基础上的以供给为核心的新古典模型(如实际商业周期模型等),同时也区别于传统凯恩斯类型的总需求模型(如IS-LM和AS-AD模型等)。尽管如此,这样一种模型本质上仍然是具有凯恩斯特点的非均衡模型。由于中国所具有的转型经济和中国家的特点,这种具有凯恩斯特点的宏观经济模型更适合于对中国经济的研究。
本文结构安排如下:第二部分构筑宏观模型,第三部分为模型的估计,第四部分为积极财政政策的宏观经济效益分析,最后第五部分是一个简单的。
2、宏观经济模型
我们将首先建立一个简单的单部门宏观经济模型。该模型将为我们评估积极财政政策提供一个统一的框架。正如我们所指出的,该模型是一个具有许多凯恩斯特点的非均衡模型。这种非均衡性不仅表现在劳动力市场和产品市场上,与此同时,价格对非均衡的调整也具有滞后和黏性。
总供给(或总产出)
令Yt代表实际总产出(即实际GDP),Ydt代表实际总需求,总产出与总需求之间的差额为实际存货Vt的变化。于是我们有
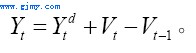 (1)
(1)
(1)式表明存货Vt是按其t期的期末值衡量。有理由相信,总产出Yt是由预期的总需求Yet决定。经过存货纠正后,总产出Yt可表示为:
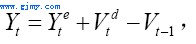 (2)
(2)
以上,Vdt为理想的库存水平,Vdt-Vt-1可以理解为库存纠正量。如果预期Yet能够实现,即Ydt=Yet,则由公式(1)和公式(2),我们得到Vt=Vdt,即t期的期末存货等于其理想的存货。关于理想的库存水平Vdt,我们假定它与Yet满足线性关系:
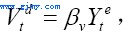 (3)
(3)
其中,参数βv>0。
接下来我们分析总需求的预期Ye是如何决定的。一个更符合实际的假设是厂商期望的是经济(或实际GDP)的增长率get。这样,通过对增长率的预期,我们可以测算出厂商的总需求预期。按照预期的适应性调整规则(the rule of adaptive expectation),我们有:
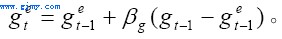 (4)
(4)
其中,参数βg>0。
总生产能力
需要说明的是,通常按生产函数所给出的产量只能理解为一个社会的总生产能力。我们设该生产能力为Ypt。由于中国仍然是一个发展中国家,而发展中国家的一个特点是经济的二元结构和与此相对应的无限的劳动力供给,因此在中国当前经济条件下,生产能力不受劳动力供给的制约,而完全由资本存量所决定。这种资本和劳动力之间的不可替代性表明生产函数是Leontief型而不是Cobb-Dauglass型,即
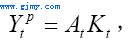 (5)
(5)
这里,Kt为t期的资本存量,At为产量-资本比(可理解为资本生产力)。显然,按照等式(2.5)所给出的生产函数,At的上升反映了技术的进步,即同样的资本投入能创造出更多的生产能力。给定生产能力Ypt,生产能力利用率Ut就可以写成
 (6)
(6)
此外,资本存量Kt服从如下累积:
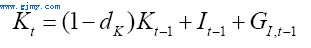 (7)
(7)
以上,It−1为投资;GI,t-1为政府投资;dK为折旧率。需要注意的是,按照公式(7),我们并没有区分政府资本和企业资本。这主要是由于我们没有相关的数据。
接下来,我们将考查技术At的决定因素。根据Romer(1990),技术是人类思想和知识的凝聚。具体的说,技术可以表现为各种论文、专著、设计和专利等。由于技术是非竞争的,即一项技术可以同时被不同的人和企业使用,因此技术存量的提高通常意味着要素生产力的提高。令技术存量的提高为At-At-1,按照Romer(1990),我们有
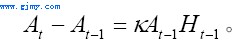
该公式表明技术存量的提高取决于现有的技术存量At−1和用于科研的人力资本Ht−1。由于经验数据表明At−1和Ht-1对新技术的产生具有某种程度的边际递减效应,因此Jone(1995)和Gong,Greiner and Semmler(2004)分别对上述公式进行了修正。按照后者
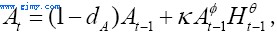 (8)
(8)
以上,φ,θ
和Ad都为(0,1)区间上的参数,其中dA可以理解为技术或知识的折旧率。
总需求
按照定义,t期国内产品的实际总需求Ydt可以表示为
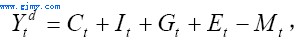 (9)
(9)
其中,Ct表示消费;It表示(包括外资企业)投资;Gt是政府支出;Et是出口;Mt是进口。所有变量都为实际值。其中对于消费函数,我们采用如下简单形式:
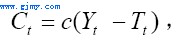 (10)
(10)
这里,参数c∈(0,1)为边际和平均消费倾向;Tt表示税收;Yt−Tt可以被看成是家庭在t期的可支配收入。
对于投资函数,我们假定:
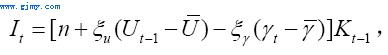 (11)
(11)
以上,参数ξu和ξγ都为正值;γt为实际利率; 分别为Ut和γt的稳定状态(由各自的样本均值衡量)。这样,
分别为Ut和γt的稳定状态(由各自的样本均值衡量)。这样,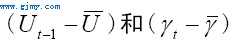 分别表示Ut-1和γt对于它们各自稳定状态的偏离。该公式表明,投资是为了创造生产能力,因此,当生产能力紧缺时(由较高的Ut−1反映),投资较高,反之也然。与此同时,投资也取决于融资成本(这里由利率γt反映)。在另一篇文章中,作者使用货币供给增长率来代替(11)式中的利率,并提供了相应微观基础的讨论。我们想说明的是,此两种类型的投资方程并不冲突。这里,我们只需假设利率和货币供给增长率是密切相关,而这也和的宏观调控实践相一致。有关讨论随后展开。
分别表示Ut-1和γt对于它们各自稳定状态的偏离。该公式表明,投资是为了创造生产能力,因此,当生产能力紧缺时(由较高的Ut−1反映),投资较高,反之也然。与此同时,投资也取决于融资成本(这里由利率γt反映)。在另一篇文章中,作者使用货币供给增长率来代替(11)式中的利率,并提供了相应微观基础的讨论。我们想说明的是,此两种类型的投资方程并不冲突。这里,我们只需假设利率和货币供给增长率是密切相关,而这也和的宏观调控实践相一致。有关讨论随后展开。
与消费函数相对应,我们假定进口Mt与实际总产出Yt成线性关系:
Mt=mYt (12)
以上,参数m∈(0,1)为边际进口倾向。
最后,对于总需求中的其他变量Gt和Et,我们都假定它们为外生变量。
劳动力市场
我们现在考查劳动力市场。根据标准的凯恩斯理论,劳动力的需求Ldt由产量Yt决定。因此,
Ldt =ltYt (13)
以上,lt可被看作是劳动生产率,它取决于生产技术。与生产函数(5)中的At相类似,我们同样允许劳动生产率可随时间而变化。
假定劳动力供给Lst为外生变量。于是,给定劳动力供给Lst和劳动力需求Ldt,就业率Nt由如下方程给出:
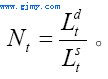 (14)
(14)
可以预见,相对於劳动力需求而言,劳动力的供给是绝对过分的,而这将影响我们的工资公式。
价格与工资
现在我们考查价格与工资的决定。我们首先假定价格和工资会对产品市场和劳动力市场的非均衡进行调整。然而,价格的这种调整是有黏性的,即价格的调整既不及时,也不会一步到位,这也同时意味着市场在大多数情况下是不能出清的。按照被广泛讨论的双重菲利普斯曲线(参见Fair 2000和Flaschel, Gong and emmler 2001),我们可以把价格和工资的动态变化写成如下形式:
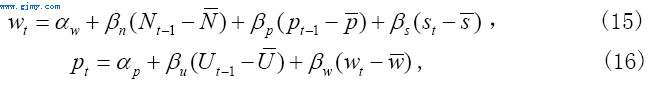
以上,pt为通货膨胀率;wt为名义工资增长率;st可理解成t期的供给冲击,它可能包含生产率的变化和进口产品的价格变化等。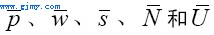 分别为变量pt、wt、st、Nt和Ut的稳定状态。当实际的Nt和Ut超过
分别为变量pt、wt、st、Nt和Ut的稳定状态。当实际的Nt和Ut超过 ,工资和价格的增长pt和wt将被加速。显然,上述价格−工资模型是建立在相当对称的有关价格和工资浮动原因的假设上。一方面价格和工资的增长来源于需求或市场的非均衡压力(分别由
,工资和价格的增长pt和wt将被加速。显然,上述价格−工资模型是建立在相当对称的有关价格和工资浮动原因的假设上。一方面价格和工资的增长来源于需求或市场的非均衡压力(分别由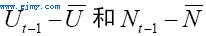 代表);另一方面,它们同时也被成本所拉动(分别由
代表);另一方面,它们同时也被成本所拉动(分别由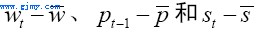 衡量)。
衡量)。
部门和货币政策
当前,中国的宏观调控手段是多种多样的。就货币政策而言,我国的货币当局不仅采用了货币供给(体现为一系列的贷款计划),同时也使用了利率作为其执行货币政策的手段。事实上,这两种手段通常会同时使用(或双管齐下)。例如当不景气时,不仅货币供给量会增加,同时利率也会下跌。由于我们在公式(11)中只引入了利率作为投资融资的约束条件,因此,我们这里只需考虑利用类似于Taylor规则(Taylor,1993)的如下利率方程来反映我国的货币政策对中国宏观经济的影响:
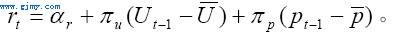 (17)
(17)
以上公式表明,利率对生产能力利用率和通货膨胀率作出反应。此外,给定名义利率rt,实际γt则可以近似的写成:
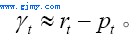 (18)
(18)
3、模型的估计
接下来我们将讨论如何估计模型中的各项
结构参数。首先需要说明的是,我们不可能也没有必要对模型中的所有参数同时进行估计。该模型包括很多预期和其他难以观察的变量,比如Yet、Ypt和At等。尽管很多方程式是线性的,但是方程中按一般线性方法所能估计的参数通常是多个结构参数的某种组合。这就导致了估计中可能产生的非线性问题。因此,在这种情况下,只要有可能,我们将逐一的利用单个方程对模型中的结构参数进行估计。此种方法经常被用于估计多变量和多等式的大型宏观经济模型。参见Flaschel,Gong and Semmler (2001,2002)等