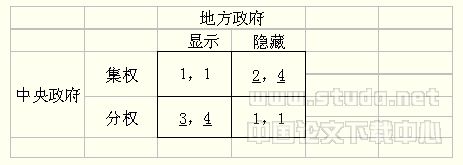
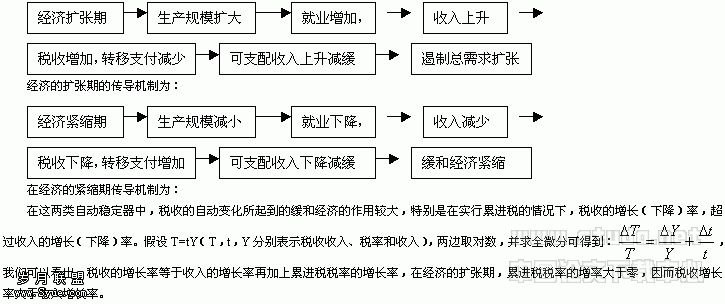
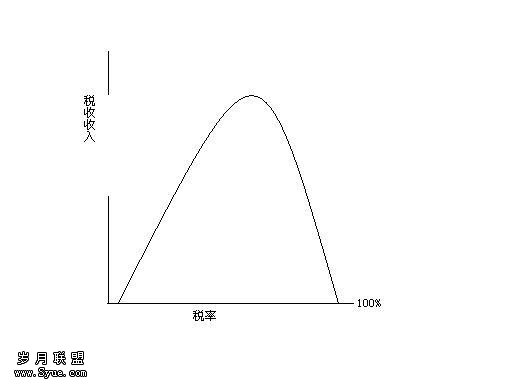
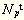积极财政政策宏观经济效益分析——基于宏观计量模型的研究(下)
参数估计和方差报告
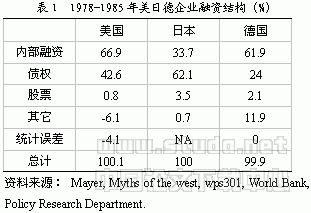
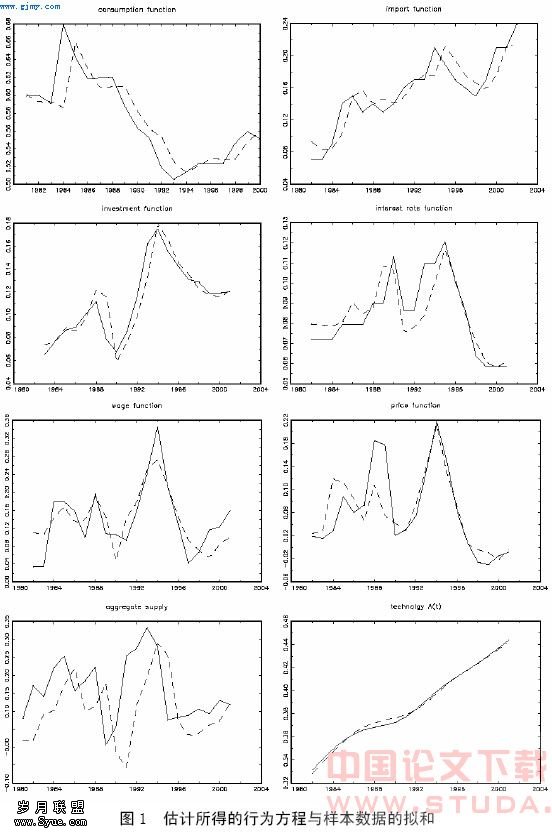
我们把所有的结构参数分为9个组。表1列出了它们的估计值和标准差。图1则给出了估计所得的行为方程与样本数据的拟和。所有数据都是年度数据。由于样本数据有限,我们的参数估计并不能完全尽如人意。接下来我们将解释表1中的估计值是如何得到的。

3-9 组的参数估计
我们的讨论首先从第9组开始。我们发现9组中的参数大多可解释为样本平均值或定义在只有一个结构参数的方程中。这就允许我们使用一阶距的方法(method of first moments)对它们进行估计。
尽管一阶矩方法能同样用于估计消费函数(10)和进口函数(12)中的参数c和m,然而我们发现其结果并不令人满意。为此我们允许c和m能随时间而变化。我们假设

其中,ct≡Ct/(Yt-1-Tt-1);mt≡Mt/Yt;vt和εt都假设为独立同分布(i.i.d.)的正态随机变量。这表示边际消费和进口倾向都服从于一阶自回归AR(1)过程。将公式(20)和(22)分别代入(19)和(21),我们得到

其中,c0=c(1−ρ),c1=ρ,m0=m(1−λ),m1=λ。现在我们可以用最小二乘法(OLS)对上述方程进行估计。而有关的结构参数c、m、ρ和λ则由下列公式获得:

需要说明的是,此种方法无法使我们直接得到参数c等的估计方差。为此我们必须把该估计看成是非线性估计。这样,我们就可以使用Judge et. al (1988,p508-510)所讨论的方法来求解参数估计值c等的标准差。在这一过程中,我们利用GAUSS语言中的GRARDP程序来计算有关的一阶导数矩阵。该矩阵被用于推导参数估计值的协方差矩阵。
对于投资函数(5)中的参数估计,我们采用如下估计方程:
 (25)
(25)
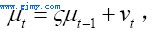 (26)
(26)
其中,it=It/Kt-1;vt同样为独立同分布的正态随机变量。这里我们所采用的估计方法为Cochrane-Orcutt方法
此外,在对工资、价格和利率方程(15)-(17)进行估计时,我们假定方程中所有的干扰项都为服从独立同分布的正态随机变量。这样,我们就可以直接利用普通的最小二乘法对它们进行估计。
需要说明的是,在我们对工资公式(15)进行估计时,我们用劳动生产率(实
际GDP与就业之比)来代表供给冲击,即解释变量st。与此同时,我们发现参数βn的估计值极不显著,因此,我们令它为0。这也同时意味着劳动力市场的供求状态对工资没有任何影响,或者说,在劳动力市场一直是处於供过于求的状态。劳动力市场的这种供过于求反映了由中国二元结构所造成的大量剩余劳动力的存在。
总供给的参数估计
对于产出方程(1)-(4)中的结构参数βv和βg的估计则更为困难。首先,我们无法得到期望值get和Yet;其次,尽管我们可以从方程(1)中推算出ΔVt,但是,我们并没有存货Vt的数据(这需要有一个存货的初始值)。为了避免使用数据Vt,我们的估计需要建立在对方程(2)进行一阶差分的基础上。与此同时,利用(3)对Vdt进行置换,我们得到
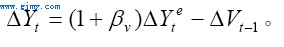 (27)
(27)
按照预期增长率get的定义,我们有ΔYet=getYdt-1。将其代入公式(27),我们可以得到参数βv的估计方程:
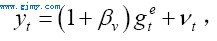 (28)
(28)
其中
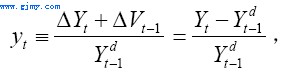
以上,误差项νt同样被假定为服从独立同分布的正态随机变量。
显然,对于βv的估计需要获得时间序列get,该数值我们无法得到。然而给出参数βg和get的初始值ge0,我们能从(4)中推算出get。假定ge0=g0,也即预期
增长率get的初始值等于其实际的观察值。设立目标函数:
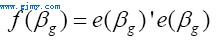 (29)
(29)
这里,e(βg)是在给定的βg情况下,对方程(28)进行线性回归所得的误差向量。这样f(βg)就可以看成是该误差的平方和。由此,对于参数βv和
βg的估计可以看成是寻找一个βg使得目标函数f(βg)最小。这里,我们使用搜索法来实
行这一最优化过程。
技术函数中的参数估计
需要说明的是,上述估计过程中所使用的数据大多可以从国家统计年鉴中获得,资本存量Kt则来源于张军(2003)。然而,对於技术函数中的参数dA、φ和θ的估计,我们首先需要解决无法观测的变量At和Ypt的数据来源问题。如果我们假定生产用电力消耗与资本设备的实际使用成线性相关,则通过利用生产用电力消耗数据,我们就能测算出At和Ypt。假定一定时期内生产用电力消耗和资本服务使用量成固定比例,也即
St=hEt (30)
其中,St为资本服务的使用量,即St=UtKt;Et为生产用电量;h为一个正实数。给定St及公式(5)和(6),相应的实际产出则可由下式导出:
Yt=AtSt (31)
进一步将(30)代入(31),我们得到
St=AthEt (32)
对(32)式两边分别求对数并进行差分,我们可得到
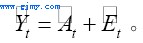 (33)
(33)
以上 分别表示为产出、技术和用电量的对数差分(近似于它们的增长率)
分别表示为产出、技术和用电量的对数差分(近似于它们的增长率)
由于Yt和Et都是已知的,由公式(33)我们可以算出At,再进一步由(32)解得h。给定h,我们可以按公式(30)求得资本服务量St,并进而按定义St=UtKt导出Ut。给定Ut和At,我们可以进一步通过公式(6)测算出Ypt。
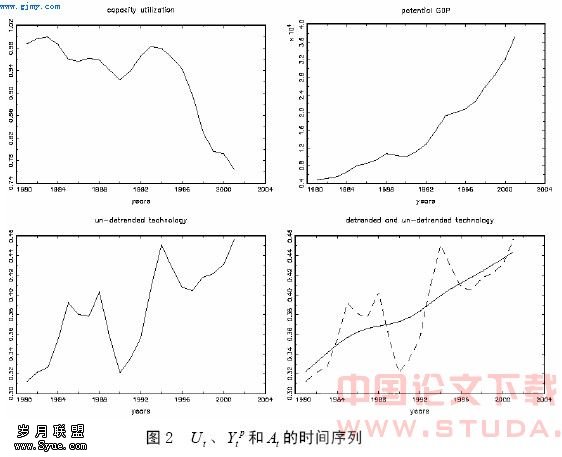
需要说明的是,在按公式(32)求解h时,我们需要的是At,而我们从(33)式中得到的则是其增长率At。因此我们必须有个基年(这里采用1980年)的资本生产率A0。现假定基年的资本设备利用率为100%,则A0可由公式A0=Y0/K0求得。图2 给出了我们所测算出的Ut、Ypt和At的时间序列。
图2
需要说明的是,由此而测算出的技术存量At具有较大的波动,甚至会出现技术退步。显然此种情况与我们所想象的实际有所不同。我们可以想象技术总是在不断进步,技术的存量也在不断增加,而且这种增加应是一个平缓的过程,不应出现大起大落。显然,这种过分的波动来源于各种误差干扰(如我们所假定的用电量与资本服务量之间线性关系中所出现的误差)。因此,我们有必要对图2中C格的At进行滤波(或光滑)处理,经过滤波以后的At由图2中的D格所示。
给定数据At,我们就可估计技术函数(8)中的结构参数dA、φ和θ。然而,在此之前,我们仍然要对公式(8)的H作一番解释。按照Romer(1990)的原意,H为用于科研的人力资本。然而,除了现有的技术存量和人力资本的投入外,技术的提高也有赖于科研所需的物质投入和有效的激励机制。研究需要设备和经费,而有效的激励机制(如专利制度和对贡献的奖励制度等)对技术进步的作用也是显而易见的。因此,如果我们使用国内现有的数据,H可以看成是国家用于和科研的投入。
估计所采用的方法仍然是最小二乘法,即使误差平方之和为最小。然而由于方程所体现的非线型性,我们必须采用一种全局数值优化(global optimizationalgorithm)的方法对参数进行估计。在这一研究中,我们所采用的是模拟淬火(simulated annealing)法。
4、积极财政政策宏观效益分析
接下来,我们将利用我们所估计的模型分析和测算过去5年(1998-2002)积极财政政策给我国经济带来的影响。测算所依据的原则是“有无原则”(with andwithout principle)。这一原则在项目评估时经常被使用。按照这一原则,我们分别在“有”和“无”积极财政政策条件下我们所关心的各项经济指标,如GDP增长率,通货膨胀率和就业率等。比较这些指标的不同就能使我们测算积极财政政策的宏观经济效益。
无论是“有”还是“无”,我们都必须通过对模型的模拟,计算出有关的宏
观经济指标。关于这一模拟,我们要求:
所有外生变量都用实际样本值来表示;
所有随机变量的实现值都用模型估计时所留下的残差来表示;
所有内生变量都由模型的模拟计算得到。
假设过去5年里没有积极(或扩张性)的财政政策,政府支出应等于税收。因此,所谓没有(或无)积极财政政策的条件是:令过去5年里每年的政府支出等于其当年的税收。与此同时,我们还必须考虑到在没有积极财政政策条件下,政府的支出结构也有可能发生变化。为此,我们使用国债投资中的支出结构来推算在没有积极财政政策情况下的支出结构。表2给出了这一推算。
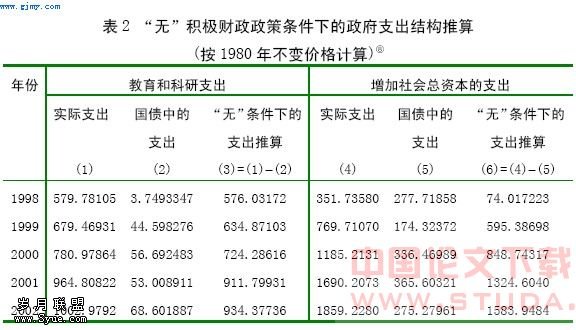
需要说明的是,尽管对于“无”积极财政政策的情况,我们有理由使用对模型的模拟计算出有关的宏观经济指标,然而,为什么对于“有”积极财政政策的情况,我们不能直接使用实际的样本观察值来代表相关的经济指标?由于模型的参数估计和设定本身也有可能产生误差,因此,即使我们引入了误差项的实现值和实际的外生变量,当我们对模型进行模拟时,仍然有可能使模型的模拟值与样本值有偏离。为了使由模型的参数估计和模型的设定等原因所引起的误差对评估的影响减少到最少,我们对于在“有”积极财政政策条件下的经济指标的测量与“无”积极财政政策条件相似,即都通过对模型的模拟算出,两者的不同仅仅体现在政府支出的总量和结构上。
表3 给出了过去5年积极财政政策宏观经济效益的评估。
首先,我们需要说的是,这里的财政赤子与国债支出并非完全相同。当政府的支出大于其税收时,它仍然可以动用除发行国债之外的其它资源,如过去的财政积余等,来弥补其支出。
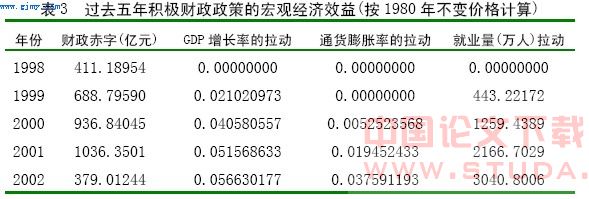
其次,按照我们所构造的模型,政府的支出无论从供给或需求角度看,它对经济的影响都有一定的滞后。因此,98年的积极财政政策对98的国民经济并没有什么影响。当然这里并不意味着现实中这种影响就不存在。如果我们的模型是以季度(或月度)为一期进行估计,此种影响显然就可以得到反映。
第三,表中所反映的拉动效应是一种累积效果。以2002年的GDP增长率拉动0.056630177为例,该数据表明,假如没有1998-2001年的积极财政政策,则2002年的实际GDP将减少5.6630177个百分点。按照这一思路,2001年的积极财政政策给2002年GDP的拉动效应为5.6630177-5.1568633≈0.5个百分点。尽管与前期积极财政政策的拉动效应相比,这一效应似乎在递减。然而,我们也应同时看到,它在创造2002年的就业机会上的贡献并没有过分减弱。
5、结束语
本文利用了一个简单的宏观计量模型对1998-2002年期间积极财政政策的宏观经济效益进行了测算。研究表明积极财政政策的实施为我国在2003年底彻底走出通货紧缩的阴影作出了不可磨灭的贡献。而到了2002年,积极财政政策的拉动效应也已递减,这也此后逐渐淡出的积极财政政策提供了一定的依据。由于目前积极财政政策已经淡出,因此本文的意义更多的在于其理论和技术应用的研究,希望本文能够抛砖引玉,对未来我国宏观经济政策的研究(特别是定量分析)有所启发和借鉴。

其次,按照我们所构造的模型,政府的支出无论从供给或需求角度看,它对经济的影响都有一定的滞后。因此,98年的积极财政政策对98的国民经济并没有什么影响。当然这里并不意味着现实中这种影响就不存在。如果我们的模型是以季度(或月度)为一期进行估计,此种影响显然就可以得到反映。
第三,表中所反映的拉动效应是一种累积效果。以2002年的GDP增长率拉动0.056630177为例,该数据表明,假如没有1998-2001年的积极财政政策,则2002年的实际GDP将减少5.6630177个百分点。按照这一思路,2001年的积极财政政策给2002年GDP的拉动效应为5.6630177-5.1568633≈0.5个百分点。尽管与前期积极财政政策的拉动效应相比,这一效应似乎在递减。然而,我们也应同时看到,它在创造2002年的就业机会上的贡献并没有过分减弱。
5、结束语
本文利用了一个简单的宏观计量模型对1998-2002年期间积极财政政策的宏观经济效益进行了测算。研究表明积极财政政策的实施为我国在2003年底彻底走出通货紧缩的阴影作出了不可磨灭的贡献。而到了2002年,积极财政政策的拉动效应也已递减,这也此后逐渐淡出的积极财政政策提供了一定的依据。由于目前积极财政政策已经淡出,因此本文的意义更多的在于其理论和技术应用的研究,希望本文能够抛砖引玉,对未来我国宏观经济政策的研究(特别是定量分析)有所启发和借鉴。