基于流感疫苗改装研究（一）

                                     作者：梁绮莹　马海超　张一辰

　　关键词：自回归移动平均模型　扩散权重　聚类分析　优先级系数

　　论文摘要：本文就病毒亚型分布与爆发情况，以及流感监测分布概况进行了分析，探讨了疫苗改装、下一年优势毒株的可能分布区域与需援助国家的优先级问题。

　　由地理区域相似性将全球划分成七个区域，根据每个区域 、 、 、 四种病毒亚型爆发情况与人口比重进行权值求得每种病毒亚型的扩散权重，然后引入ARIMA(自回归移动平均模型)对数据进行统计分析，得到每种病毒亚型在每个地区的独立扰动值，进而预测出每种病毒亚型在各区域流行季节中所占比重，依此可得改装疫苗的投放方案（表 4-2）。对于疫苗改装的可行性，我们引进覆盖率的标准进行了评价。（表）

　　通过对七个区域病毒亚型扩散权重的计算与分析，我们发现对于流行毒株种类的变更主要出现在冬季的后期，而对于下一年威胁较大的病毒可能出现在北美洲和亚洲地区。

　　通过引入聚类分析中的分层聚类，对193个国家根据其卫生支出占GDP百分比聚类，将其分成8个类别（表4-4）。通过计算国家优先级系数 ，确定需援助国家优先级。系数 越大，国家优先级越高，越需要联合国经费援助。

　　一、问题重述

　　流感是一种广泛流行于世界范围内的疾病，每次流感大流行都会造成多人死亡和巨大损失。世界卫生组织大力推荐将疫苗作为一种有效的预防措施来抗击这种潜在的致命性疾病。如果疫苗毒株1和流行的病毒类型相匹配，那么大约有50%-80%的疫苗接种者能够抵抗流感的侵袭。即使疫苗不能完全抵御流感的侵袭，它也可以降低流感发病的严重程度以及严重并发症的发生率。但流感疫苗所能产生的抗体是短效的，所以每年流感流行季节到来前，都需要重新接种疫苗。每年冬天是流感的流行季节，在流行季节到来前1-2个月接种疫苗，能达到较为良好的防护效果。

　　流感病毒分为A、B、C型。A型病毒容易发生变异，根据抗原不同可区分不用亚种，B型病毒变异缓慢，C型病毒甚少对人类造成威胁。对于病毒变异的多样性和变异性，每年采用疫苗的成分不同世界卫生组织专家痛过对全球疫情的监控来收集数据，在每年二月份预测新的流行季节中流感流行情况，并确定毒株品种作为新年度北半球流感疫苗的推荐成分。需要给药品制造商留出半年左右的时间以生产和投放市场。现在管用的推荐方案是三联装一面，也就是每份疫苗中有三种经过灭活或裂解处理的毒株，分别问两个A型和一个B型。

　　根据流感传播、构成、变异与疫苗市场建立模型解决以下问题：

　　【问题1】：降低流感疫苗的制造成本，将三联装的流感疫苗改装成双联装。将北半球和南半球分别划分成稍小的区域，并使用不同的疫苗针对不同的区域来投放，请建立的模型，设计一个可行的投放方案，并设计一个评估标准来评估其效果，使之能与现行方案进行对比评价。

　　【问题2】：考虑选择具体毒株，评估和预测对下一年威胁性最大的病毒品种。建立合理的模型，在流感流行记录中，筛选出对下一年威胁较大的病毒出现的区域。

　　【问题3】：流感病毒依靠多种途径传播。一旦出现流行，就难以预测和控制其最终的流行范围和持续时间。所以为了控制流感的传播，需要有快速反应的应对措施。世界卫生组织 (WHO) 在世界范围内建立了流感监测网络。包括世界流感中心及实验室，国家级流感中心，数量众多的国家级流感监测网络实验室和哨点。流感监测网络的作用是监视流感在全球的活动情况，并且及时准确地将流感爆发的信息、病毒分离的结果上报世界卫生组织，进行病毒的研究鉴定。为了提高流感监测网络的覆盖率和反应能力，一方面需要提高各级流感中心对病毒样本的研究鉴定能力，另一个很重要的方面是需要增加基层投入，主要包括流感监测网络实验室和哨点医院的数量。假设联合国有部分经费可以援助不同国家，用以建设流感监测网络实验室和哨点医院。请依据数据，建立合理的模型，评估需要援助的国家或地区的优先级。

　　二、符号说明与问题假设

　　2.1 符号说明：

　　2.1.1 问题一、二的符号说明

　　2.1.2 问题三的符号说明

　　2.2 问题假设：

　　1、假设所收集的流感病毒资料真实有效。

　　2、假设A型病毒在研究区域与时段中分为H1、H3和其余总和三种亚型。

　　3、假设B型病毒在研究区域与时段中不发生变异，不存在亚种。

　　4、假设C型病毒在研究区域与时段中对人类不造成威胁。

　　5、假设全球按北美洲、南美洲、欧洲、亚洲、北非、撒哈拉以南非洲沙漠、大洋洲区域划分。

　　三、问题分析

　　3.1 问题一的分析

　　流感的预防与控制可通过在人体内接种疫苗类预防性生物制品方式达到目的，然而疫苗的造价高昂，需要依随病毒的变异而不断更新变化等因素的影响，使流感的预防与控制难度进一步加大。为疫苗的推广进一步普及，目前的三联装疫苗可根据病毒的地域性分布差异而改进成二联装疫苗。

　　对于病毒的地域性分布的相似性，我们将全球分为北美洲、南美洲、欧洲、亚洲、北非、撒哈拉以南非洲沙漠、大洋洲七大区域，对世界卫生组织流感监测项目资料中2007年3月至2008年2月数据进行如下分析：

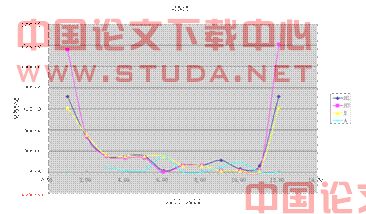
图3-1   北美洲2007.3-2008.2

　　1)      北美洲

　　位于北半球，冬季为流感高发期，通过对数据的统计分析，绘制图像可以得到右图。图中可以明显看出在当年的12月至次年的3月，是流行性感冒的高发期。在高发期中H3、H1两种病毒有明显优势。我们通过此变化曲线预测其满足ARIMA(Auto-regressive Integrated Moving Average Model),即自回归移动平均模型。

　　2)      北非

　　位于北半球地中海沿岸，气候，地形与欧洲有一定的相似性，但由于其地形特殊和人口密度小等原因，全年基本不存在流感高峰期，也不具有北半球流感爆发的特性，故在以下模型分析中暂时将其忽略不具体考察。

　　欧洲为北半球的典型模型，流感爆发时间集中，在该年的12月至次年的4月，然而其爆发期中 、 、 三种病毒扩散权值差值较小，在三联装改进成二联装是需要利用模型求解。

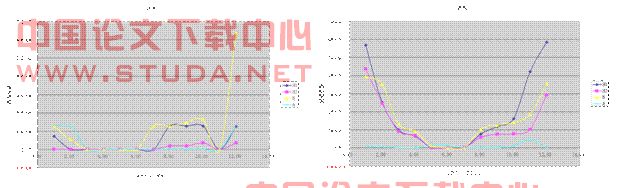
　　　　　　　图 3-2  北非2007.3-2008.2                                                               图3-3 欧洲2007.3-2008.2

　　3)      亚洲

　　亚洲因人数为全世界之首，其流感的影响程度大，持续时间长，而在不同时期内不同病毒的存活的差异亦相对北半球其余各州大。在模型的研究中重点的疫苗改装问题可通过病毒扩散权值因子的差异来选择适合二联装疫苗的组成。通过数值变化得到变化函数，从而推断明年的疫苗选择。

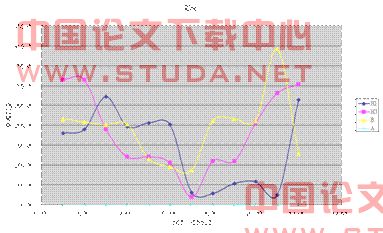
图3-4 亚洲2007.3-2008.2

　　4)      南美洲和撒哈拉以南非洲

　　南美洲和撒哈拉以南非洲位于东西半球相同的纬度之上流感的爆发有一定的相似性，在该年的5月到8月为高峰期，可用上述模型分析。

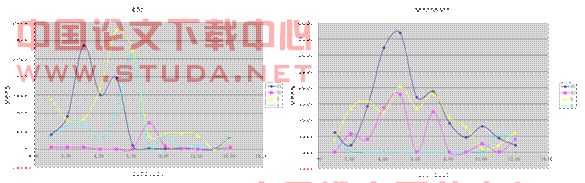
　　　　　　　图3-5 南美洲2007.3-2008.2                                           图3-6 撒哈拉以南非洲2007.3-2008.2

　　5)      大洋洲

　　大洋洲位于印度洋与太平洋间，人口集中且相对其他大陆较少，能收集的相关系数亦不多，在图中可分析H3、B两种显著地病毒。不将其作为南半球主要模型，只通过其往年数据推断明年疫苗情况。

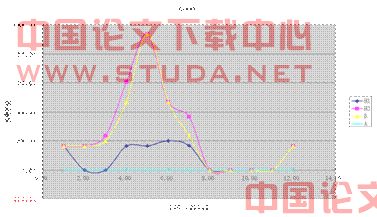
图3-7 大洋洲2007.3-2008.2

　　3.2 问题二的分析

　　问题二主要讨论优势毒株的选择问题。在问题一中我们从众多病毒亚型中选取最典型的四种亚型种类。由资料可得，亚型中可以根据其发现地点、时间进行编号，而成为不同的毒株。

　　对于评估和预测下一年的优势毒株，对2001-2008年这7年的数据进行分析，并根据权值计算公式计算出各个区域内4中病毒亚型的权值，再将它乘以每个区域人口占世界总人口的百分比得到全球范围内的各病毒亚型所占百分比。

　　以2007.3-2008.2的实例画出的全球范围的病毒亚型百分比如下图饼状图所示，其中蓝色表示亚型、褐色表示亚型、绿色表示亚型而紫色则表示为亚型所占的比例。

图3-8 全球 2007.3-2008.2病毒亚型比例

　　四、模型的建立与求解

　　4.1 问题一模型的建立与求解

    为解决以下问题，于此引入ARIMA(Autoregressive Integrated Moving Average Model),即自回归移动平均模型。模型的定义如下：

　　在全球流感监控组织所提供的2007年3月至2009年1月全球流感季节性分布内容与种类的数据中，包含世界各大洲人口主要分布国家在全年中不同月份不同病毒的爆发情况。病毒的爆发程度分为四个等级：偶然性爆发、当地爆发、区域性爆发和大范围爆发，其严重性与传播性以指数型性增长，我们近似认为，爆发程度每上升一级，其扩散权重因子就增加一倍，即为2的指数幂的函数关系。

　　将所有数据进行处理后得到了流感病毒中主要分类 、 、 、随时间的序列分布，一组依赖于时间t的随机变量，而这组随机变量具有自相关性表征预测对象的延续性。以下引入ARIMA(Autoregressive Integrated Moving Average Model),即自回归移动平均模型，通过从时间序列的过去值及现在值可以预测其未来值。

　　应用以上模型，对数据分析处理有如下三方面：1.数据平稳化预处理；2.模型的识别定阶与模型参数估计；3.模型的诊断检验。

　　4.1. 1数据平稳化预处理

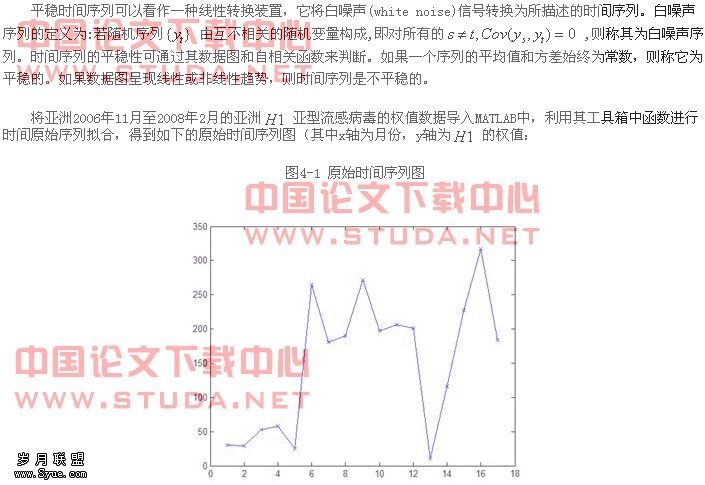
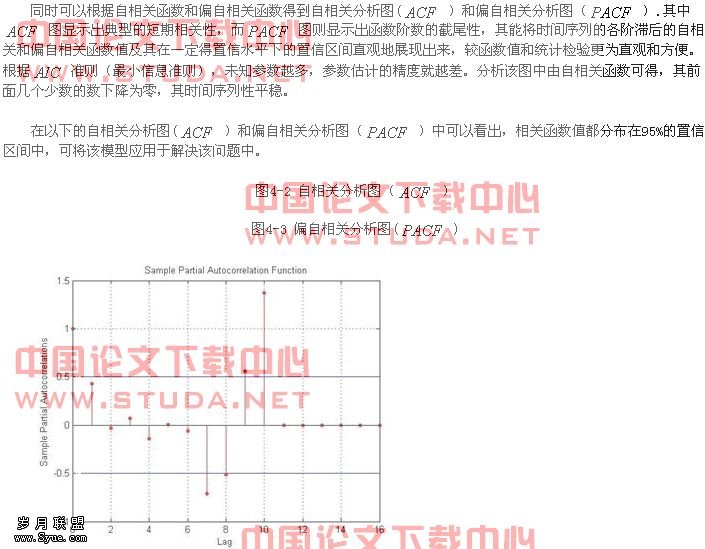
　　4.1. 2模型的识别定阶与模型参数估计

　　4.1.3 模型的诊断检验

　　模型的适合程度，需要对其拟合优度进行检验，典型方法是对观测值和弄醒的拟合值的残差进行分析。如果残差序列不是白噪声序列，则说明还有信息包含在相关的残差序列中未被提取，则此时可对残差拟合更复杂的模型以达到更适合的情况。

表 4-1  模型中的残差诊断

Residual Diagnostics