基于流感疫苗改装研究（二）
4.1.2 问题一模型的结果
4.1.2.1 模型结果的得出
根据上述数据分析，光滑曲线散点图对2007.3-2008.2时间段的描述，根据
模型中所求得的独立扰动值，可以出每个地区每种病毒在当地流行的比重，双联装装疫苗的成分则取比重较大的两种亚型作为疫苗成分，用其来预测2008.10-2009.1的数据，与2008.10-2009.1的实际数据相比较，在误差允许范围之内，模型具有可行性。模型预测的三联装改进为二联装在全球的七大区域方案如下：
表 4-2全球冬季疫苗改装预测
预测 | 区域 | 双联装中所包含的亚型 |
北半球 (2008.10-2009.01) | 北非 |
|
北美洲 |
| |
亚洲 |
| |
欧洲 |
| |
南半球（2008.04-2008.07） | 撒哈拉以南非洲 |
|
南美洲 |
| |
大洋洲 |
|
4.1.2.2 模型结果的诊断检验
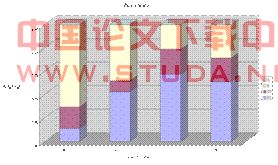
根据以上方法，在南北半球各选取典型区域进行一下诊断检验，经数据验证可得该序列为白噪声序列，且据2008.10-2009.1的南非实际流感病毒的数据，我们可以得到如下图4-4的柱状图，其中青色表示示
,黄色表示,
紫红色表示
，蓝色表示
,在
轴上对应的比例便是该病毒在四种病毒中所占的比重。我们通过2007.3-2008.2的数据作为既得的原始数据，而通过模型求解可以求得2008.10-2009.1的数据，从而检验模型的正确性。
根据以上分析数据，算法设计，公式假设，函数导出，可得到如下右图4-5的柱状图。在图中可清晰看到，两者数据基本一致，模型具有可行性，可用于预测2009年冬季流感高峰期双联装疫苗的选择使用。
南半球
图 4-6 南非（实际）与南非（预测）
附：
北半球
图 4-7 欧洲（实际）与 欧洲（预测）
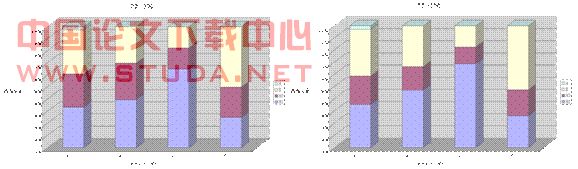
4.2 问题二的模型建立与求解
4.2.1 问题二模型的建立
对于评估和预测下一年的优势毒株，对2001-2008年这7年的数据进行分析，并根据权值计算公式计算出各个区域内病毒亚型的权值，再将它乘以每个区域人口占世界总人口的百分比得到全球范围内的各病毒亚型所占百分比。
对世界范围内第
种病毒扩散权重：
(其中
为区域编号, 
为国家编号, 为病毒编号,)
以下利用聚类分析的方法对于既得的病毒的权重进行分析。
聚类分析是指在所选变量的基础上对样本数据进行分类，分类结果是各个变量综合计量的结果，以个体间的距离来度量个体间的“亲疏程度”。对于个体间的“亲疏程度”的度量一般有两个角度：一是个体间的相似程度，在问题二中，我们将国家作为个体，而在地理区域上相邻的国家在人种、医疗水平、状况等因素上相似，我们可以对于这些国家进行聚类，从而简化问题；二是个体间的差异程度，而个体间的差异程度通常用距离来测度。距离是指将每个样品看成是
个变量在维空间中的一个点，然后在该空间中所定义，距离越近则紧密程度越高。通过对记得的数据进行聚类分析，我们可以得到下一年威胁较大的病毒所处位置的最大可能性，以便于专家的研究和疫苗的生产与投放。
4.2.2 问题二模型的求解
由数据可以发现对于流行毒株种类的变更主要出现在流行季节的后期，所以当其用于估计与预测下一年的优势毒株时，需要重点关注流感高发区域——北美洲和亚洲，重点时间段（北半球当年的12月与下一年1，2月）的毒株分离情况，对其中的毒株加以研究就可以准确预测出下一年流行季节的优势毒株而确定出下一年的疫苗成份。
图4-8 北美洲与亚洲2007.3-2008.2病毒亚型比例
北美洲 亚洲
4.3 问题三的模型与求解
4.3.1 聚类分析原理与模型
4.3.1.1 聚类分析原理
聚类分析（cluster analysis）,是多元统计学中应用极为广泛的一类重要方法。为解决以下问题，我们引入聚类分析中的分层聚类的分析方法。应用分层聚类Q型聚类对样本进行聚类，即将具有相似的样本聚集在一起，使差异大的样本分离开来。
就分层聚类法的聚类方式而言，可以分为凝聚方式聚类和分解方式聚类。在解决该问题中，我们采用的是凝聚方式聚类，其过程是：首先将
个国家看出类（一类包括一个国家），然后将性质最接近的两类合并成一类(性质接近一般指距离接近)，从而得到
类；接着从中找出最接近的来那个两类加以合并变成
类。重复这一过程，直到所有的国家都在一类当中。可见，在凝聚方式聚类过程中，随着聚类的进行，类内的“亲密”程度在逐渐降低，对个国家通过步可以凝聚成一大类。
在分层聚类中涉及对于个体间“亲疏程度”的度量和对于小类间“亲密程度”的度量。个体间“亲密程度”的度量，则可以先定义国家与小类、小类与小类之间的距离，距离小的关系比较密切，距离大的关系比较弱。
4.3.1.2 聚类分析数学模型
据世界卫生组织报告中可得，世界上共有193个与世界卫生组织建立合作的国家，而某些国家在国家经济条件，医疗水平等方面有一定的相似性，可以根据其相关参数的相近性对国家进行聚类。我们假设第个国家卫生支出占GDP的百分比为
，对其进行分层聚类， 在193个国家中选取具有代表性的20个国家的的值导入SPSS软件中，可以得到分层聚类中的凝聚状态表如下，此表中给出了系统聚类过程中的聚类信息，即每一个类被合并的类、被合并类间的类间距离以及最终的类水平。
表 4-3 分层聚类中的凝聚状态表
Agglomeration Schedule
Stage | Cluster Combined | Coefficients | Stage Cluster First Appears | Next Stage | |||
| Cluster 1 | Cluster 2 | Cluster 1 | Cluster 2 | Cluster 1 | Cluster 2 |
|
1 | 12 | 19 | .000 | 0 | 0 | 4 | |
2 | 9 | 16 | .000 | 0 | 0 | 8 | |
3 | 8 | 20 | .010 | 0 | 0 | 10 | |
4 | 11 | 12 | .010 | 0 | 1 | 5 | |
5 | 1 | 11 | .020 | 0 | 4 | 13 | |
6 | 4 | 18 | .040 | 0 | 0 | 9 | |
7 | 6 | 10 | .040 | 0 | 0 | 14 | |
8 | 7 | 9 | .040 | 0 | 2 | 11 | |
9 | 4 | 13 | .170 | 6 | 0 | 12 | |
10 | 3 | 8 | .305 | 0 | 3 | 13 | |
11 | 5 | 7 | .703 | 0 | 8 | 14 | |
12 | 2 | 4 | .977 | 0 | 9 | 15 | |
13 | 1 | 3 | 1.008 | 5 | 10 | 17 | |
14 | 5 | 6 | 1.302 | 11 | 7 | 17 | |
15 | 2 | 17 | 1.832 | 12 | 0 | 18 | |
16 | 14 | 15 | 5.760 | 0 | 0 | 19 | |
17 | 1 | 5 | 6.225 | 13 | 14 | 18 | |
18 | 1 | 2 | 19.867 | 17 | 15 | 19 | |
19 | 1 | 14 | 103.914 | 18 | 16 | 0 | |
在表4-3中，第一列（Stage）表示聚类分析的步数；第二列，第三列（Cluster Combined）表示这一步聚类中哪两个国家或小类聚成一类；第四列（Coefficients）是国家距离或小类聚类；第五列和第六列（Stage Cluster First Appear）表示这一步聚类中参与聚类的是国家还是小类，0表示国家，非0表示由第 步聚类生成的小类参与本步聚类；第七列（Next Stage）表示本步聚类的结果将在以下第几步中用到。
同时生成分层聚类的树状图如下：
图 4-9 分层聚类树状图
在图4-9中，树形图以躺倒树的形式展现聚类分析中的每一次合并的情况。SPSS自动将各类间的距离映射在0-25间，并将聚类过程近似地表示在图上，在图上可以很清晰地看到聚类的过程。
将上述步骤应用到193个国家上，就可以得到其相应的凝聚状态表、冰柱图和树状图。最终可以将193个国家划分成8类，具体划分情况如下表所示：
表 4-4 193个国家经分层聚类后类型一览表
类 | 阿尔及利亚 | 类 | 萨摩亚 | 类 | 安道尔 | 类 | 阿尔巴尼亚 |
安提瓜巴布达 | 沙特阿拉伯 | 澳大利亚 | 巴巴多斯 | ||||
亚美尼亚 | 塞拉利昂 | 巴哈马 | 白俄罗斯 | ||||
阿塞拜疆 | 新加坡 | 博茨瓦纳 | 玻利维亚 | ||||
巴林 | 所罗门群岛 | 巴西 | 布隆迪 | ||||
孟加拉国 | 斯里兰卡 | 保加利亚 | 柬埔寨 | ||||
伯利兹 | 苏丹 | 布隆迪 | 塞浦路斯 | ||||
贝宁 | 阿拉伯叙利亚 | 哥伦比亚 | 捷克共和国 | ||||
不丹 | 塔吉克斯坦 | 哥斯达黎加 | 刚果民主 | ||||
喀麦隆 | 泰国 | 克罗地亚 | 吉布提 | ||||
佛得角 | 汤加 | 古巴 | 多米尼克 | ||||
中非共和国 | 特立尼达多巴哥 | 芬兰 | 多米尼加 | ||||
乍得 | 突尼斯 | 格鲁吉亚 | 埃及 | ||||
智利 | 土耳其 | 海地 | 萨尔瓦多 | ||||
土库曼斯坦 | 匈牙利 | 格林纳达 | |||||
科摩罗 | 乌兹别克斯坦 | 爱尔兰 | 几内亚 | ||||
库克群岛 | 瓦努阿图 | 以色列 | 几内亚比绍 | ||||
科特迪瓦 | 委内瑞拉 | 日本 | 圭亚那 | ||||
朝鲜 | 也门 | 黎巴嫩 | 洪都拉斯 | ||||
厄瓜多尔 | 类 | 阿富汗 | 卢森堡 | 伊朗 | |||
厄立特里亚 | 阿根廷 | 马尔代夫 | 吉尔吉斯坦 | ||||
爱沙尼亚 | 奥地利 | 马耳他 | 拉脱维亚 | ||||
埃塞俄比亚 | 比利时 | 黑山 | 莱索托 | ||||
斐济 | 波斯尼亚 | 挪威 | 立陶宛 | ||||
加蓬 | 加拿大 | 巴拿马 | 马里 | ||||
冈比亚 | 丹麦 | 巴拉圭 | 墨西哥 | ||||
加纳 | 法国 | 圣马力诺 | 蒙古 | ||||
危地马拉 | 德国 | 塞尔维亚 | 尼日尔 | ||||
印度 | 希腊 | 斯洛伐克 | 波兰 | ||||
伊拉克 | 冰岛 | 斯洛文尼亚 | 大韩民国 | ||||
牙买加 | 意大利 | 南非 | 圣基茨 | ||||
哈萨克斯坦 | 约旦 | 西班牙 | 圣卢西亚 | ||||
肯尼亚 | 荷兰 | 马其顿共和国 | 圣文森特 | ||||
老挝 | 新西兰 | 乌干达 | 圣多美 | ||||
利比里亚 | 尼加拉瓜 | 北爱尔兰 | 塞内加尔 | ||||
马达加斯加 | 帕劳 | 乌拉圭 | 塞舌尔 | ||||
马来西亚 | 葡萄牙 | 类 | , , 安哥拉 | 苏里南 | |||
毛里求斯 | 摩尔多瓦 | 文莱达鲁萨兰 | 斯威士兰 | ||||
摩纳哥 | 卢旺达 | 刚果 | 多哥 | ||||
摩洛哥 | 瑞典 | 赤道几内亚 | 乌克兰 | ||||
莫桑比克 | 瑞士 | 印度尼西亚 | 坦桑尼亚 | ||||
纳米比亚 | 图瓦卢 | 科威特 | 越南 | ||||
尼泊尔 | 津巴布韦 | 阿拉伯利比亚 | 赞比亚 | ||||
尼日利亚 | 类 | 基里巴斯 | 毛里塔尼亚 |
| |||
巴布亚 | 马拉维 | 缅甸 | |||||
秘鲁 | 马绍尔群岛 | 阿曼 | |||||
菲律宾 | 密克罗尼西亚 | 巴基斯坦 | |||||
卡塔尔 | 瑙鲁 | 阿联酋 | |||||
罗马尼亚 | 纽埃 | 类别六 | 索马里 | ||||
俄罗斯联邦 | 美利坚合众国 | 类别七 | 东帝汶 | ||||
五、模型的评价
模型一的目的在于降低疫苗的制造成本，将三联装的疫苗改装成双联装，如此设想主要在于两方面考虑：一是对于某些地区，盛行并造成大规模影响的病毒只有两种，三联装疫苗造成上的浪费；二是对于某些病毒，其生命周期短，环境适应力低，疫苗对其作用不大。以下引进覆盖率的概念来评价改装的价值：覆盖率表示疫苗抵抗病毒占总病毒的百分比。表中三联装疫苗的覆盖率与双联装疫苗的覆盖率相比较，差值均在33.3%以下，可见改装后疫苗与原疫苗相比有一定的进步。
表 4-2疫苗覆盖率比较
月份 | 原三联装疫苗对病毒亚型的覆盖率 | 改装后双联装疫苗对病毒亚型的覆盖率 | |
撒哈拉以南非洲 | 4 | 100.00% | 81.31% |
5 | 100.00% | 90.53% | |
6 | 100.00% | 78.53% | |
7 | 100.00% | 79.69% | |
北美洲 | 10 | 99.02% | 75.95% |
11 | 100.00% | 80.68% | |
12 | 100.00% | 86.28% | |
1 | 100.00% | 78.90% | |
欧洲 | 10 | 89.78% | 73.81% |
11 | 96.42% | 71.45% | |
12 | 97.16% | 82.13% | |
1 | 98.23% | 84.50% |
六、模型的推广
6.1 疫苗生产预测
根据上述模型的分析与研究，我们可以看到在不同区域不同病毒亚型的流行情况，根据这些情况，我们运用问题一模型中的权值确定该地区该种亚型的权值，权值越大，证明该种亚种在该地区的爆发与流行的可能性就越大，因此在生产疫苗时就因在控制成本的前提下选用针对该种病毒亚型的疫苗。
通过2007.3-2009.1月的所有数据，我们可以预测出下一年度流感爆发的高峰期的病毒亚型比重情况，为疫苗的研制提供有效的数据。北半球与南半球数据分别如下:
表 5-1北半球数据
区域 | 病毒亚型 | 时间 | |||||||
2009.10 | 2009.11 | 2009.12 | 2010.01 | ||||||
权值 | 百分比 | 权值 | 百分比 | 权值 | 百分比 | 权值 | 百分比 | ||
北非 | H1 | 127.84 | 100% | 127.84 | 83% | 127.84 | 51% | 127.03 | 35% |
H3 | 0.00 | 0% | 26.38 | 17% | 54.24 | 22% | 36.58 | 10% | |
B | 0.00 | 0% | 0.00 | 0% | 68.86 | 27% | 200.00 | 55% | |
A | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | |
北美洲 | H1 | 158.64 | 30% | 200.00 | 37% | 561.55 | 65% | 318.27 | 41% |
H3 | 162.54 | 30% | 182.26 | 34% | 169.24 | 20% | 156.31 | 20% | |
B | 200.00 | 37% | 151.85 | 28% | 132.16 | 15% | 303.70 | 39% | |
A | 15.29 | 3% | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | |
亚洲 | H1 | 129.24 | 39% | 203.45 | 40% | 287.64 | 45% | 193.84 | 38% |
H3 | 83.56 | 25% | 109.04 | 22% | 142.24 | 22% | 179.54 | 36% | |
B | 115.37 | 35% | 191.23 | 38% | 204.89 | 32% | 132.34 | 26% | |
A | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | |
欧洲 | H1 | 83.21 | 28% | 111.29 | 24% | 216.56 | 25% | 239.88 | 20% |
H3 | 97.34 | 32% | 186.51 | 40% | 518.12 | 59% | 798.23 | 66% | |
B | 107.22 | 36% | 157.34 | 34% | 142.56 | 16% | 178.24 | 15% | |
A | 13.18 | 4% | 5.68 | 1% | 2.16 | 0% | 0.00 | 0% | |
根据上述数据，我们可以得到北半球冬季二联装疫苗成分的预测：
表 5-2北半球预测
预测 | 区域 | 双连装中所包含的亚型 |
北半球 (2008.10-2009.01) | 北非 |
|
北美洲 |
| |
亚洲 |
| |
欧洲 |
|
同理，可得到有关南半球的情况：
表 5-2南半球数据
区域 | 病毒亚型 | 时间 | |||||||
2009.04 | 2009.05 | 2009.06 | 2009.07 | ||||||
权值 | 百分比 | 权值 | 百分比 | 权值 | 百分比 | 权值 | 百分比 | ||
撒哈拉以南非洲 | H1 | 73.24 | 29% | 147.35 | 39% | 322.79 | 55% | 339.16 | 47% |
H3 | 42.78 | 17% | 68.29 | 18% | 136.80 | 23% | 185.59 | 25% | |
B | 132.60 | 53% | 158.22 | 42% | 124.49 | 21% | 204.58 | 28% | |
A | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | |
南美洲 | H1 | 402.36 | 40% | 1232.37 | 62% | 617.42 | 47% | 686.54 | 34% |
H3 | 19.76 | 2% | 19.76 | 1% | 0.00 | 0% | 0.00 | 0% | |
B | 318.37 | 32% | 438.31 | 22% | 586.49 | 45% | 896.06 | 45% | |
A | 258.60 | 26% | 312.35 | 16% | 107.98 | 8% | 410.48 | 21% | |
大洋洲 | H1 | 0.00 | 0% | 0.00 | 0% | 165.74 | 14% | 165.74 | 9% |
H3 | 0.00 | 0% | 200.00 | 50% | 583.68 | 48% | 937.04 | 51% | |
B | 165.74 | 100% | 200.00 | 50% | 468.52 | 38% | 732.53 | 40% | |
A | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | 0.00 | 0% | |
根据上述数据，我们可以得到南半球冬季二联装疫苗成分的预测：
南半球（2008.04-2008.07） | 撒哈拉以南非洲 |
|
南美洲 |
| |
大洋洲 |
|
参考
[1] 姜启源、谢金星、叶 俊，《数学模型》，北京：高等出版社，2003.8
[2] 苏金明、阮沈勇，《MATLAB实用教程》，北京：出版社，2008.2
[3] 欧春泉、邓卓辉、杨 琳、陈平雁，《用自回归模型预测流感样病例数的变化趋势》，《卫生统计》，第24卷第6期：569-571，2007.12
[4] 张善文、雷英杰、冯有前，《MATLAB在时间序列分析中的应用》，西安：西安电子科技大学，2007.4
[5] 张树京、齐立心，《时间序列分析简明教程》，北京：清华大学出版社，2003.9
[6] 小田切孝人，《流感病毒感染性疾病和相关疫苗的临床应用专辑》，www.cpvip.com, 2008年4月25日23：24
[7] 漆莉，《重庆市2004-2006年流感流行特征分析专辑》，www.cnki.net. 2008.4.26.11:23
[8] 朱大方，《江苏省流感症状监测方法研究》，www.cnki.net. 2008.4.27.1:03
[9] 刘大海、李宁、晁阳，《SPSS 15.0统计分析》，北京：清华大学出版社，2008.5
