新疆葡萄滴灌设计中采用布瑞斯勒（Bresler）公式确定滴头间距方法
摘要：滴灌工程设计中，滴头间距对于整个系统的效率、灌水质量来说是一个很重要的参数，而现有的资料和生产实践中，该值大多是根据实际情况进行估计的。本文介绍采用布瑞斯勒（Bresler）公式确定滴头间距的方法。
关键词：滴灌 滴头间距 土壤水势
1 引言
滴灌是当今世界最先进的灌水技术之一。在正确的系统设计和高水平的田间作物水分管理条件下，滴灌系统能够适时适量地进行灌溉，在作物的根区创造出适宜的水、肥、气、热条件，从而获得节水、高产、优质的效果。全国微灌面积约300万亩，其中大部分是“九五”期间起来的。我国进入WTO后，国外设备与国产设备价格差距正逐步缩小。新世纪我国进入全面建设小康社会，、农业结构都在进行调整，“2001年~2010年微灌发展战略”表明灌溉未来的发展趋势是精确灌溉和节约能量。机控制将是灌溉自动控制系统的一个组成部分，将气象、土壤、水分、作物资料等的数据输入计算机，计算机对这些数据进行处理分析，输出指令，电磁阀根据指令操作灌溉系统工作。这样，在滴灌系统设计中根据土壤资料和滴头流量确定滴头间距显得愈加重要。滴头间距过密，使湿润重叠区域加大，会加大不必要的工程投资；滴头间距过大，会使作物根系不能得到足够的水分，无法达到滴灌节水高产的效果。本文介绍在确定新疆伊宁葡萄滴灌设计中，采用的布瑞斯勒（Bresler）公式确定滴头间距方法。
2 计算方法
现将以色列滴灌专家布瑞斯勒（Bresler）教授确定滴头间距的程序介绍如下。
2.1 土壤的物理水力性质
根据所讨论的土壤类型，从不同类型土壤的典型物理水力参数（表1）中查出，砂壤土的饱和土壤渗透系数 
以及土壤特性常数 为：
表1 不同类型土壤的典型水力参数
土 壤 | -h（ |
|
|
粘 土 | 1.02~104 | 8.64×10-4 | 2.54×10-6（0.009 |
壤 土 | 1.3~890 | 7.26×10-3 | 1.44×10-5（0.05 |
砂壤土 | 43.3~300 | 1.69×10-2 | 3.9×10-4（ |
砂 土 | 58.4~147.2 | 0.466×10-2 | 1.27×10-2（45.7 |
2.2 计算饱和区土壤浸润最大半径 
根据布瑞斯勒（Bresler）提出的水份浸润土壤后期饱和区不同滴头流量最大半径公式（1），计算几种可能选择滴头不同流量 
时的最大半径：
（1）
式中： 
——浸润饱和区最远半径， 
——土壤特性系数， 
——滴头设计流量， 
——饱和土壤渗透系数， 
当 , 
当 
时， 
2.3 选择适宜土壤含水率上下限
根据采集的土样，用压力膜法，获得一组土壤水吸力与土壤含水率间的试验数据。以土壤水吸力为纵坐标，土壤含水率为横坐标，画出一条土壤水分特性曲线（图1）。选择适当的临界土壤含水量 
值，就可以从该曲线中获得相应的土壤水吸力值，此值的负值为非饱和土壤水的基质势，也就是相应的临界土壤水势 
值。
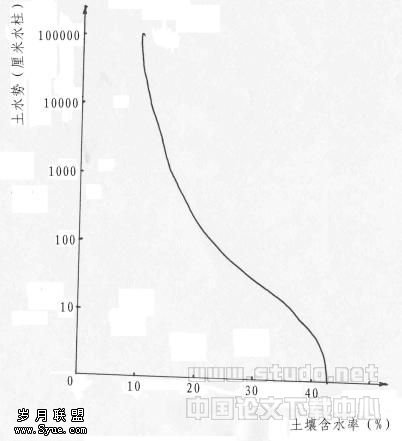
图1 砂壤土水分特性曲线
从图1中查得：田间持水量（占土壤体积百分比） 
时， 
；
适宜土壤含水率上限为田间持水量的90%， 
时， 
；适宜土壤含水率下限为田间持水量的60%， 
时， 
。
2.4 计算转换土壤水势函数 
的比值
根据公式（2）可以计算转换土壤水势函数临界值与饱和值的比值 ：
（2）
式中： 
——转换土壤水势函数，
——饱和土壤的转换土壤水势函数值，
——非饱和土壤临界土壤水势函数 时转换土壤水势函数值，
——临界土壤水势， 
，
——对数
当 
时， 
当 
时， 
当 
时， 
2.5 计算无因次土壤特性常数值α
应用土壤饱和区最大湿润半径 
，采用以下公式
（3）
计算无因次土壤特性常数 
值。式中 为无因次土壤特性常数值，其他同前。
当 
时， 
， 
当 时， ， 
2.6 查出相应的无因次半径 
值
定义非饱和区湿润径向半径与饱和区径向最大半径比值为无因次半径 ，
（4）
式中： ——无因次径向半径；
——非饱和区径向半径。
无因次半径 与 呈函数关系，根据不同的 值，绘出 —— 曲线，如图2所示，从图2中可以根据不同的 值和 值查出无因次半径 值。
当 时， ，
时， 
时， 
时， 
图2 无因次半径 值表
2.7 计算非饱和区湿润径向半径
从公式（4）中可推出， 
，可以计算非饱和区设计不同滴头流量的临界径向半径 值，滴头间距为：
（5）
式中： 
——滴头间距， 
；
采用公式（5），计算滴头间距如下：
时， 
时， 
时，
2.8 确定滴头间距
将应用土壤水力特性和不同滴头流量计算湿润区径向半径的结果列出，计算滴头间距如下表2。
表2 计算滴头间距列表
参数
量纲 选择 采用公式 | 流量
1 | 饱和区 半径
1 | 临界 水势
2 | 水势 比值
2 | 土壤常数值
4 | 无因次 半径
3 | 滴头 间距
5 |
1 | 2 | 5.63 | -10 | 0.844 | 0.048 | 1 | 11 |
-100 | 0.183 | 2.1 | 24 | ||||
-200 | 0.033 | 10 | 56 | ||||
2 | 4 | 10.60 | -10 | 0.844 | 0.09 | 1 | 21 |
-100 | 0.183 | 1.9 | 40 | ||||
-200 | 0.033 | 6.5 | 138 |
对于某一确定的土壤水势 
值，在滴头流量 与其间距 之间，均可选择最佳的组合。如表2中，滴头流量 的滴头，滴头间距 时，从地表滴头算起的土壤湿润体的径向湿润半径 ，在沿着毛管的方向，湿润区可以重叠，而 时的滴头的湿润范围过大，所以选择滴头流量 ，滴头间距 的滴头比较合理。
3 小结
传统的重力灌溉方法其主要的设计规范之一是在地表获得均匀的配水方案，而滴灌的配水方式是从每一个滴水源遵循土壤水力特性向土壤渗透的过程。这样，在滴灌设计中，为了提高滴灌系统的水分和养分的有效利用率，滴头间距 和滴头流量 必须与土壤的湿润特性和作物的灌水频率周期 及灌水时间相适应，而土壤湿润体的径向距离 和距离滴头的湿润体深度 的估算对设计和管理滴灌系统显得十分重要。
布瑞斯勒（Bresler）确定滴头间距的程序给我们提供了基本的准则：根据土壤的水力学特性资料 和 以及设计滴头流量 ，采用布瑞斯勒（Brasler）提出土壤饱和区浸润最大径向半径公式计算出 值，然后根据其相关的公式可以计算出不同滴头流量时的合理的滴头间距。
1 陈渠昌，吴忠渤等，滴灌条件下沙地土壤水分分布与运移，灌溉排水，1999,18（1）
2 朱德兰，李昭军等，滴灌条件下土壤水分分布特性研究，水土保持研究，2000，3，第7卷第一期
3 Joseph Shalhevet , Eshel Bresler and Xu Yuexian , Water Use and Efficiency in Agriculture, Institute of Soil and Water , Agricultural Research Organization , The Volcani center . Bet Dagan 50250 , Israel , 1992
4 S.Armoni Micro-Sprinkler Irrigation , Kibbutg Dan , Israel , 1986
5 Theory and Practice of Water-saving Agriculture, 中以两国双边节水农业国际学术研究会集，黄兴法，李光永，曾德超，RDI——The New Technique of Water Saving Irrigation Management in China, 水利出版社，2000
