和谐城市评价指标体系框架设计
内容摘要:我国城市和谐社会评价指标体系的构建是一个方兴未艾的课题,在城市建设实际层面和城市评价的学术研究层面都有亟待解决的需要。笔者充分考虑这一现实需求,着力于评价指标体系的构建,力求为致力于和谐社会评价的学习者提供基础的资料,同时也为建设和谐社会的操作者提供的样例。
关键词:城市 和谐社会 评价指标体系
评价指标体系的框架设计
(一)评价指标体系的建立方法
已有指标体系的建立方法大体可以归纳为四类:系统法、目标法、归类法、指标权重的确定方法。系统法就是先按研究对象和谐的系统学方向分类,然后逐类定出指标。目标法又叫分层法,首先确定研究对象和谐发展的目标,即目标层,然后在目标层下建立一个或数个较为具体的分目标,称为准则(或类目指标),准则层则由更为具体的指标(又叫项目指标)组成。在应用目标法时,研究者通常将系统的综合效益作为目标,把社会效益、效益、生态效益作为准则,选取有关要素作为评价系统是否具有和谐发展能力的指标因子。归类法就是先把众多指标进行分类,再从不同类别中抽取若干指标构建指标体系。指标权重的确定方法最初依据研究者的实践经验和主观判断来确定权重,但指标权重的准确与否在很大程度上影响综合评价的准确性和性。随着研究的深入,这种方法逐步发展为用特尔非法来确定权重。
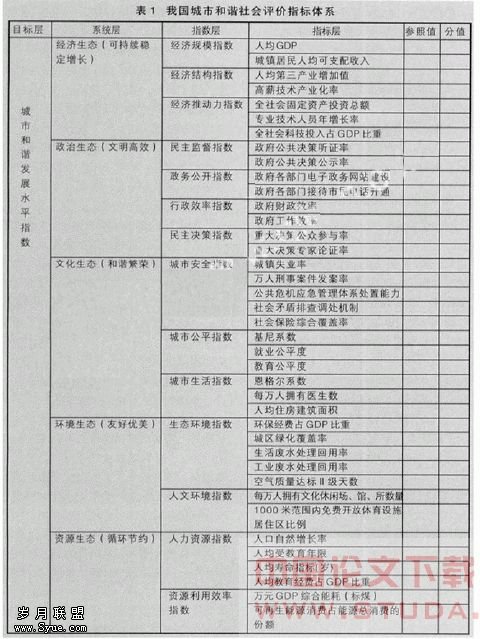
鉴于和谐城市评价体系的多子系统、多层次特点,这一体系的指标和权重可分两部分生成,即主成分分析法和德尔菲法结合使用。综合来看,从“和谐”的本质要求出发,可以考虑表1的框架设计。
(二)城市和谐社会评价体系层次
目标层——高级综合指标。为了从宏观上反映城市和谐社会的整体态势,可以按不同年限对城市的和谐发展进程进行纵向比较,也可以在一定程度上同其它城市做横向比较,可以设计一个高级综合指标——城市和谐发展水平指数。该指数是城市和谐社会系统总体运行效果、经济生态、社会生态、环境生态、资源生态之间相互协调程度,以及和谐社会的发展潜力与人为调控和谐能力的综合体现。
系统层——系统指标。为了进一步刻画城市和谐社会系统中经济、、文化、环境、资源对高级综合指标的作用和影响,可以设计经济生态、政治生态、文化生态、环境生态、资源生态 5个系统指标。这些指标是根据高级综合指标的发展特征与发展目标而设置的,是各子系统协调发展水平的集中表现。这些指标由若干指数指标具体描述。
指数层——子系统分项指标。各分项指标是描述城市和谐社会各系统具体项目的指标,划分的出发点是能够在各系统与各细分指标之间建立一个指标选取的方向,一是可以体现细分指标对子系统的代表性,二是有意识的把细分指标的各指标按照实际操作部门大致分类,以便提高指标体系的操作性,在以后的统计、规划等环节中可以有针对性的找到相关责任部门,也可以在确定各要素的权重时起到指引作用。
指标层——细分指标。为了给操作过程更多的指标选择性,在考虑要素关联的基础上,尽可能全面而典型地确定指标的个数,本研究构想提供了39个细分指标。
需要说明的是,在指标体系的框架中还包括参照值和分值两部分。参照值对于城市和谐度的评价能够起到大体测评作用,为实际评价部门提供政策的依据,这也是评价体系建立的深层次要求,即对于城市来说,各项指标在哪一个值上是大体和谐的。
评价方法的使用
(一)综合评价方法
评价是指根据确定的目的来测定对象系统的属性,并将这种属性变为客观定量的计值或者主观效用的行为。和谐城市评价是一个多指标多层次系统综合评价问题。综合评价则是指对以多属性体系结构描述的对象系统做出全局性、整体性的评价,即采用一定的方法,根据所给的条件给每个评价对象赋予评价值(又称评价指数),再据此择优排序,构成综合评价的基本要素有评价对象、评价的指标体系、评价专家及其偏好结构、评价模型等。用于综合评价的方法见表2所示。
多指标综合评价方法是把描述被评价事物多个不同方面且量纲不同的统计指标,转化成无量纲的相对评价值,并综合这些评价值以得到对该事物一个整体评价的方法系统。其中最重要的两个步骤是无量纲化和确定选取指标的权重。
无量纲化是将无法比较的不同量纲的指标实际值转化为无量纲的评价值。也采用许多数学变换来消除原始变量(指标)量纲的影响。无量纲化方法归纳起来主要有3类:直线型、折线型和曲线型。实践中通常采用直线型无量刚化方法。直线型无量刚化方法在将实际指标值转化成不受量刚影响的指标评价值时,假定两者之间呈线性关系,指标实际值的变化引起指标相应比例的变化。这种处理方法主要有阈值法(也称临界值)、Z-score法(中心化处理方法)、比重法等。其中,功效比重法操作起来较方便。
科学地确定指标权重在多指标综合评价中举足轻重,指标权重的确定方法也多种多样,大致可分为主观赋权法和客观赋权法。根据各指标间的相关关系或各项指标值的变异程度来确定权重数,避免人为因素的偏差,如主成分分析法、因子分析法等。
根据自身的研究条件,主成分分析方法可以被选择,因为就主观赋权法而言,主要是从评价者的角度认定各评价因素重要程度如何而确定权重数,依靠的是专家的修正环节。而客观赋权法中的主成分分析法是采用数学得出指标的重要程度、影响量,所以实用性很强。确定权重方法的使用前提是大量的统计数据已获取,对于有些城市的操作顺序(有些城市是数据整理与建立指标体系同步进行)是不可取的。而实际上各城市用于操作的指标评价体系多是集合专家的意见,用德尔菲法确定权重的,因为这种方法操作简便而且调整起来很灵活,尤其是一些描述性的指标,更容易按各自城市的特色赋予权重。
(二)评价模型的建立
应用数理方法及层次分析法(AHP),设计出既能反映城市特定时刻和谐水平,又能判断城市协调趋势,从而对城市和谐社会做出综合评价的集成评价模型。这里所谓的“集成”是指各种数学方法的综合应用。可以按如下步骤建立该评价模型:

和谐发展水平综合指数:和谐水平综合指数是和谐城市系统发展水平的集中体现。本研究依据该指标特征,运用递阶层次综合评价法来完成对它的,即:
各系统的和谐发展水平指数。根据以上所设计的评价指标体系框架,首先确定各细分指标的功效值(无量纲化的结果),然后根据权重进行加权处理得出各层指数,再次加权处理得到系统和谐指数。
细分指标的功效函数:设和谐城市评价指标体系的指标变量为uI(I=1,2,…,n),评价指标为XI(I=1,2,…,n),aI为系统稳定的均值、bI为系统和谐的参照值。和谐指标评价体系中各指标变量的功效值表示为:
UA(uI)=(XI-bI)÷(aI-bI),UA(uI)具有正功效时。
UA(uI)=(bI-XI)÷(bI-aI),UA(uI)具有负功效时。
说明:式中UA(uI)为指标对系统有用的功效,A为系统的稳定区域(I=1,2,…,n)
指数层指数函数:可用线性加权法对每一个指标功效配以权重系数wI(wI<1,∑wI=1),指数函数可表示为:
C=∑wIUA(uI)(其中I=1,2,…,n∑wI=1)
系统和谐度函数:可用线性加权法对每一个指数层指数配以权重系数yI(yI<1,∑yI=1)
D=∑yICI(其中I=1,2,…,n ∑yI=1)
城市和谐发展水平函数:可用线性加权法对每一个系统层指数配以权重系数zI(zI<1,∑zI=1)
E=∑zIDI(其中I=1,2,…,n∑zI=1)
和谐度介于0~1之间,大于0.8时城市处于高度和谐;在0.6和0.8之间为比较和谐;在0.5和0.6之间为基本和谐,小于0.5为不和谐,小于0.3 为极度不和谐。
诚然,城市是一个动态系统,其复杂性决定着不可能有完全一致的评价体系,每个城市都有特定的城市环境,也有特殊的生态要素,考虑城市自身的实际是构建评价体系的关键,在构建具体评价体系时量体裁衣是必须考虑的。本框架旨在提供方法的探讨和指标的初级选择。