关于时间数列回归与相关分析中的自相关问题

　　关键词:自相关　回归分析　时间数列　随机误差

　　论文摘要:本文针对动态时间数列与静态截面数据组成的数列之间在性质与结构方面的特点、差异,探讨了运用回归与相关分析理论对动态时间数列进行数据处理时出现的问题及解决的具体办法。

　　一、自相关的特征

　　回归与相关分析是统计学中的重要内容,其理论与方法已形成完整的体系,并在社会现象与科技领域得到广泛的应用。它既适用于研究宏观方面的问题,也适用于研究微观方面的问题。在早期,回归与相关分析主要用于厂家横向的截面数据中某些现象之间的相关程度和依存关系,近年来已被用于动态的时间序列分析上,特别是在经济分析、经济预测等方面的应用,很受人们的重视,回归与相关分析方法的应用范围进一步扩大了。但值得注意的问题是,在反映动态的时间数列与反映静态的截面数据组成的数列之间,在性质与结构方面存在一些不同的特点,因而在研究方法上也具有一些特殊性。提出本文的目的之一也在于就其中一些问题做一些探讨。

　　对时间数列进行回归和相关分析,首先遇到的问题是大量的时间数列中存在着受某些因素影响形成的长期趋势,因而在数列前后期的水平之间存在着一定程度的依存关系。例如:某一地区的人口数的变动就受该地区前一时期人口数多少的影响,一个地区社会商品零售额的增长,也受到该地区前期水平多少的影响等。这种按时间先后顺序排列的同一个变量前后期水平之间存在的相关关系,统计中称之为自相关或序列相关。自相关主要是在时间序列分析中提出的概念,在截面数据形成的序列中很少出现。但在研究时间序列时,也因研究目的和数列自身性质的不同而采取不同的步骤和方法。当研究的是由一个变量组成的单一时间数列,研究目的是为了分析其自身的变化而不涉及与其它变量的关系,特别是当某一现象的变化难于与其它原因建立联系时,这就需要从变量自身的变化中提取有关未来的信息。例如关于地震、太阳黑子变动等现象的观测或预报,这就需要用到自回归和自相关,而且在最后对所采用的回归模型是否有还要经过检验,如果误差项存在自相关,也要设法予以消除。另一种情况是研究的对象不是单一的时间数列,而是由双变量或多变量组成的相关时间数列(或以时间t作为解释变量组成的数列)。在这种情况下,要确定的不是单一数列自身的增长趋势,而是和在截面数据中进行回归分析相似,目的是确定解释变量变动与因变量变动之间的依存关系。这时要用到各项回归与相关分析的理论和方法,但不同的是这里的数列是动态的,存在自相关,问题因此变得复杂起来,由此而产生了在时间数列中应用回归分析方法的特殊性,本文着重讨论的将是这方面的问题。

　　时间数列水平之间存在自相关,将会产生什么样的后果呢?首先是回归模型中误差项必须遵守的基本要求和条件受到破坏,特别是相互独立性受到了破坏,其结果是现象之间存在的真实关系可能被歪曲或被掩盖起来。相关数列中的波动,取决于数列自身的趋势,即受数列内部存在的自相关的制约。在这种情况下,通常的各种显著性检验(F检验、T检验)也将失效,预测分析也都失去意义。为了避免出现上述结果,并能满足回归分析的基本要求,就需要对相关数列是否存在自相关进行检验,并且如果被发现,就用方法予以消除,以求通过回归得出正确的结论。

　　二、自相关的形式

　　时间数列是否存在自相关,可以从数列的前后期水平之间反映出来,但在回归分析中,主要是通过回归模型中的随机误差项μt来进行的。随机误差也形成一个数列,其中包含着大量的未被利用的信息。下面以最常见的一阶自回归为例,从误差项着手,对数列是否存在自相关进行检验,确定它的强弱程度以及消除的方法。设Y对X的回归模型Yt=β0+β1xt+μt(1)式中,μt满足除没有自相关而外的关于线性回归模型的一切条件,若μt存在自相关且仅与前一期μt-1有关,即μt=f (μt-1),则称μ具有一阶自回归形式。如果μt与μt-1的关系是线性的,即μt=pμt-1+vt(2)则称μ具有一阶线性自回归。

(2)式中,ρ为自回归系数或自相关系数,

公式为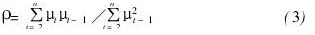

式(3)一方面显示μt与μt-1的相关程度(0<p≤1是正自相关的,-1≤p≤0是负自相关);另一方面显示vt满足线性回归模型的所有假设条件。如果μt的取值不仅与μt-1有关,而且与前几期的取值也有关,即μt=f (μt-1,μt-2,…,μt-m),则称为高阶自回归。

在式(2)中,自相关系数ρ是个很重要的指标,它反映自相关是否存在以及它的强弱程度,但在研究实际问题时,ρ通常是未知的,μ也是未知的,只有通过样本值来估计它们。当我们获得样本数据用最小平方法求出模型(1)中的系数β0,β1,便可计算回归残差et=Yt-^Yt=Yt-(^β0+^β1xt)我们将用et估计μt,于是式(3)的样本相关系数可以写成

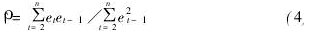
在大样本条件下, ^ρ可以作为ρ的无偏估计量。

　　三、自相关的检验

　　检验误差项是否存在自相关的方法主要有图示检验法、回归检验法、冯·纽曼比率(VonNeumann’s ratio)检验和德宾·沃森检验(Durbin Watson test)。其中最常用的是德宾·沃森检验,也简称D·W检验。它适用于误差项具有一阶自回归的自相关。D·W检验统计量d的计算式为:

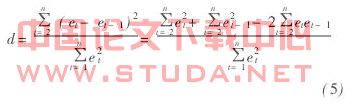
由于统计量d是根据回归残差et计算的,而et在回归分析中是要经常计算和应用的,所以, D·W检验获得了普遍的使用。

当给定样本容量n、解释变量个数K及选定的显著性水平α,可查D·W检验上下界表,找出临界值dL. dμ。具体情况由d分布的临界域图形做出比较判断。

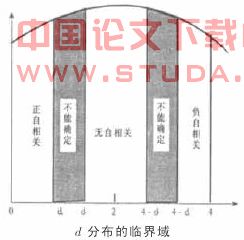
　　从图中可看出,若d<dL,即d落在图的左区,μt为正自相关;d>4-dL,即d落在图的右区,μt为负自相关; dμ<d<4-dμ,即d落在图的中间区域,μ1不存在自相关;dL≤d≤dμ或4-dμ≤d≤4-dL,即d落在无结论区域,检验不能做出结论。D·W检验存在无结论区域,这是一个欠缺。当实际出现这种情况时,解决办法就是适当增大样本容量,在多数情况下都能检验出误差项有无自相关。

　　经D·W检验结果,若是证实误差项存在自相关,则应首先查找产生自相关的原因,这时要从所选的解释变量以及回归模型数学形式是否适合等方面进行审查,如有不适则应进行调整修正,并重新进行检验。当这些因素被排除之后确认属于数列自身存在自相关,则需进一步研究如何消除自相关的方法。

　　消除自相关的办法之一就是变换原始数据,形成新的模型,使误差项能满足普通最小平方法的假设条件,以获得有关参数的最优无偏估计。由于自相关的结构形式不同,对原始数据的变换方式也不同,因而产生不同的方法,一般总称为广义最小平方法。

　　1·差分法

仍用前例,设Y对x的回归模型为

Yt=β1+β1xt+μt(7)

μt=ρμt-1+vt

式中, vt满足最小平方法关于误差项的全部假设条件。

将式(7)滞后一个时期,则有

Yt-1=β0+β1xt-1+μt-1(8)μt-1=ρμt-2+vt-1

于是, (7)-ρ×(8),得Yt-ρYt-1=β0(1-ρ)+β1(xt-ρxt-1)+νt(9)

Yt-ρYt-1=β1(xt-xt-1)+μt-μt-1=β1(xt-xt-1)+vt(10)

也就是说,一阶差分法是广义差分法的特殊形式。

　　2·自相关系数ρ的估计方法

　　差分法是在自相关系数ρ已知的前提下, 通过变换数据消除了自相关性;但通常ρ多是未知的,而且与1又有一定的差距,因此在多数情况下需要对ρ的数值进行估计,而后再通过数据变换消去之。常用的估计方法是:

(1)由统计量d估计ρ。从D·W检验中已知: d≈2(1-ρ),因而有

　　需要注意的是,使用式(11)估计ρ值,要在大样本条件下才能渐进地有效。(2)迭代法。这种方法是通过反复迭代才逐步逼近ρ的真实值的方法。下面仍然以一元回归模型(7)为例来说明。

　　首先,对与式(7)相对应的样本回归模型应用最小平方法求出回归系数β0、β1的第一次估计量^Yt(=^β0+^β1xt)和μt的“第一轮”估计值et(=Yi-^β0-^β1xt),根据所得et,用前面已给出的公式(3)得出ρ的“第一次”近似值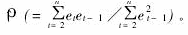

　　其次,做差分模型 ,对差分模型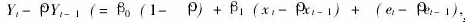应用最小平方法求得参数^β0、^β1的第一次(即β0、β1的第二次)估计值^^β0、^^β1,并“第二轮”的误差估计量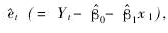且依据^et计算ρ的第二次估计值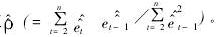

模型应用最小平方法求得参数^β0、^β1的第一次(即β0、β1的第二次)估计值^^β0、^^β1,并计算“第二轮”的误差估计量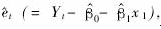且依据^et计算ρ的第二次估计值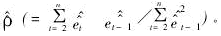

最后,重复进行这一迭代过程,求出第三次,直至第s次,估计值收敛为止。

　　柯奇兰——奥卡特(D. Cochrane——G.H. orcutt)两步法便是在求得“第二轮”估计量^^β0、^^β1后就达到了目标而停止迭代过程。另一种可以采用的控制迭代的方法是:在假设误差项存在一阶自回归形式的自相关时,对于每一步迭代均用D·W检验法进行检验,计算d统计量,直到通过零自相关检验则停止迭代。对于存在高阶自相关(比如有二阶或三阶自相关)形式的误差项,求ρ的估计值就比较复杂,但是其步骤与一阶自回归的运算过程相同。