AHP法在确定区域生态经济评价指标权重的应用探讨
摘要 层次分析法是一种定性分析与定量分析相结合的多目标决策分析方法。对于区域生态的评价而言,建立的评价指标体系是非常复杂的过程,它涉及到很多指标。文章阐述并运用层次分析法,为确定区域生态经济评价指标的权重提供了可行的途径,能较好地避免评价过程中的主观随意性。
关键词 生态经济 层次分析法 权重 应用
建立科学的评价指标体系,是对区域生态经济进行有效评价和提高评价结果信度与效度的关键。要准确评价区域生态经济现状,必须确定各指标的权重,因为指标权重的合理与否在很大程度上影响综合评价的正确性与科学性。AHP法为准确确定区域生态经济评价指标间的权重提供了可行的途径。[1]
一、层次分析的基本原理[2,3,4]
AHP法是美国著名运筹学家萨蒂教授于20世纪70年代提出的一种定性与定量分析相结合的多目标决策分析方法。该方法自1982年被介绍到我国以来,以其定性与定量相结合地处理各种决策因素的特点,以及其系统灵活简洁的优点,迅速地在我国社会经济各个领域内,如能源系统分析、城市规划、经济管理、科研评价等,得到了广泛的重视和应用。
(一)AHP法的基本思想
它将问题条理化、层次化,构造出一个有层次的结构模型。在这个模型下,根据问题的性质和要达到的总目标,将问题分解成不同的组成因素,按照因素间的相互关系及隶属关系,按目标层、准则层和指标层依次排列起来,形成一个多层分析结构模型。在目标层以下各层,分别通过"两两比较"的方式确定层次中各因素的相对重要性,并最终判断最低层(方案、措施、指标等)相对于最高层(总目标)相对重要程度的权值或相对优劣次序的问题。
(二)AHP法的基本假定
它假定层次之间存在递进关系,即从高→低或从低→高递进。上一层次的因素作为准则对下一层次有关因素起着支配作用。
二、应用
(一)建立系统的递阶层次结构模型
对问题分解的不同组成因素分类,构造出一个各因素之间相互联结且有层次的结构模型。模型中[5],处于最高层次是分析问题的预定目标或理想结果,只有一个元素;中间层包含了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需考虑的准则、子准则,因此也称为准则层;最底层包括了为实现目标可供选择的各种措施、决策方案或指标等,因此也称为措施层、方案层或指标层。
区域生态经济评价指标体系分三层[1,6]:第一层为区域发展度X,第二层包括发展水平R1、发展效率R2、发展潜力R3、发展开放度R4、发展调控度R5、发展协调度R6,共六项,每项下面又包含若干个指标项。其分解示意图见图1。
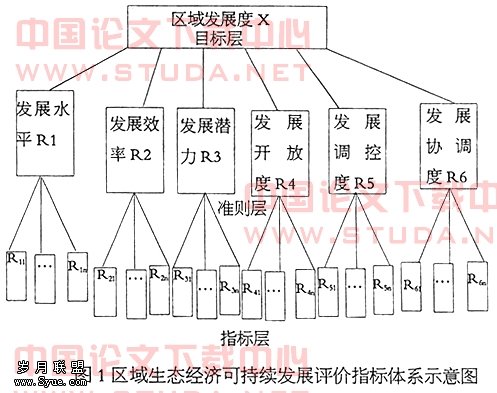
Figure 1 The Evaluation Index Systems of Eco-economic Sustainable Development
(二)构造出各层次中的所有判断矩阵
判断矩阵是运用AHP法的关键所在,是定性过渡到定量的重要环节,在通过求解判断矩阵的特征向量,并对判断矩阵的一致性进行检验,检查决策者在构造判断矩阵时判断思维是否具有一致性。由于判断两个指标间重要程度因人而异,为避免因个人因素对此产生太大的偏差,我们请多位专家学者分别作出判断,经综合确定各指标间的两两比较后的判断值,建立判断矩阵。
指标层次结构建立后,上下层指标间的隶属关系就被确定了,对同一层次指标进行两两比较,其比较结果以T.L.Saaty的1~9标度法表示。下表给出了1~9标度的含义。

(三)层次单排序及一致性检验
判断矩阵对应于最大特征值的特征向量,经归一化后即为同一层次相应指标对于上一层次某指标相对重要性的排序权值,这一过程称为层次单排序。
上述构造成对比较判断矩阵的办法虽能减少其它指标的干扰,较客观地反映出一对因子影响力的差别。但综合全部比较结果时,其中难免包含一定程度的非一致性。因此,对得出的判断矩阵有必要作一次一致性检验,以决定是否能接受它。
(四)层次总排序及一致性检验
上面我们得到的是一组指标对其上一层中某指标的权重向量。我们最终要得到各指标,特别是最低层中各指标相对于目标而言的排序权重,从而进行决策。总排序权重要从高→低将单准则下的权重进行逐层合成。
对层次总排序也需作一致性检验,检验仍像层次单排序那样由高层到低层逐层进行。这是因为虽然各层次均已经过层次单排序的一致性检验,各成对比较判断矩阵都已具有较为满意的一致性。但当综合考察时,各层次的非一致性仍有可能积累起来,引起最终分析结果较严重的非一致性。
三、结论与评价
区域生态评价指标体系是一个具有多层次、多指标的复合体系,在这个体系中,各层次、各指标的相对重要性各不相同,难以确定,常用的调查访问法、专家咨询法等方法很难达到理想效果。AHP法通过构造判断矩阵,先对单层指标进行权重,然后再进行层次间的指标总排序,来确定所有指标相对于目标的相对权重。利用AHP法,不仅可以降低工作难度,提高指标权重的精确度和科学性,而且通过采取对判断矩阵进行一致性检验,判断专家意见的一致性,有效地将定性分析与定量分析结合在一起,从数学分析的角度上给出了各个指标比较的数量关系[5]。
在应用AHP法过程中还应注意某些事项[7,8]。首先递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关,一般地层次数不受限制。每一层次中各元素所支配的元素一般不要超过9个。这是因为支配的元素过多会给两两比较判断带来困难。其次如果所选的要素不合理,其含义混淆不清,或要素间的关系不正确,都会降低AHP法的结果质量,甚至导致AHP法决策失败。为保证递阶层次结构的合理性,需把握以下原则:
1、分解简化问题时把握主要因素,不漏不多;
2、注意相比较因素之间的强度关系,相差太悬殊的要素不能在同一层次比较。
再就是层次结构反映了因素之间的关系,但准则层中的各准则在目标衡量中所占的比重并不一定相同,在决策者的心目中,它们各占有一定的比例。在确定影响某因素的诸因子在该因素中所占的比重时,遇到的主要困难是这些比重常常不易定量化。此外,当影响某因素的因子较多时,直接考虑各因子对该因素有多大程度的影响时,常常会因考虑不周全、顾此失彼而使决策者提出与他实际认为的重要性程度不相一致的数据,甚至有可能提出一组隐含矛盾的数据。这是构造两两比较判断矩阵时应注意的。
[1] 曹利军.可持续评价理论与方法.-北京:科学出版社,1999,118~182
[2] 王毅成,林根祥主编.市场预测与决策[M].-武汉:武汉大学出版社,1998.12
[3] 冯忠铨主编.经济预测与决策[M].-北京:财政经济出版社,1995.10
[4] 陈昌军,王紫雯.用层次分析法综合评价建设项目的环境影响[J].环境科学与技术,2006,29(8):108~110
[5] 彭国甫,李树丞,盛明科.应用层次分析法确定政府绩效评价指标权重研究[J].中国软科学,2004, (6):136~139
[6] 曹利军,周大杰,席玉英.区域可持续发展综合模型框架研究[J].数量经济技术经济研究,2000, (4):64~67
[7] 陈修兰.层次分析法应用于经济决策中的实例分析[J].山西煤炭管理干部学院学报,2006,(1):13~15
[8] 李霞,张本梁.层次分析法在房地产投资系统风险评价中的应用[J].工程建设与设计,2006,(1):65~66











