生产性公共开支经济中政府债务的福利损失
关键词：巴罗—李嘉图等价，借贷限制，生产性公共开支
一、引言
国债问题始终是经济学领域的一个重要问题。围绕着李嘉图等价定理能否成立这一问题，经济学者对最优国债进行了热烈的讨论，Barro(1974)对这一定理进一步完善和，提出了著名的巴罗—李嘉图等价。如果李嘉图等价定理成立，则政府发行公债和征税其实是没有差别。考虑到比例税将造成税收超额负担，Chamley(1981，1986)、Lucas(1990)和Turnovsky(1996)的文章中得到的结论是在比例税情形下，最优的资本收入税为零，政府成为净债权人。
与此同时，一些学者则认为李嘉图等价在现实经济中并不成立。比如经济中不存在着无限生命的个体、经济个体不具有理性预期，但这些论调从经济理论研究而言则过于草率和武断。但是，当消费者异质性、市场不完备等经济假设在经济理论中得到充分关注时，李嘉图等价定理不成立的论调也多起来。具有代表性的文章为Woodfood(1990)和Aiyagari(1994)，后者在消费者异质性和市场存在着借贷约束下，提出公债具有自我保险的作用，能够放松借贷限制。而在其后，Aiyagari(1995)更进一步提出了Chamley的结论并不成立，最优资本税不为零。此后，Aiyagari和McGrattan(1998)则把宏观经济模型数量化，通过美国经济的数值模拟，提出美国的最优债务存量水平为2/3，这一数目刚好为美国战后的平均水平。他们还认为当样本经济债务存量偏离最优债务存量水平时，福利损失非常小，不会超过千分之一。Floden(2001)在他们的基础上，进一步考虑转移支付的作用，结果与他们的结论基本保持一致，只是Floden发现转移支付的福利作用比公债大。
但是这些文章都有一个共同的不足之处：没有考虑政府对生产的影响。而政府对生产的影响无论在理论研究还是在实证研究方面都得到了一定的认可。在已有的研究中，一种考虑的是存量形式即公共资本参与生产，而另一种形式则是流量形式即公共开支参与生产。本文采用的后一种形式，即Barro(1990)中所提出的生产函数形式，考虑到现实经济中有一部分政府公共开支对生产没有直接影响，我们在文章中将公共开支分为消费性公共开支和生产性公共开支，后一种公共开支才对生产有直接影响。由于在经济中，增长效应(growth effect)都比较大，因此，如果考虑了内生经济，则福利变化可能将很大，我们也将在文章中检验这一经济直观成立与否。
尽管中国的公债可以追溯到封建社会，但是从我们研究的对象而言，则集中在新中国成立以来的债务情况。新中国从50年代就开始发行国内公债，先是“人民胜利折实公债”后是“国家经济建设公债”，此外还有向前苏联举借的外债。中国的理论界对这些公债的作用都持较为肯定的态度，不过从80年代恢复发行公债以来，大家对公债的看法就出现了褒贬不一，公债也因此成为财政领域一个热门话题。1998年实行的积极财政政策和此后实行的双稳健政策，公债发行数量大幅度地增加，这引起了许多经济学者的极大关注，理论界关于债务发行数量是否合理从几个债务指标展开了激烈的讨论。如贾康和赵全厚(2000)从理论上认为国债规模与国债效应存在一个倒U型关系，这导致了最优债务规模的存在。另一方面，他们从中国经济统计中的实证数据得到国债的债务指标，对比国际上这些债务指标经验值得出中国国债依存度严重超标而国债负担率又远未超标这一悖论进行解释。他们持有的观点是现实的国债规模被低估，因为忽略了国家的或有负债。周佰成等人(2002)则从国债的偿债率、依存度和累积负担率3个指标出发，以国际上这些指标的经验值作为基准，建立国债发行的最优规模。刘溶沧和马拴友(2001)从中国的实证数据出发，考虑了赤字、国债与经济增长的关系。这些文章尽管做出了一定的学术贡献，但是，他们在讨论时，只局限于参照国际的一些经验标准或从短期的一些计量指标展开，而并没有从长期一般均衡和经济模型数量化的角度来考虑这个问题，另外，他们对国债的考虑，并没有从直观上给出国债造成福利损失有多大。林细细和龚六堂(2007)在Aiyagari和McGrattan(1998)文章的基础上，结合中国经济现状，对中国国债政策进行福利分析。结果发现在中国目前的样本经济状态(1978-1998)下，较大量发行公债并未带来很大的福利损失，尽管这损失数额比Aiyagari和McGrattan(1998)的结论来得大。但该文章没有考虑政府公共开支对生产的影响。
本文在林细细和龚六堂(2007)的基础上，结合中国实际，考虑了生产性公共开支的内生经济中最优的债务规模及福利影响。由于模型是建立在封闭经济下，因此我们考虑的债务为国内公债，即不包含外债。我们发现，由于政府公债的正效应在中国目前的情形下较小，从而不足以抵消其负的效应，因此，最优的公债水平将为负。但是，我们发现，目前较大规模地发行政府公债，其福利损失将非常大。相对于中国样本经济，债务存量每提高10%，将产生2%左右的福利损失。这一结论与林细细和龚六堂(2007)差别很大，公债问题需要引起足够重视。
本文以下结构安排，第二部分为模型部分，我们建立基本模型并讨论政府公债的作用。第三部分我们对模型进行参数化并说明模型方法。第四部分为数值模拟部分，我们得出数值模拟结果并讨论结果的敏感性(Robust)。第五部分为政策分析部分，我们分析现行公债政策带来的福利影响。最后我们得出本文的结论并指出文章的一些不足之处。
二、模型
具有无限生命的经济个体，为了分析的方便，我们将其数量标准化为连续统1。每个人提供一单位劳动，但其劳动生产力et则存在着外在的冲击。每个人当期的et独立同分布，每个et在时间上遵循马尔可夫过程。为了简化分析，我们将平均的劳动生产力标准化，即E(et)=1。每期劳动者的劳动生产力加总后为固定常数，不随着时间的变化而发生变化，这样就不存在加总的不确定性。经济中不存在保险市场(或者说保险市场效率低下)，不过每个人可以交换两种无风险资产，即资本和政府公债。但是，在要素市场上，则是完全竞争。于是，当经济处于稳定增长时，在平衡增长路径上，尽管由于劳动生产力的冲击使得个人的消费、收入和财富将存在着波动，但是，人均收入、消费和财富将不变，且存在着一个稳定的分布。
与Aiyagari和McGrattan不同的是，我们考虑了现实经济中政府公共开支对生产的重要作用，在生产中改变了生产函数，采用Barro(1990)的生产函数形式，即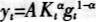
，其中yt、Kt、gt分别为人均产出、人均资本存量和人均政府公共开支。这种生产性的政府公共开支为纯公共产品，政府仅仅发生支出，无从体现其报酬。当要素市场和产品市场为完全竞争时，我们得到：
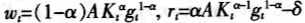
其中wt和rt分别为t期的工资和资本回报率，δ为资本折旧率。
消费者有两种收入来源，即资产收入和劳动收入。这些收入缴纳完税收，用于消费后剩余的资产留到下期。此外，消费者则面临着借贷约束限制，即其每期资产不能为负。消费者的即期效用函数为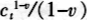
，其中υ为风险回避系数，ct为消费者在t期的消费。消费者最大化其一生的效用，其面临的问题可以描述如下：
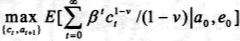
约束条件为
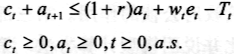
其中，αt为消费者在t期拥有的资产，Tt为消费者获得收益后缴纳的定额税收，β为效用的主观贴现因子。
我们认为政府是个仁慈的政府，他没有任何私人目的，且具有承诺能力(commitment)，政府的目标和消费者的目标一致：最大化消费者的一生总效用。政府可以通过发行公债和收税来取得收入，但是需要偿还到期的债务本息和发生一些政府公共开支，这些公共开支对生产具有一定的作用(体现在生产函数上)。于是，政府的预算约束方程为：
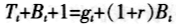
其中，Bt为政府在t期发行的非状态偶发性公债。
当市场达到均衡时，At=Bt+Kt。其中，At为经济中消费者拥有的资产总和。
为了较好地描述最优的债务规模，首先需要找一个指标来刻画。我们采用相对数指标，即政府公债占总产出的比重。与Aiyagari和McGrattan不同的是，我们在内生经济的模型框架下引入公共开支，为了较好说明经济状况，我们建立下面的引理。
引理1：在上述经济中，消费者进行最优化选择后，总消费、总资产、工资、总政府公共开支、税收、政府公债等人均总量指标占总产出的比重保持不变时，经济在平衡增长路径上。
这条引理的证明比较容易。根据平衡增长路径定义，各个总量指标沿着固定的增长率增长，只要令它们的增长率均为经济增长率，我们的引理得到证明。
通过引理1，我们将上述最优化问题进行转化为相对数指标。记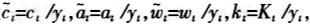
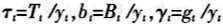。当经济处于稳定增长时，
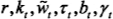均为固定常数，我们省略其时间下标。此时的经济增长率用ф表示，于是
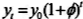。从生产者行为得到，
。
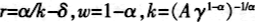政府的预算约束变为：
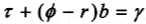(1)
记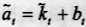
，消费者的优化问题
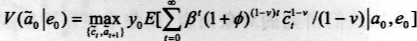
受约束于：
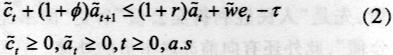
建立函数方程的Lagrange方程：
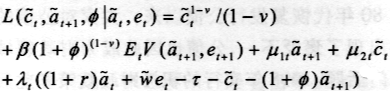
这样得到一阶条件：
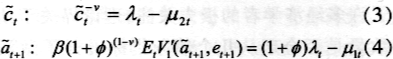
和松弛条件：
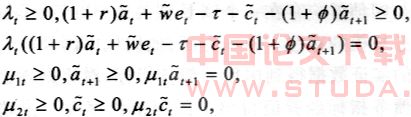
另外，由包络引理得到：
由方程(3)、(4)和(5)得到：
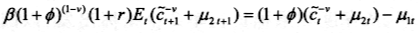
即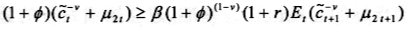
不等号在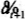
=0时成立，即借贷限制起作用时。上式简化为：
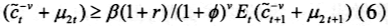
通过求解上述优化问题，我们将得到资产的决策规则，即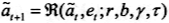
时，将该决策规则同劳动生产力冲击形成的马尔可夫过程，我们就可以用来计算关于资产和劳动生产力冲击的稳定联合分布，我们将这分布函数记为
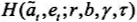。在得到稳定的静态分布基础上，我们将可以得到此时的人均资产，即
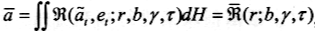，这人均资产表明了稳定状态下社会对资产的供给。而稳定状态下社会对资产的需求包括两个部分，即政府公债和生产所需资本。从而有
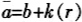。在政府税收、公债和生产性公共开支给定的条件下，我们将得到均衡的资本存量、利率和经济增长率。
如果一个经济满足下列条件，我们称为市场均衡：(1)存在一个稳定分布；(2)要素市场出清，即生产所需的资本和劳动恰好为市场的供给量；(3)消费者最优化条件得到满足；(4)政府预算平衡。
让我们转向政府。如果政府追求的目标是在固定生产性公共开支占总产出的比率(9的基础上合理选择政府债务水平。于是，我们从要素市场的均衡条件可以得到固定的利率水平和资本产出比率。我们继续考虑(6)式，当劳动生产力波动较大时，借贷限制在每期起作用。这样，当经济处于稳定增长时，在稳定分布中，将有一个正的测度满足借贷限制。将(6)式两边按照稳定分布取期望，得到：
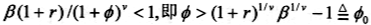
从这个式子我们得到一个有趣的结论，即在劳动生产能力存在异质性的情况下，借贷限制约束加剧了经济增长。借贷约束越强，经济增长越快，反之，则经济增长速度越慢。为最低的经济增长率，即借贷约束不起作用时的经济增长率。结合要素市场均衡利率方程，我们得到：
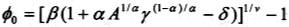
于是我们得到最低经济增长率与生产性公共开支比率的变化关系：
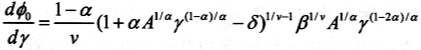
因为主观贴现因子小于1，生产函数中资本份额为小于1的常数，而折旧率也是小于1的常数，风险回避系数为正数，因此，我们得到最低经济增长率与生产性公共开支呈正相关关系。这样，为了保证有正的最低经济增长率，生产性公共开支水平不能太低，即不能低于
。
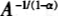下面，我们来考虑公债的作用。将政府预算约束方程(1)和
代入(2)式，我们得到新的约束方程：
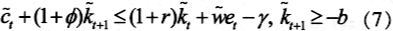
我们用(7)式代替(2)式，求解稳定分布下的消费者最优化问题。根据偏好的局部非饱和性原理，(7)式的第一个不等式在没有借贷约束情况下必然成立。但是，在存在借贷约束的情况下，如果劳动生产力波动太大，导致最低的劳动生产力所创造的收入足够小，为了满足消费额必须非负这个约束条件，在低劳动生产力的情况下，借贷约束起作用，即Kt+1=-b。因此，增加发行政府公债实际上起到放松借贷约束条件这一作用。在其他情况不变下，发行公债越多，用以缓冲劳动生产能力波动带来的收入冲击的能力将越大，这也就意味着消费将更加平滑，因此福利将得到改善。从另外一个角度看，借贷约束放松，消费者的收入波动将越小，而这种波动将转嫁到资本市场上，使得资本市场波动更大。这种大波动使经济处于较动荡状态，从而影响到经济的长期增长。即体现了Ramey和Ramey(1995)所得到的结论，波动与经济增长率成反比。这从消费者预算约束的欧拉公式更好理解。由于借贷约束限制越少，也将意味着消费者最优化的欧拉公式中更容易取等号，亦即经济增长率越趋向最近经济增长率。于是经济增长率下降，在其他条件不变的情况下，这将造成福利的下降。图1让我们更为直观了解债务存量变化对于经济增长率造成的影响。在图2中，当b从0.5提高到3时，资本供给曲线向右移动，这使得均衡时经济增长率下降。
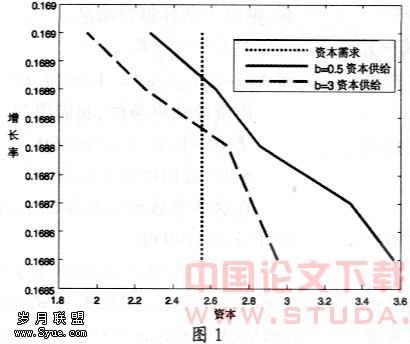
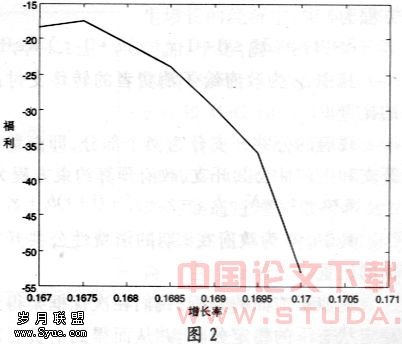
债务存量提高尽管将造成经济增长率下降，从而导致社会福利损失。不过我们从消费者的新预算方程(7)式发现，由于经济增长率的提高，将使得补偿经济增长的资本减少，这使得消费者留有更多的消费，这将提高消费的福利。图2为给定债务存量下，经济增长率发生变化导致的福利变化。我们也发现，一味地提高经济增长率并不一定会增加社会福利。经济增长率与社会福利形成倒U型的曲线。
因此，政府公债的发行从其正外部效应而言，可以提高消费率，改善社会福利。但是，政府公债的发行也存在着一定的负外部效应。首先，由于发行公债提高资产流动性，这降低了增长率。其次，从平衡预算的角度而言，发现公债需要用税收来补偿，如果用总额税形式，则将对所有消费者收取同样数量的税收，这将加剧低收入者的负担，加剧他们收入的不稳定。此外，如果采用比例税形式时，则还将造成税收的超额负担。
正因为这些正负效应之间的权衡为最优债务存量的确定提供了一个存在的合理理由。作为福利标准，我们采用功利主义的观点，从经济稳定状态出发，利用次优框架(Second-best)，考虑政府为了使得消费者福利最大化时，应如何选择公债水平和税收政策。即最大化目标函数
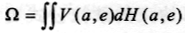
为了有效衡量最优债务存量带来的福利收益，我们采用卢卡斯(Lucas，1990)的方法，即在其他条件不变的情况下，考虑消费者达到样本经济时，其增加的消费水平占消费者目前消费水平的比重，如果为正，即为消费者没有达到最优债务水平时的福利损失，反之即为福利收益。
为了更好地对经济现状经济模拟，我们在第三部分将对模型进行拓展，并在拓展的基础上对经济参数进行赋值。
三、参数化及方法
(一)参数取值
为了更好地模拟现实经济，我们将模型进一步拓展。在政府税收方面，我们用比例税代替第二部分的模型里面的总额税，政府对资产和劳动同时征税，τw为工资税税率，λα为资产税税率。而劳动供给具有一定的弹性，消费者可以选择劳动的时间，但是消费者面临着时间约束。为了方便起见，我们将消费者的总时间标准化为1，lt表示为消费者在t期选择的休闲数量。消费者的效用函数为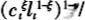
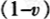，若为效用中的消费份额。消费者的预算约束方程为
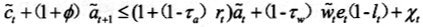
其中，χt为政府给予消费者的转移支付占产出的比重。
政府的公共开支分为两个部分，即消费性公共开支和生产性公共开支，政府预算约束方程为
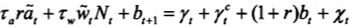
其中，
为政府在t期的消费性公共开支占产出的比重。
类似于前面的分析，我们在次优框架得到经济稳定状态下的稳定分布，并从而得到消费者对资产的供给和劳动的供给。然后根据市场均衡条件得到此时的经济增长率和劳动供给量，进而得到给定财政政策下的社会福利值
。
在此基础上，我们按照的一些实际情况对设定模型中的参数进行校正。我们考虑的样本经济为1978-1998年这20年中国的宏观经济指标。资本产出率、资本折旧率、人均实际经济增长率、国债余额、人均实效劳动时间，这几个数据我们采用林细细和龚六堂(2007)的数值，分别为3.4、0.0665、0.07、0.0432和0.24。劳动生产力的马尔可夫过程为
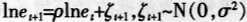
我们采用林细细和龚六堂(2007)取值，ρ=0.8和σ=0.06。
我们采用Barro(1990)的生产函数，关于生产函数参数的估计，我们采用反推的方法。在我们中国生产函数估计方面，尽管存在一定的争议，但是工资份额所占比重较低，这是一个不可否认的现实，于是，我们采用工资份额为0.4，这也就意味着α=0.6，这个数值和张军及邹至庄等人的结果基本保持一致。政府生产性公共开支γ我们采用0.06，而消费性公共开支(将具有生产性的公共开支和转移支出排除在外)γc我们采用0.0853，政府转移支出χ采用0.022。这3个政府决策变量的数据来源于《中国统计年鉴2001》和《中国统计年鉴2005》中1978-1998年中国政府支出和政府税收资料进行相应的平均。风险回避系数方面，我们试验性采用υ=1.5。
在此基础上，我们通过数值模拟得到其他参数值。首先，由下列两式得到样本经济的利率和税率。
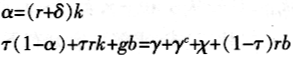
得到r=0.11，τ=0.217。
在消费者进行最优化选择时，如果存在着内点解，则以下条件得到满足
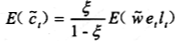
而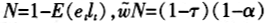
由资源约束条件，我们得到
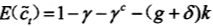
于是，我们得到ξ=0.2826。
在这些参数设置的基础上，我们通过市场均衡条件得到=0.9939。
总之，我们采用的参数列举如下：α=0.6，δ=0.0665，g=O.07，χ=0.022，γc=0.0853，γ=0.06，υ=1.5，β=0.9939，ρ=0.8，σ=0.06，ξ=0.2826
(二)计算方法
我们采用matlab软件进行数值模拟计算。对于劳动生产力的马尔可夫过程，我们采用广为采纳的方法，即Tauchen(1986)的做法，将其离散化为7个状态空间。
在我们采用的次优框架下，福利分析相应于每个债务负担率水平下的比较静态分析。即在给定的政府政策变量下，计算均衡时我们采用如下方法。在给定一个经济增长率水平和劳动者的休闲水平(可以得出市场对劳动时间的需求)，我们可以资本存量的相对水平(相对于产出，下同，可以简单称之为资本的需求水平)和工资水平，然后根据政府的预算平衡方程，我们得到税率水平。在此基础上，我们采用值函数叠代的方法求解动态规划方程，从消费者的最优化决策得到消费者对资产的供给水平和对劳动时间的供给水平。如果这两个供给和需求水平各自相等，那我们就得到了均衡的经济增长率水平和休闲水平，进而计算此时的福利水平。如果这两个市场没有同时达到均衡，那么我们需要改变经济增长率和休闲水平，直至两个市场达到均衡为止。
四、数值模拟结果
(一)福利评价标准
我们在具体经济的模拟中，由于在效用函数中，涉及休闲与劳动的替代，因此，我们需要固定或休闲其中一个要素，然后进行福利比较。为了跟没有休闲的效用函数比较，我们采用的标准是固定休闲。即通过我们得到的样本经济模型的数值与其他债务存量下的福利值，固定样本经济的休闲，通过这两个福利值换算出消费的福利收益或损失。即若样本经济下均衡的消费和休闲流为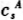
和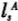
，稳定分布为λA，而另一经济的消费和休闲流为
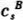和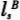
，稳定分布为λB，假定从样本经济变为B经济的福利收益为u。则
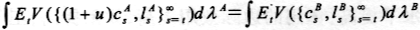当u＞0时为福利收益，反之为福利损失。
(二)福利结果
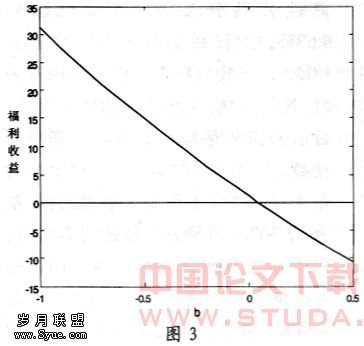
在参数化的基础上，我们改变政府债务存量得到相应的福利值，进而我们进行最优债务分析。我们采用的福利基准为样本经济状况(1978—1998年这一经济阶段宏观经济的福利状况)。以此为参照，我们列举出债务存量从—1到0.5水平时的福利变化、消费比率(消费占产出的比例)、工作时间比率、利率、税率和经济增长率。从数值计算结果我们发现，在中国的经济参数下，政府公债的自我保险作用较小，不足以抵消公债提高造成的挤出效应和征收比例税造成的税收超额负担，最优的债务存量为负值。从我们得到的结论来看，福利收益或损失比Aiyagari和McGrattan(1998)要大很多，他们的结论从0到67%的债务存量变化的福利损失或收益还不到0.1%，而林细细和龚六堂(2007)则在外生技术进步的经济中得到，相比样本经济，当债务存量由样本经济水平提高到50%时，福利损失则仅将近1%。但是我们得到的福利情况则是如果将债务存量由样本经济提高到10%时，福利损失为1.4616%；20%的债务存量比例时，福利损失为3.9746%；到50%的债务存量时，福利损失为10.6233%。这些结果我们在图3中反映出来，在该图中，福利值的单位为1%，福利收益为0处，即样本经济处我们用一横线标出。从这些福利值来看，提高债务存量需要相当谨慎，因为其福利影响实在太大，因此有必要对我国政府公债政策进行足够的关注。
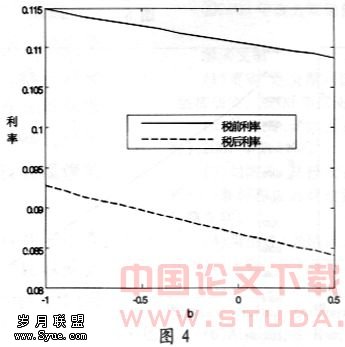
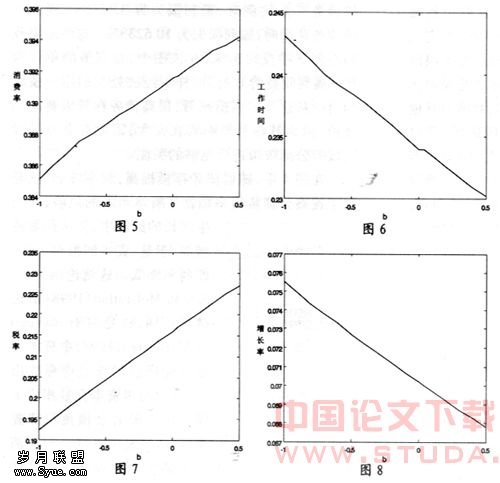
在图4中，随着债务存量提高，利率降低，这是由于提高公债负担率加剧了资本市场的风险，在内生增长的经济中，资本积累将增加，于是，资本回报率下降，即利率降低。这结论跟Aiyagari和McGrattan(1998)结论截然不同，这是由于Aiyagari和McGrattan(1998)中资本市场不能通过增长效应释放出来，因此使得资本存量相应下降。由于随着公债负担率提高，经济增长率下降，于是，消费者的收入拿去补偿经济增长的资本将减少，这增加了当期消费，于是消费率提高，这在图5中得到反映。而随着消费水平提高，休闲的边际效用提高，休闲提高，工作时间减少，图6也反映了这种关系。图7表明政府债务存量提高，税率增加。因为债务提高从政府预算角度来看意味着政府需要收取更多的税收，故税率相应提高。与我们前面的理论分析保持一致，提高政府公债存量降低经济增长率，我们从图8中直观地得到这一结论。
为了更好地理解我们结论的可靠性，我们将在下一部分进行敏感性分析，即改变我们模型所依赖的参数，理解这些参数变化导致的福利影响。
(三)敏感性分析
我们在本部分主要考虑我们得到的结论对于参数的敏感性。即我们假定除了主观贴现因子和我们需要的参数外，其他参数保持不变，当参数发生变化时，通过主观贴现因子调整使得其他经济变量符合样本经济，各种结果我们在表中列举出来。
首先，我们改变经济增长率和资本份额的敏感性。如果将样本经济的经济增长率提高到8%水平，我们发现，样本经济的增长率增加，与样本经济下同等债务水平引起的福利损失相比，其数值将较大。而资本份额下降，也有同样的效果。在表1中我们列举出资本份额降低到0.55水平的情况。从这些数值来看，这两个参数具有一定的敏感性，我们看到最大的福利损失不会超过10%。
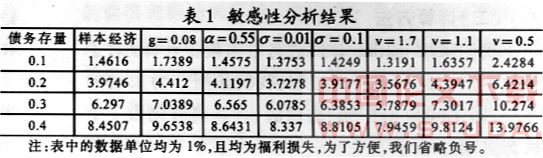
其次，我们变动劳动生产力的波动，我们选取标准差为0.1和0.01两种情形，从表1中，我们发现，这些波动的相比而言敏感性较差，跟样本值差别不大，稳定性较好。
最后，我们考虑风险回避系数的敏感性。我们分别取值为υ=1.7、1.1和0.5。我们发现风险回避系数的敏感性也是比较大，但是基本没有超过10%。
(四)政策分析
从数值模拟的结果，我们得到在考虑了政府公共开支对生产产生影响的内生经济中，政府公债存量水平的变化对福利影响极大。相比样本经济，债务存量增加到10%时，福利损失约为1.5%；而提高到20%，则福利损失约为4%；30%时，福利损失则为6%；40%时，福利损失约为8%。总之，债务存量每提高10%，将产生2%左右的福利损失。因此，对公债大量发行的恐慌是有必要的。
那么，究竟我国从1998年开始以来实行的积极财政政策，公债发行幅度增加导致公债存量上升会造成多大的福利影响呢？为了更为准确地研究这个问题，我们把改变了的财政政策详细考虑进去。我们注意到：1999-2004年，政府的消费性公共开支和转移支出发生了一定的变化，消费性公共开支从8.53%增加到8.63%，而转移支出从2.2%降低至1.07%，当我们把这个因素考虑进去时，我们发现，相比原先的样本经济，目前的债务存量水平能够带来福利收益，而且福利收益较大，相比维持在4.32%的债务存量水平，福利收益为17.36%。而债务存量达到20%时，则还有12.31%的福利收益，即使债务存量水平达到40%，其福利收益为6.94%。总之，单纯考虑转移支付和政府消费性公共开支变化后的债务存量水平发生变化的福利影响时，我国目前大规模的发行公债相比以前而言，则仍然是一个较好的帕累托改进，有较大的福利收益。
但是，我们不能忽略一个事实：1999年以来，我国政府的生产性公共开支比重急剧下降，1999至2004年生产性政府公共开支下降至3.731%。由于政府生产性公共开支影响经济的内生增长率，生产性公共开支减少将导致经济增长率急剧下降至4%，而然，社会福利也将发生巨大的变化。在与样本经济同样的债务存量水平下，目前的财政政策的福利损失则达到87.49%——如此巨额的福利损失！不过我们发现在这种经济下，改变债务存量造成的福利损失不是太大。如相比样本经济，当债务存量达到40%时，福利损失也仅为88.2633%。即改变债务存量水平而保持其他财政政策不变时的福利损失不超过1%。于是，在这种经济中，政府改变生产性公共开支要相当谨慎，因为这种增长效应(growth effect)有时会很大。不过，这与目前社会上一直呼吁的政府公共开支过大并不矛盾，因为那主要是针对于政府白白浪费在消费性公共开支上和生产性公共开支效率低下而提出的。
五、结论
本文的主要贡献是在Aiyagari和McGrattan(1998)的理论模型基础上，考虑了生产性公共开支对经济增长的影响。在此基础上，我们利用中国的经济参数进行实证分析，结果发现，在中国，尽管巴罗—李嘉图等价定理不能成立，这为存在最优公债提供一个合理存在理由，但是比较公债的正负效应，我们发现最优公债仍然为负。由于我们的目标放在目前中国讨论较多的大规模发行公债问题，因此我们主要集中在样本经济(1978-1998)基础上，讨论公债水平发生改变后带来的福利影响。而由于生产性公共开支将产生巨大的增长效应，政府公债提高降低了经济增长率，这产生很大的负福利效应，这一结果与Aiyagari和McGrattan(1998)、林细细和龚六堂(2007)差别较大，政府目前较大规模的发行公债需要相当谨慎！
而且假如我们将变化的政府开支和转移支出考虑进去，我们发现，其实目前的公债规模相比以前的样本经济，其福利损失将更大，达到87%以上！因此，我们有必要将大规模发行公债视为洪水猛兽。
但是，本文仍然存在着一些需要改进的地方。首先，我们没有考虑国债的利率期限结构，而这问题则是目前讨论较多的一大热点，如果将利率期限考虑进去，其福利影响将是如何？其次，我们考虑的是一个封闭经济的情形，如果拓展到开放经济，在经济大国和经济小国中，债务存量的变化又将带来怎样的福利影响？最后，假如我们进一步考虑分级财政，中央政府和地方政府都能发行公债，那结果又将如何？尽管中国目前没有地方政府发行公债，假如我们能够提出一些合理的理论解释，则将为地方发行公债与否提供一个较好的理论依据。
