商业银行隐含期权的利率风险管理研究
关键词：隐含期权，利率风险，有效持续期，期权调整利差模型
一、引言
隐含期权是指有期权选择性质但不具备公开的期权合约形式。商业银行资产的隐含期权主要是指可提前赎回期权，它带来的利率风险是借款人的提前偿付风险。例如抵押贷款，银行允许贷款持有者在贷款期到期日之前以某一价格提前偿还贷款，银行实际上向借款人出售了一个美式买入期权。负债方面的隐含期权是可提前回售期权，它造成的利率风险是客户随时取款的风险。例如允许大额的存单或定期存款的所有者在存款到期日之前以某一价格提前收回现金，实际上相当于银行向存款人出售了一个美式卖出期权。因此具有隐含期权的资产负债可以看作是相应的含权的固定收入证券的组合。在价值上，隐含买入期权证券的价值等于无隐含期权证券的价值与买入期权价值之差，而隐含卖出期权证券的价值等于隐含期权证券的价值与卖出期权价值之和。
麦考莱持续期和凸度是衡量利率风险的基本方法。F.R麦考莱(1938)为了评估债券的平均还款期限，定义了“持续期”，它最初用来表示平均还款期限，即通过衡量债券的平均到期期限来研究债券的时间结构，持续期越长，利率风险越大。Toevs A L， Haney W C(1986)认为当利率变化较大时，基于持续期的利率风险测量就会产生较大的误差，因而提出基于凸度的风险测量方法。但是麦考莱持续期和凸度没有考虑隐含期权对资产负债价值的影响。于是弗兰克.J.法波齐(Frank fabozzi，1986)提出基于期权调整的有效持续期和有效凸度的模型。 L.S.Hayrel(1990)进一步分析后认为引进了隐含期权后，资产负债项目可能面临负凸度和更大的凸度不匹配风险，如果运用期权调整利差模型来管理此类风险则是一种崭新的考虑。
我国由于长期处于利率管制状态，银行从不考虑隐含期权，现行研究也主要集中在商业银行的重新定价风险上，并且以敏感性缺口分析为主要的衡量技术，对于隐含期权的利率风险还没有引起足够重视。随着我国利率市场化进程的加快，商业银行亟需对含有隐含期权的资产负债项目进行利率风险管理，否则“忽视隐含期权会造成持续期缺口，从而对机构的权益造成较大损失”(Brooks and Gup，1997)。
二、隐含期权的利率风险衡量指标
衡量利率风险的基本方法是麦考莱持续期和凸度，，但是麦考莱持续期和凸度模型假设的是所有资产和负债的现金流量不随利率变动而变化，而具有隐含期权的金融工具的未来现金流会随利率波动而变化，使得麦考莱持续期缺口模型无法处理具有隐含期权的利率风险问题。有效持续期和有效凸度认识到(Frank fabozzi，1986)，随着利率的变化，与其未来现金流会发生变化，债券价值表现也会受到影响，它直接运用于以不同收益率曲线变动为基础的证券价格，这些价格反映了证券中隐含期权价值的变动。有效持续期和有效凸度可用下式进行：
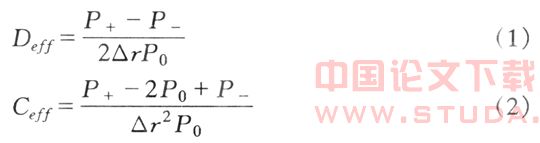
其中：Deff和Ceff分别代表有效持续期和有效凸度；△r是利率的变动，用于计算P0和P±，在此为100个基本点；P0代表债券的初始价格；P-，P+代表收益率减少或增加x个基点时债券的价格；R-，R+代表初始收益率R减去或加上x个基点，而初始收益率是指金融工具的初始到期收益率，对于隐含期权的金融工具来说，它由无风险市场利率加上期权调整利差构成。
期权调整利差(Option-Adjusted Spread，简称OAS)是20世纪80年代初随着美国资本市场上住房抵押贷款证券化的出现而出现，它是指相对于无风险利率的价差，通常以基点的方式进行度量，一般以国债即期利率曲线(或同一发行人即期利率曲线)为基准，在此基准水平上浮动一定利差，综合考虑利率的波动，将期权调整后的现金流进行贴现，得到含权债券的理论价值，最终使理论价值等于市场价格的利差水平。因此，OAS是对金融工具中含有期权风险的补偿，是一个综合考虑了期限结构和隐含期权的收益率指标。从有效持续期的计算公式中可以看到，OAS的计算是衡量隐含期权风险的基础。其计算式为：
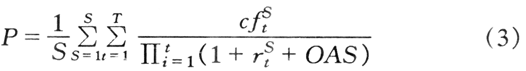
其中：S为利率变动方式的数量；cfSt为在第S种方式下t期的现金流量；rSt为在第S种方式下t期的国库券利率；P为市场价格。但要注意的是1／S是一种概念的表达形式，它所代表的平均不是数学平均或是几何平均，而是风险中性概率测度下的均值。
从数学上理解，OAS是在每一条模拟利率路径中，对未来t时刻现金流进行贴现加总得到的现值，这个价格也称作“特定路径的特定利差价格”，各条路径现值的均值即为含权债券的理论价值，由于该理论价值往往不会等于含权债券当前的市场价值，因此需要对当前的整条利率期限结构统一进行平移，OAS值是通过单变量求解使得理论价值等于市场价格的平移量。从技术上理解，OAS是用来估计资产总收益和所有模拟的利率情景库券收益之间的差值，它代表了一组风险组合，包括隐含期权风险、信用风险、流动性风险等，但是，此处假定资产或负债具有与基准相同的信用等级和流动性风险，所以只考虑隐含期权风险。
因此，OAS模型的核心是进行大量的利率情景制造。对于商业银行而言，要衡量资产和负债的隐含期权风险，选择适合的利率情景模型和方法并对资产和负债的价值进行估计是运用期权调整利差模型的主要目的和关键。利率情景的制造需要确定瞬时利率遵循的随机过程。所有可能发生的利率路径不但要遵循假定的随机过程，而且还要符合现实的初始期限结构。一旦确定了利率情景，再根据本金和利息的摊销计划以及行为模型，则每一情景和每一时期的现金流量也可以随之确定。利率情景制造的主要方法有三叉树法和蒙特卡罗模拟法。
三、资产或者负债有效持续期的模拟计算
蒙特卡罗模拟法需要借助计算机进行模拟，本文用三叉树模型来分析利率情景的制造，以及有效持续期的演算过程。用三叉树计算有效持续期的具体步骤为：估计利率的三叉树动态树图，计算证券的OAS；将利率期限结构上升(下降)少量固定的基点，在此基础上重新估计利率的三叉树图；给三叉树图上的每个短期利率加上OAS得到“调整后的三叉树”；使用“凋整后的三叉树”计算调整后的债券价格；计算有效持续期。
Bierwag.D(1977)在研究不同利率期限结构随机变动的持续期计算方法中提出并使用了的经典初始利率期限结构模型：
这里的R(m)是m年的零息票债券的即期利率，设β为0.5，这意味着30年的利率比1年的利率要高1.7%，将λ值设为0.06，并将该资产的初始利率结构模型设定为：
它代表的是一条斜向上的收益率曲线。为了问题简化，在这里将这个模型就作为初始收益率曲线。下面以一项假设的一年期贷款为例计算其有效持续期和有效凸度。可将该贷款看作是一项可赎回债券，假设利率变动的时间增量为0.5年，面值为100，短期利率遵从下列过程：dr=[θ（t）-ar]dt+σdz，并假设利率均值回复率(α)=0.05，利率波动率为(σ)=0.015，△t=0.5。
根据利率情景制造理论：
1.84%，r*(0，0)=0，一般情况下选用I型即标准型三叉树，两期的三叉图如图1：
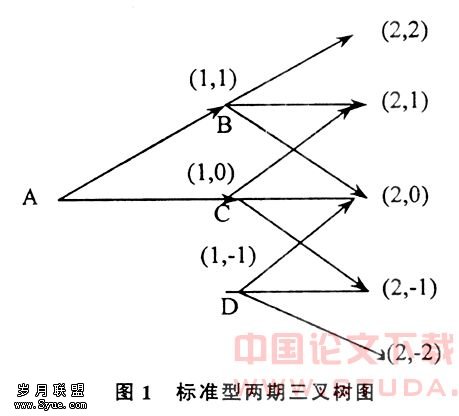
则r*(1，0)=0，r*(1，1)=1.84%，r*(1，-1)=-1.84%，根据SHU3三叉树分支概率的计算公式可得：
在节点(0，0)处，即A点处(i=0，j=0)，pu=0.167，pm=0.666，pd=0.167；
在节点B处，即i=1，j=1，puu=0.160，pum=0.667，pud=0.173；
在节点C处，即i=1，j=1，pmu=0.167，pmm=0.666，pmd=0.167；
在节点D处，即i=1，j=1，pdu=0.173，pdm=0.667，pdd=0.160；
根据三叉树相关公司，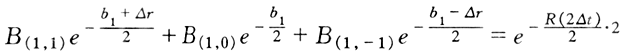
且R(2△t)=R(1)=6%，R(3△t)=R(1.5)=6.2%，代入上式，可得：b1=6.32%，
再根据已得的B(1，1)，B(1，0)，B(1，-1)以及各期分支的概率可求得:
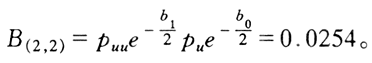
同理可得：B(2，1)=0.2092，B(2.0)=0.473，B(2，-1)=0.2092，B(2，-2)=0.0254
再根据三叉树相关公式，可得类似公式：
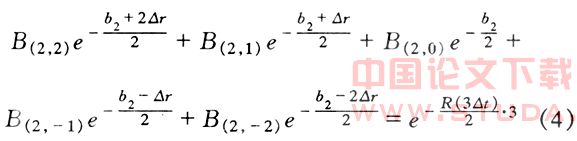
于是，b2=6.69%
由此可以求得：
以上过程是通过初始的期限结构推算出未来利率的市场预期，即远期利率，构造出利率厂的可能变动路径(如图2)。
接下来则根据倒推法计算OAS值、有效持续期和有效凸度。
将该可买入资产看作是一个隐含买入期权的两期平价证券，且面值为100(Vc)，息票率为i。根据对隐含证券估价的原理该证券在发行后即可以行使买入期权，其对应的利率树图由两个时间段构成。该证券的持有者1时刻和2时刻分别可以收到Vci和Vc(1+i)的现金流。期权的价值等于立即执行期权的价值(NCS0-Vc，NCS0是无隐含期权下，证券在时刻0的现值)与下一刻执行的价值的现值之中的最大值，即：
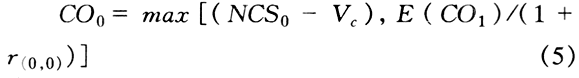
其中CO0代表买入期权在时刻0的价值；E(CO1)表示在2时刻行权的期权价值在时刻1的期望值。
由于是两期证券，所以期权只可选择在1时刻执行或是不执行，1时刻为期权执行的唯一机会，所以在该证券中CO在1时刻的价值为：
CO(1,j)=max[NCS(1,j)-Vc,0]j=-1,0,1
NCS(1,j)=Vc(1+i)/(1+r(1,j))
由于隐含买入期权的证券价值等于无隐含证券的价值与买入期权的价值的差，所以该证券在初始 0时刻的价值(CB0)为：
CB0=NCS0-CO0=100
根据以上步骤算得：i=11.12%，
所以c=／2=5.56
根据OAS的计算公式(3)展开后可对两期的 OAS值进行计算：
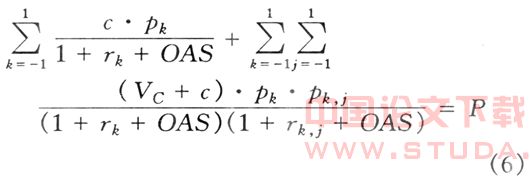
式中：k，j分别代表在第1、2时刻，利率变化的三种方式，1，0，-1分别代表上升、持平和下降。根据以上得到的所有数据，通过Excel的单变量求解得到该两期证券的OAS值为232个基本点，意味着含有隐含期权的资产所应得的风险补偿。
接下来再根据收益变动基点，将上式中的rk，rk,j加减同样的基点数，得到收益率上升和下降时的证券价格，再套用有效持续期的公式即可得出。假设收益率变5个基点，即0.05%，根据上式可得收益率上升和下降对应的市场价格分别为：
如果收益率变动1%，则该贷款用有效持续期和凸度解释的价格变化百分比分别为：
-0.92×0.01=-0.92%,0.5×(-85.5)×(0.01)2=-0.43%
由于具有隐含期权，所以该贷款的有效凸度为负，并且负的凸度会加大该资产对利率的敏感性。
如果是对一笔定期存款计算有效持续期其计算过程大致相同，所不同的是存款使用的初始期限结构与资产的可能不同，另外定期存款的期权性质相当于可回售证券，所以含权的定期存款价值为无隐含期权下定期存款的价值与期权价值的和。
四、隐含期权条件下的利率风险控制策略
1.从契约上防范隐含期权利率风险。当不能对隐含期权利率风险进行预测和度量时，银行可以通过构建提前偿付风险的防范机制对隐含期权利率风险进行事前控制。在论述隐含期权利率风险来源时阐述过隐含期权通常来源于商业银行的契约中，因此也可以通过契约的方式来防范隐含期权风险，即在与客户签订协议时，就加入有关对提前偿付的违约责罚条款，这也是一种对贷款人权利的保护制度。
2.运用证券化技术转移隐含期权利率风险。近年来随着资产证券化的快速，为商业银行转嫁隐含期权利率风险提供了一条新途径。在处理隐含期权的问题上，银行也可以考虑将具有隐含期权风险的资产和负债整体打包转让给SPV，即通过证券化的方式，资产和负债的信用风险和隐含期权利率风险都随之转移给了SPV，SPV进而通过证券的发行在资本市场中将这些风险转移给更多投资者。
3.建立基于期权调整利差模型的利率定价机制。该模型对内是商业银行通过期权调整有效持续期衡量资产或负债的利率风险的模型，对外则是银行与客户商议贷出或借入资金的定价模型。在确定银行贷款利率时，参照银行资产业务中隐含看跌期权的价值调高贷款利率；在确定存款利率时则根据隐含的利率看涨期权适当调低存款利率水平。只有经过这样的利率调整，商业银行才能对由隐含期权增加的利率风险进行补偿，从而维护银行的利益，并作出最有竞争力的定价决策。
4.匹配有效持续期。为了将利率风险控制在一定范围内，可在计算有效持续期和凸度的基础上，对资产和负债的隐含期权风险进行对冲：(1)在资产隐含买入期权而负债隐含卖出期权的条件下，配置一定量的隐含卖出期权的资产与隐含买入期权的负债，使前者的负凸度缺口得以同后者的正凸度缺口对冲。(2)分别计算无隐含期权的资产负债的持续期和有隐含期权的资产负债的期权调整持续期，再分别计算所有资产和负债的加权平均持续期，从而选择各种满足持续期匹配要求的资产负债的期限组合，将持续期缺口控制为零或约等于零，达到有效持续期的免疫。(3)在满足持续期匹配要求的资产负债的期限组合中选择凸度缺口最小的组合，发行结构性票据即是一种有效途径。
5.引入利率衍生工具全面控制利率风险。利率衍生工具不仅可以被运用于弥补敏感性缺口管理等传统表内技术的局限性，对于含有隐含期权的资产和负债的利率风险管理同样适用，银行可以针对具有隐含期权的资产或负债进行套期保值以对冲或是消除行权可能造成的损失。比如利率期权不仅能消除预期利率不利变动的影响，而且还不会丧失利率有利的波动可能给银行带来的盈利。
五、结 论
隐含期权通常内含在商业银行资产和负债业务的契约内，容易被忽视。本文依照利率管理的一般过程，对隐含期权利率风险的识别、衡量和控制进行分析后，可以得出如下结论：(1)通过对商业银行资产负债项目进行分析，得到银行的存款业务和贷款业务都普遍存在隐含期权。(2)在对隐含期权下的利率风险进行衡量时，不宜使用敏感性缺口分析和修正持续期缺口分析，而应采用有效持续期和有效凸度作为衡量指标，才能将利率变动引致资产负债价值变动的过程在有效持续期计算过程中得以体现。(3)在对具有隐含期权的工具的利率风险进行衡量时，不能忽略凸度的影响。(4)需要从契约限制、风险定价、风险转移、表内控制技术和表外控制技术五个方面共同构建隐含期权利率风险的控制机制，实现利率风险的全面控制。
