国内上市公司可转换债券定价实证分析
内容摘要:本文考虑了可转换债券隐含的转股、赎回、回售等条款,借鉴二叉树模型和Black-Scholes公式对沪深市19只转债进行实证研究,发现目前国内可转债存在不同程度的低估并分析原因。
关键词:可转换债券 期权 二叉树模型 Black-Scholes公式
可转债是一种复合工具,因而可转债的价值特征特别复杂,可转债定价是金融工程中有挑战性的课题之一。可转债作为股权融资的补充,对于完善国内证券市场投资品种、进行积极的金融创新有重要的意义。
可转债定价模型
目前国内对可转债研究都是基于小样本,而且时间跨度不超过一年甚至仅为一天的结果,最长仅为3个月。本文研究的是2002-2004年市场上的19只转债的日交易数据,对于2004年发行的暂时没有纳入。所有转债数据不做特别说明均来自北方之星公司开发的阿尔法数据服务系统。本文采用两种模型,其一是分解模型;其二是二叉树定价模型。通过研究发现转债价格不同程度地被低估。
分解模型
分解模型将可转债分解成两部分——一个普通的公司债券和一个关于标的股票的看涨期权,债券部分采用贴现因子模型,看涨期权定价采用Black-Scholes定价模型。分解模型由于量小,方法简单,也是目前实务界常用的方法,但是转股权和普通意义上的看涨期权并不完全一样,因为转股价随着转债触发条件而不断修正,由于Black-Scholes适用于欧式期权,但是可转债的转股权是路径依赖的美式期权,可以提前执行,一般国内转债的封闭期只有半年(少数也有一年)。而且这种方法忽略了转债中隐含的赎回权和回售权。
二叉树模型
为了克服分解模型的缺陷,本文还采用了Cox、Ross和Rubinstein(1979)提出的二叉树定价模型来对转债隐含期权定价,考虑到运算效率和精确性,可取步长为100。并将风险调整利率纳入二叉树的计算中。在二叉树每一结点,考察以下几个因素,现逐一说明:
(1)终点条件(Endnode Condition),即CT=Max(nTST,λPar),其中CT是转债到期时刻T的公平价值,ST为T时刻标的股票价格,nTST为转股价值,λ为持有转债不转股到期利息补偿比率,Par为转债面值。
(2)转换价值边界(Convertion Value Boundary),在转股期内,可转债公平价值一定高于转换价值,否则就存在套利机会,因而:
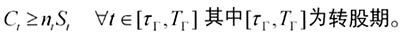
(3)赎回边界(Call Boundary),也称为强制转换条款,即当股价满足触发条件ρ时,发行人有权按照条款约定的价格赎回部分或者全部的债券。即:
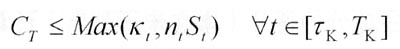
kt是t时刻的赎回价格。
其中Pt为t时刻的赎回价格。

在二叉树的每一个节点,判断转债价值是否达到条件(2)、(3)、(4),然后根据Brennan和Schwartz(1980)提出的发行人最优赎回策略和持有人最优回售策略,决定是否执行期权。
(5)利率及信用风险,由于可转债既有股票特性又有债券特性,它的价格也受发行公司的信用风险影响和利率的影响,Brennan和Schwartz假定利率服从均值回复模型,Ho和Pfeffer假定利率服从Ho-Lee模型。由于国内发行的转债一般都有银行提供担保,因而本文认为转债和普通公司债券具有相同的信用风险,故采用相同期限企业债的到期收益率作为可转债的贴现因子。
样本选取
为了样本的代表性和数据完整性,选取19只转债的日收盘价格数据,时间跨度为2002.1.1-2004.8.31。
按照前面介绍的二叉树方法,用Matlab7.0编程,输入变量有:
K0为转股价格,St为t时刻股价,Rf为无风险利率,本文取一年期存款利率Rf=1.98%;持有到期利率补偿、赎回边界、回售边界、发行时间和到期时间、转股封闭期根据各个转债的相关条款,二叉树步长设为100步。程序中还有两个重要输入变量即股票的波动率和贴现率。对于波动率,用ARMA(1,1)回归股价的(复权后)对数收益率的条件均值,再利用GARCH(1,1)回归其条件方差,即:ht=α0+α1r2t-1+βht-1,其中α0、α1、β为待估参数,ht、ht-1为本期和前一期条件方差,利用SAS9.0中的Autoreg过程可以出。对于贴现率,根据前面分析,由上交所每天交易企业债隐含的到期收益率,采用三次样条函数拟合。
综上所述,可发现可转债存在比较严重的低估;出现转债价格被严重低估的主要原因如下:目前国内的转债条款设计太复杂;我国证券市场上的投资者尚未成熟;目前市场上还没有有效可转债定价体系;的证券市场机制不完善。目前我国证券市场缺乏卖空机制,股票还不能卖空,即使模型推导中出现无风险套利机会,也无法实现的,这使得模型推导的前提条件难以成立,因而也是最重要的原因。











