交易所国债回购利率期限结构研究
关键词:利率期限结构,预期理论,国债回购
引言
目前对市场的监管过程中,对利率期限结构的关注日益增多,这主要由几方面因素决定的:首先,国外学者运用一系列指标进行大量的实证研究表明,利率期限结构的斜率对于经济未来时期内的变化具有一定预测作用,如Estrella和Hardouvelis(1991)的研究表明,一个向下倾斜的期限结构往往伴随着未来经济增长的减慢甚至衰退,Bernanke(1990)、Harvey(1991)、Kamara(1997)以及Gerlach(1997)对发达国家金融市场与经济的关联性研究也得到了类似的结果;其次,期限结构的斜率对未来通货膨胀变化具有一定的预测作用,Mishikin(1991)、Jorion和Mishkin(1991)以及Gerlach(1997)的研究都证明了这一点,即一个向上倾斜的期限结构往往意味着预期通货膨胀率的上升;最后,对于货币政策制定者来说,利率期限结构包含有市场参与者对未来短期利率走势的预期。值得注意的是,尽管经济理论认为长期利率受到预期的未来短期利率的影响,但是其他因素对期限结构的影响也是不容忽视的。例如,市场流动性的变化和市场参与者对持有不同到期期限的金融产品所承担的风险做出的估计,都会影响到利率的期限结构。如果这些因素的影响是时变的,将使得对期限结构的解释更加复杂。
传统的期限结构预期理论认为,期限风险溢价是不随时间变化的,且长期利率仅由预期的未来短期利率变化决定。就目前国内学者的研究来看,唐齐鸣,高翔(2002)和史敏(2005)等的研究发现,在常数期限溢价的条件下,我国的利率期限结构在亚洲金融危机发生前符合传统的预期理论,但随后的样本期内不能给予预期理论以充分的支持。本文通过对我国交易所国债回购市场1997年9月1日——2006年12月31日期间的周数据进行实证研究,试图发现在亚洲金融危机发生后,我国的利率期限结构能够在多大程度上解释未来短期利率变化。与之前国内学者的研究结果不同之处在于,文章首先拒绝了预期理论中期限风险溢价为常数的原假设,在此基础上引入了时变的期限风险溢价,使用广义矩估计法对预期理论进行再检验,发现其对未来短期利率的变化具有显著影响,且Wald检验认为在时变的期限风险溢价条件下,未来短期利率的变化与不同期限的利率差具有完全的正相关性。
本文结构如下:第二部分对期限结构的传统的预期模型进行简要介绍;第三部分对7天、14天、28天、91天和182天的交易所国债回购利率及各期利率相对于7天期利率的利差进行初步的统计分析,通过GMM方法对样本期内的数据进行实证研究,发现期限溢价为常数时不支持预期理论,但加上随时间变化的期限溢价时却不能拒绝预期理论;第四部分得出结论,认为随时间变化的风险溢价可能在对利率的预期理论进行检验时起到非常重要的作用,且在风险溢价时变的情况下,交易所国债回购利率符合预期理论。
预期理论模型与广义矩估计
一、利率期限结构的预期理论模型
期限结构的预期理论认为,投资N期的预期收益等于未来投资于一系列即期利率得到的预期收益加上一个期限风险溢价,且溢价不随时间变化。令R(N)t为N期的即期利率,则预期理论用公式可以表示为:
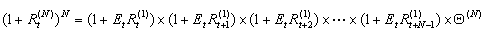 (1)
(1)
式中,Θ(N)表示期限风险溢价,用小写字母表示连续复利(即r(N)t=ln(1+R(N)t)),并定义θ(N)=lnΘ(N),可以得到:
 (2)
(2)
式(2)两边同时减去r(1)t并整理,得到:
 (3)
(3)
对(3)式进行简要的经济意义解释,考虑最简单的情形N=2,此时:
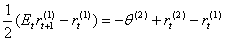 (4)
(4)
假定期限风险溢价为0,则式(4)表示预期1期即期利率的变化Etr(1)t+1-r(1)r与利率差r(2)t-r(1)t呈线性关系。因此,如果预期短期利率上升(下降),期限结构将上倾(下倾)。同时,式(4)表达了期限结构对预测未来通货膨胀与经济活动的重要性。假定中央银行将上调利率以抑制通货膨胀进而降低经济增速,如果市场参与者确信通货膨胀率将上升,那么他们也会认为中央银行会在近期上调利率。根据式(4),这意味着较长期限(这里相对于短期来讲的,本文指7天期交易所国债回购利率)的即期利率在本期已经开始上升。如果平均来看市场参与者对经济增长的估计是正确的,我们将会在本期看到一条上倾的利率曲线,并伴随着未来时期内较高的即期利率和较低的经济增长速度。
如果预期是理性的,那么定义: ,其中
,其中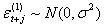 且独立同分布,则式(3)可以写为:
且独立同分布,则式(3)可以写为:
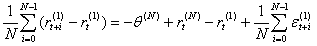 (5)
(5)
由此可以得到检验预期理论的回归方程:
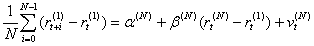 (6)
(6)
V(N)t为N-1阶移动平均误差,故本文采用广义矩估计来进行回归检验,避免了之前国内学者在分析过程中造成的估计偏误。预期理论认为此时应当满足:α(N)=-θ(N)且β(N)=1。
二、广义矩估计(GMM方法)
Hansen在1982年提出了GMM方法用以解决一大类计量模型的估计与检验问题。这种方法的思想是用样本的矩条件代替模型的矩条件,进而参数的估计值就利用使一个样本矩的加权二次式最小化而得出。其表达为:在一个计量模型中,
Yt=a+BXt+Ut,t=1,…,T (7)
Yt、Xt和Ut是N维向量,设定θ是一个计量模型的q维向量的模型参数,Ut(θ)是N维向量的模型干扰项,Zt是L维向量的工具变量,通常包含一个常数、Xt和它的过去值及Yt的过去值。这样,我们把方程(7)的矩条件写为:
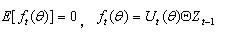 (8)
(8)
其中Θ为克罗内克乘号,它使ft成为一个有NL维向量的矩阵函数。设gt是ft的样本均值: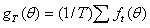 ,那么要得到参数的估计值,只要找到θ,使得
,那么要得到参数的估计值,只要找到θ,使得
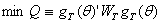 (9)
(9)
WT>0是一个NL×NL正定加权矩阵,结果得出的θ估计值就是GMM估计值。假定方程的零假设是rank(B)=K,我们有B=AC,存在N×K矩阵A和K×M矩阵C,所以我们只需要估计(α,A,C),为保证估计值的唯一性,对A实行标准化得到A′=(IK,A2),设θ=vec(a,A2,C),在系数空间上通过解(9)式就可得到唯一的GMM估计值。
预期理论的实证检验
一、样本选取及统计特征
本文选取我国上海证券交易所国债回购市场利率数据,时间跨度为1997年9月1日至2006年12月1日共458个交易周,共5组数据(7d,14d,28d,91d,182d),数据来源于红顶软件。从图1中看到,交易所国债回购利率在1997年和1998年的两年期间呈大幅下降趋势,且波动幅度较高,随后缓慢下降且波动幅度减小,已经从1997年9月的10%左右下降到现在的2.3%左右。另外在样本期内,短期回购利率大于长期回购利率的情况也多次发生,笔者认为这一现象部分与股票一级市场的IPO有关,在新股发行当天,大量资金涌向A股一级市场,导致市场资金短缺,使反映资金松紧的国债回购短期利率居高不下。
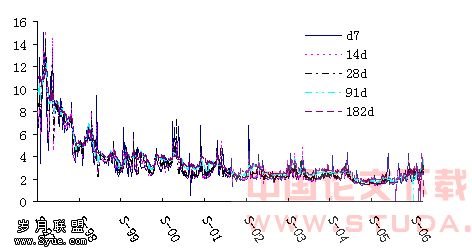
图1 交易所国债回购利率
表1给出了较长期限利率与7天回购利率的利差的简单统计特性及单位根检验。由表中结果可知,回购利率平均利差及波动幅度均随期限延长而增大,且ADF检验表明各期限利差均为平稳过程。
表1 各期限利差统计特征及单位根检验
利差 | 14d-7d | 28d-7d | 91d-7d | 182d-7d |
均值 | 0.0273 | 0.115 | 0.3344 | 0.470 |
最大值 | 2.63 | 4.108 | 5.705 | 6.855 |
最小值 | -4.61 | -6.142 | -5.312 | -5.056 |
标准差 | 0.693 | 0.875 | 0.946 | 1.021 |
ADF检验 | -24.128* | -15.568* | -16.963* | -16.348* |
注:选择带常数项但无趋势项的ADF检验,滞后阶数由AIC和SBC准则确定,*表示在5%水平下显著
二、期限风险溢价为常数时的预期理论检验
我们使用GMM方法对前面得到的式(6)进行估计,标准误差项通过Newey和West(1987)提出的方法得到,因此,回归分析中同时考虑了误差项的异方差性及MA(N-1)过程。结果见表2。由结果可知,在14天、28天与7天期的利差检验中,方程拟合度较低,且Wald检验表明β系数在5%置信水平下显著异于1;91天、182天与7天期的利差检验表明,方程拟合度较高,且Wald检验表明在5%置信水平下不能拒绝β=1的原假设。另外,除14天、28天利差的回归方程外,期限风险溢价均显著为负。总体来看,亚洲危机之后,在常数项期限风险溢价的条件下,利率期限结构的预期理论不能得到充分支持,这与史敏(2005)的结果是一致的。
表2 GMM对式(6)的估计结果
利率期限 | α(N) | β(N) | Wald检验 |
|
14d | -0.020 [0.020] | 0.611* [0.295] | 0.013* | 0.163 |
28d | -0.112 [0.128] | 0.852* [0.147] | 0.032* | 0.255 |
91d | -0.486* [0.087] | 1.218* [0.158] | 0.170 | 0.710 |
182d | -0.746* [0.116] | 1.09* [0.124] | 0.434 | 0.674 |
注:*表示在5%水平下拒绝原假设;方括号内为Newey-West标准差;Wald检验项内为相应的P值
三、时变的期限风险溢价
较短期限的利差β系数在0与1之间,提示我们从时变的期限风险溢价进行考察或许对于解释交易所国债回购市场的利率期限结构变化有一定的帮助。Mankiw和Miron(1986)[8]证明了在时变的期限风险溢价条件下,式(6)的β系数估计值变为:
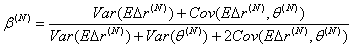 (7)
(7)
式(7)表明,若期限风险溢价的方差为0(意味着期限风险溢价与预期利率变化的协方差为0),β系数则为0。然而,若存在一个时变的风险溢价,则协方差的变化在一定范围内时,β系数将会介于0与1之间,即前面我们得到的结果。
为得到时变的期限风险溢价,在此我们借鉴Stefan Gerlach(2003)的方法,使用7天期利率的响应方差对数值log(σ2t)作为期限风险溢价的替代,进而将式(6)变换为:
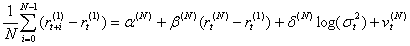 (8)
(8)
其中δ表示期限风险溢价的影响。由于σ2t无法直接得到,我们通过GARCH(1,1)模型得到7天回购利率变动的方差(Stefan Gerlach),并将其对数值作为期限风险溢价的替代变量:

四、时变的期限风险溢价下的预期理论检验
通过GMM方法对式(8)进行预期理论的检验,结果见表3。从表中结果可见, 14天和28天利差的检验方程的拟合优度有了显著的提高,总体上各期限利率差的检验方程的拟合结果有了改善。14天期利差的检验方程中,期限溢价的γ系数仍不显著,即利差不存在明显的期限溢价,但β系数的Wald检验表明不能拒绝β=1的原假设;28天期利差的检验方程中,γ系数显著为负,表明考虑了时变的期限风险溢价条件下,式(8)右边的各因素均对预期有显著影响,且解释力度提高;91天、128天利差检验方程的β系数、γ系数均显著异于0,且Wald检验结果与表2相同,不能拒绝β=1的原假设。因此,当考虑了时变的期限风险溢价时,各期限利差的实证结果支持利率期限结构的预期理论。
表3 时变的期限风险溢价条件下GMM对预期理论的检验
利率期限 | α(N) | β(N) | γ(N) | Wald检验 |
|
14d | -0.026 [0.017] | 0.669* [0.118] | -0.010 [0.023] | 0.375 | 0.364 |
28d | -0.052 [0.060] | 0.776* [0.245] | -0.121* [0.059] | 0.360 | 0.473 |
91d | -0.466* [0.084] | 0.974* [0.184] | -0.186* [0.048] | 0.888 | 0.778 |
182d | -0.718* [0.092] | 0.846* [0.144] | -0.292* [0.059] | 0.309 | 0.725 |
结论
本文对上海证券交易所国债回购市场的利率期限结构进行了实证研究,发现与之前国内学者的研究结果有所不同,在亚洲金融危机过后,虽然利率期限结构不能由传统的预期理论来解释,但是通过进一步研究,发现存在时变的期限风险溢价,当把这一重要因素纳入实证范围中时,检验结果支持了利率期限结构的预期理论。
另外,从最终结果来看,14天、28天利差的检验方程拟合优度仍不到50%,因此,即期短期利差对于未来利率变动仅具有部分解释力度,若用来预测将来的利率变化,还需要考虑到其他因素的影响,如市场流动性、投资者对于未来市场风险的判断等等。
值得注意的是,目前我国的国债市场不但从组织结构上被分割成交易所债券市场、银行间债券市场和柜台市场;而且,每个市场中的产品特点、投资者特征有着明显的区别,使得交易所市场的国债回购利率不能代表整个证券市场的资金价格:第一,从投资主体构成来看,在交易所债券市场中的主要参与主体是保险公司、证券公司、基金公司、投资公司、等;银行间市场的主要参与主体是商业银行、农信社、保险公司、证券公司等。第二,投资者需求特征也是截然不同的,例如保险公司主要偏重于长期债券,国有银行和股份制银行需求偏好较为丰富,但是明显表现在对中短期品种的偏好;基金公司明显偏好短期债券;证券公司等其他机构受到资金影响,并不是最主要的长期投资者。第三,从交易动机来看,保险公司更多的是买入持有到期的策略,交易并不积极。由于市场分割和投资偏好割裂,使得交易所市场与银行间市场的国债回购利率表现出不同的特征。这一方面使得国债二级市场利率缺乏联动性,另一方面也削弱了公开市场操作对货币供给量与市场利率的引导和调节力度。
人民银行、财政部和证监会等市场管理者从货币政策及财政政策的贯彻实施以及资本市场的长期考虑,已经认识到市场分割带来的许多难以克服弊端,表现出对市场统一的关注。为促进我国债券市场的统一,有关主管部门已采取了一系列措施:2002年4月15日,银行间市场开放;同年11月27日,第一支真正意义上的跨市场国债020015券发行和交易;自2004年以来,基准利率国债实行全部跨市场发行。
笔者认为,随着跨市场品种和转托管数量的增多,跨市交易者队伍的扩大,这对树立基准利率国债在国债市场上主流品种地位、为市场提供利率基准、构建基准国债利率体系、完善收益率曲线和加速银行间市场和交易所市场的统一进程等方面起到了一定的作用。目前,我国的国债回购市场还很不成熟,利率的市场形成机制还不完善,我们必须从培育市场交易主体、丰富市场交易品种、多大市场交易规模、完善市场管理与制度建设等多方面入手,加快货币市场发展,提高回购市场运行效率,逐步建立起我国市场利率的有效形成机制。